|
Задача 1. «Одиниці»
Умова. Дано ціле число I записане в десятковій системі числення.
Завдання. Написати програму ONE.*, яка порахує кількість одиниць в його двійковому записі.
Вхідні дані. Вхідний текстовий файл ONE.DAT містить в єдиному число I.
Вихідні дані. Вихідний текстовий файл ONE.SOL містить єдине ціле число - кількість одиниць.
Приклади файлів
Задача 2. «Нафтові плями»
Умова. Після аварії на морській нафтовій свердловині в океан вилилося багато нафти. Вона розтеклася по воді, після чого утворилася певна кількість нафтових плям. Для ліквідації наслідків аварії було створено штаб з координації дій. Співробітники штабу зберігають інформацію про плями в комп'ютері у вигляді матриці розмірністю M x N. Комірка матриці містить 0, якщо нафтова пляма в цих координатах відсутня та 1, якщо наявна (2 ≤ M, N ≤ 100). У матриці комірки плям не можуть дотикатися одна до одної ні сторонами, ні кутами.
Приклади файлів
|
1
|
0
|
1
|
0
|
0
|
|
0
|
0
|
1
|
1
|
0
|
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
0
|
1
|
|
1
|
0
|
1
|
0
|
1
|
|
OIL.DAT
|
OIL.SOL
|
|
5 5
1 0 1 0 0
0 0 1 1 0
1 0 0 0 0
1 0 0 0 1
1 0 1 0 1
|
5
1 2
2 1
3 2
|
Завдання. Для полегшення ліквідації наслідків аварії потрібно написати програму OIL.*, яка знаходитиме загальну кількість плям та кількість плям з однаковою площею.
Вхідні дані. Вхідний текстовий файл OIL.DAT містить в першому рядку два числа M та N, далі слідують M рядків, у кожному по N цілих чисел розділених пропусками - елементи матриці.
Вихідні дані. Вихідний текстовий файл OIL.SOL містить у першому рядку ціле число k - загальну кількість плям, далі у кожному з рядів міститься по два числа, перше - площа плями, друге - їх кількість. Дані посортувати по площах в порядку зростання.
Завдання 3. «Ламана»
Ім'я файлу програми: LAMAN.*
Ім'я вхідного файлу: LAMAN.DAT
Ім'я вихідного файлу: LAMAN.SOL
Максимальний час роботи на одному тесті: 5с
Шоколадна плитка являє собою сітку з горизонтальних та вертикальних ліній, точки якої в декартовій системі координат на площині позначено точками з цілими координати. Потрібно поділити шоколадну плитку наступним чином:
- починати з лівого нижнього кута, який знаходиться в початку координат;
- можна пересуватися вздовж цих прямих;
- при проходженні через точку завжди змінювати напрям швидкості на перпендикулярний.
Знайти мінімальну довжину шляху до верхньої правої точки.
Технічні умови. Програма Laman читає з файлу розміри шоколадної плитки (цілі числа, не більші 10^100000). Числа розділено пропуском. Програма виводить на екран єдине число - шукану величину.
Приклади файлів
|
LAMAN.DAT
|
LAMAN.SOL
|
|
2 3
|
5
|
Задача 4. Сума дільників
Ім'я вхідного файлу: sum.in
Ім'я вихідного файлу: sum.out
Нехай х - натуральне число. Назвемо число y його дільником, якщо 1 ≤ у ≤ х і залишок від ділення x на y дорівнює нулю.
Задано число х. Знайдіть суму його дільників.
Формат вхідних даних: перший рядок вхідного файлу містить одне ціле число х (1 ≤ х ≤ 1018). Усі прості дільники числа х не перевищують 1000.
Формат вихідних даних: єдиний рядок вихідного файлу має містити одне число - суму дільників заданого числа х.
Приклад вхідних і вихідних даних:
|
sum.in
|
sum.out
|
|
12
|
28
|
|
239
|
240
|
Задача 5. Куфічний дирхем
|
Вхідний файл
|
dirkhem.in
|
|
Вихідний файл
|
dirkhem.out
|
Віталій Вікторович завжди був комунікабельною людиною і, відповідно, мав багато друзів. Одного вечора, переглядаючи свою електрону пошту, він був приємно здивований запрошенням на ювілей свого студентського друга Шаміля Ігоровича і одразу ж прийняв позитивне рішення.
Дізнавшись, що Шаміль Ігорович вже багато років захоплюється колекціонуванням старовинних монет і полює за середньовічною срібною монетою з назвою «Куфічний дирхем», Віталій Вікторович вирішив неодмінно подарувати йому цю монету.
Скориставшись Інтернетом, Віталій Вікторович визначив всі K міст, де можна придбати дану монету, а також її вартість у кожному із цих міст. Країна, у якій живуть Віталій Вікторович і Шаміль Ігорович, налічує N міст і M двосторонніх автомобільних доріг, кожна з яких з'єднує два різних міста держави. Відомо, що Віталій Вікторович живе в місті A, а Шаміль Ігорович - в місті B. Для кожної дороги Віталій Вікторович обчислив вартість проїзду з урахуванням технічних характеристик свого автомобіля. З метою економії Віталій Вікторович вирішив придбати монету по дорозі із міста A у місто B. Іншими словами, маршрут руху Віталія Вікторовича повинен проходити через місто, у якому він вирішить придбати монету. Однак виявилось, що їхати через місто, у якому монета коштує менш за все, не завжди вигідно, тому що вигравши у вартості монети, можна втратити набагато більше у вартості дороги і навпаки...
Ваше завдання - допомогти Віталію Вікторовичу вибрати оптимальний маршрут і місто Z, де слід придбати монету. Маршрут повинен починатися в місті A, закінчуватися в місті B і проходити через місто Z. Вартість даного маршруту повинна бути мінімальною. Під вартістю маршруту будемо розуміти суму кількості грошей, витрачених на дорогу і вартість монети в місті Z. Нижче наведено приклад для N = 5, M = 7, A = 1, B = 4.
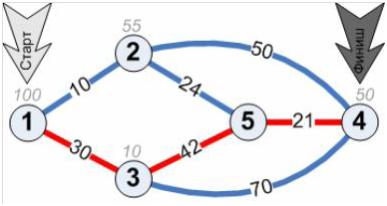
Рисунок 1.Візуалізація другого прикладу.
Для даного приклада K = 4, вартість монети позначено зверху над кругом, що позначає місто.
Оптимальний маршрут виділено червоним кольором. Для даного прикладу Z = 3.
Вхідні дані:
Перший рядок вхідного файлу містить три цілих числа N, M і K (2 ≤ N ≤ 5000; 1 ≤ M ≤ 100000; 1 ≤ K ≤ N), де N - кількість міст в країні, M - кількість доріг, а K - кількість міст, у яких продається шукана монета. Будемо вважати, що всі міста пронумеровані цілими числами від 1 до N.
Другий рядок вхідного файлу містить два цілих числа A і B (1 ≤ A, B ≤ N; A ≠ B), де A - номер міста, в якому живе Віталій Вікторович, а B - номер міста, в якому живе Шаміль Ігорович.
Третій рядок містить K пар цілих чисел Vi і Сi( 1 ≤ Vi ≤ N; 1 ≤ Сi ≤ 109), де Vi - це номер міста, у якому можна придбати потрібну монету, а Сi - вартість монети у відповідному місті. Відомо, що Vi ≠ Vj, якщо i ≠ j. Всі числа у рядку розділені одиночними пробілами.
Кожен наступний із M рядків містить три числа Xi, Yi, Si (1 ≤ Xi, Yi ≤ N; Xi ≠ Yi; 1 ≤ Si ≤ 105), де Xi і Yi - номери міст, з'єднаних двосторонньою дорогою, а Si - вартість проїзду по даній дорозі. Не існує двох різних доріг, що з'єднують одні і ті ж міста.
Вихідні дані
Єдиний рядок вихідного файлу має містити одне ціле число - мінімальну вартість маршруту. Гарантується, що рішення існує.
Приклад вхідних та вихідних даних:
|
dirkhem.in
|
dirkhem.out
|
Маршрут, город Z
|
|
3 3 2
3 1
1 20 2 5
1 2 7
1 3 5
2 3 8
|
20
|
{3, 2, 1}
Z = 2
|
|
5 7 4
1 4
1 100 4 50 3 10 2 55
1 2 10
5 3 42
1 3 30
2 4 50
3 4 70
2 5 24
4 5 21
|
103
|
{1, 3, 5, 4}
Z = 3
|
|
8 7 1
1 6
5 187
1 8 32
8 6 39
5 4 51
1 4 101
2 4 17
3 7 46
2 8 23
|
440
|
{1, 8, 2, 4, 5, 4, 2, 8, 6}
Z = 5
|
|