|
Динамічне прогамування на графах |
 |
 |
 |
|
Добавил(а) Administrator
|
|
11.03.11 13:40 |
|
(динамічне програмування)
Найкоротші шляхи
Нехай є n міст, пронумерованих числами від 1 до n. Для кожної пари міст із номерами і, j у таблиці a[і][j] зберігається ціле число - ціна прямого авіаквитка з міста i у місто j. Вважається, що рейси існують між будь-якими містами, a[і,і] = 0 при всіх і, a[і][j] може відрізнятися від a[j,і]. Найменшою вартістю проїзду з і в j вважається мінімально можлива сума цін квитків для маршрутів (у тому числі з пересадженнями), що ведуть з і в j. (Вона не перевершує a[і][j], але може бути менше).
У пропонованих нижче задачах потрібно знайти найменшу вартість проїзду для деяких пар міст при тих чи інших обмеженнях на масив a і на час роботи алгоритму.
Припустимо, що не існує замкнутих маршрутів, для яких сума цін негативна. Передбачається, що ця умова (відсутність циклів з негативною сумою) виконана.
1) Знайти найменшу вартість проїзду з 1-го міста в усі інші .
Позначимо через Мінвар(1,s,к) найменшу вартість проїзду з 1 у s менш чим з k пересадженнями. Тоді виконується таке співвідношення:
Мінвар (1,s,k+1) = найменшому з чисел Мінвар(1,s,k) і
Мінвар(1,і,k) + a[і][s] (і=1..n)
Як відзначалося вище, шуканою відповіддю є Мінвар (1,і,n) для всіх і=1..n.
((0,20,3,4,5,6),
(20,0,5,6,7,8),
(3,5,0,6,7,8),
(4,6,6,0,8,8),
(5,7,7,8,0,9),
(6,8,8,8,9,0));
1 2 -----20
1-3 ---- 3 , 3-2---- 5= 8
min(20,8)=8
флойд
for k:=1 to n do
for i:=1 to n do
for j:=1 to n do
if a[i,k]+a[k,j] a[i,j]:=a[i,k]+a[k,j];
Практична робота: «Визначення найкоротшого шляху в графі методом динамічного програмування»
Прізвище ______________________________
|
№
|
Завдання
|
Результат
|
|
1.
|
Намалювати граф з кількістю вершин N=6
(навантажений, неорієнтований)
|
|
|
2.
|
Написати матрицю суміжності
Зауваження, якщо немає зв’язку, то записати велике число, наприклад 1000
|
|
|
3.
|
Намалювати каркас мінімальної ваги (остове дерево)
|
|
|
4.
|
Скопіювати папку «!Лабораторна 10 динамічне» в свою папку
Занести матрицю в файл graph.dat
|
|
|
5.
|
За допомогою програми ford.dpr відшукати всі мінімальні шляхи та занести в таблицю
|
|
|
6.
|
За допомогою програми floid.dpr відшукати всі мінімальні шляхи та занести в таблицю
|
|
|
7.
|
За допомогою програми deikstr.dpr відшукати всі мінімальні шляхи з вершини start в вершину finish та занести в таблицю
|
|
|
№
|
Start
|
Finish
|
Шлях
|
Довжина
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
5
|
|
|
|
|
|
6
|
|
|
|
|
|
8.
|
Порівняти результати таблиць в завданнях 5,6,7
|
|
|
|
|
|
|
|
|
|
|
|
Добавил(а) Administrator
|
|
11.10.16 09:53 |
|
Заняття 3 (21.09.2016)
Завдання 1
Дано послідовність з N чисел, котра містить різні числа від 0 до N. Визначити, якого числа не існує в даній послідовності.
Завдання 2
- https://www.e-olymp.com/uk/problems/192
- http://nvk26.lutsk.ua/cgi-bin/new-client?contest_id=24 (завдання B )
Логін school2016-1 . . . school2016-10 (пароль - 1)
Хтось вмістив пару новонароджених кроликів в деякому місці, обгородженому з усіх боків стіною. Скільки пар кроликів народиться при цьому протягом року, якщо природа кроликів така, що кожний місяць, починаючи з третього місяця після свого народження, пара кроликів породжує іншу пару?
Використаємо рекурентну формулу чисел Фібоначі.
Кожне число Фібоначі знаходять за формулою:
Додаток
1. Волинська учнівська Інтернет-олімпіада з програмування у 2016-2017 н. р. http://93.183.238.10/vippoolimp/.
2. Повідомляємо, що а сайті http://netoi.org.ua (http://www.olymp.vinnica.ua) почалася реєстрація учасників відкритої Всеукраїнської Інтернет-олімпіади з інформатики NetOI-2016
3. Школа з програмування (м. Київ)
Природничо-науковий ліцей №145 оголошує про початок роботи Київської школи олімпійського резерву з програмування. Мета школи – підготовка учнів міста Києва до олімпіад з інформатики (програмування) різних рівнів. Перше (організаційне) заняття відбудеться 24 вересня. Заняття цілком безкоштовні!
https://itolymp.com/
4. Інтелектуальні змагання школярів в мережі Інтернет.
Сервіс підтримки Інтернет-олімпіади з інформаційних технологій ІОІТ-2016
5. ІОІТ 2017
Відповідно до Положення про Всеукраїнські учнівські Інтернет-олімпіади, затвердженого наказом Міністерства освіти і науки, молоді та спорту України від 11 червня 2012 року № 671, зареєстрованого в Міністерстві юстиції України 27 червня 2012 року за № 1074/21386, наказу Міністерства освіти і науки України від 07.06.2016 №626 «Про проведення Всеукраїнських учнівських Інтернет-олімпіад з математики, фізики, хімії, біології, географії, економіки, інформатики, інформаційних технологій у 2016/2017 навчальному році» Міністерством освіти і науки України, Київським національним університетом імені Тараса Шевченка спільно зУкраїнським фізико-математичним ліцеєм КНУ імені Тараса Шевченка розпочато проведення Всеукраїнської учнівської Інтернет-олімпіади з інформаційних технологій у 2016/2017 навчальному році.
Всеукраїнська учнівська Інтернет-олімпіада проводиться у два етапи в наступні терміни:
І ( заочний) етап:30 червня – грудень 2016 року;
ІІ (очний) етап:січень – лютий 2017 року.
Реєстрація для участі в олімпіаді відбувається за цимпосиланням.
Ознайомитися із умовами реєстрації та етапами проведення олімпіади можна за посиланнямhttp://upml.knu.ua/internet-olimpiada-it-2017/
|
|
Читать полностью
|
|
|
Розбір задач 1-4 (заняття 1 ---03.10.20112) |
 |
 |
 |
|
Добавил(а) Гісь Ігор Володимирович
|
|
12.10.12 19:13 |
|
Програми розв'язку task1, task2_1, task2_2, task3_1, task3_2, task3_3, task4
Тести для перевірки test1, test2, test3, test4
Повторення базові структури алгоритмів
|
Задача 1.
Обчислити суму, різницю та добуток двох введених чисел.
|
Задача 2.
Перевірити правильність виразу
a o b = c
за заданими трьома числами a, b, c та операцією o(+ - *).
|
Задача 3.
Для заданого N знайти всі значення виразу
a o b о c, де
a, b, c натуральні числа <=N операцією o(+ - *).
|
|
#include "stdafx.h"
#include "iostream"
using namespace std;
int _tmain()
{
int a,b,s,r,d;
cin>>a>>b;
s=a+b;
r=a-b;
d=a*b;
cout<<s<<"\n";
cout<<r<<endl;
cout<<d<<endl;
return 0;
}
|
#include "stdafx.h"
#include "iostream"
using namespace std;
int _tmain()
{
int a,b,c;
char o;
cin>>a>>b>>c;
cout<<"+ - * ";
cin>>o;
if ((o=='+' && a+b==c)||(o=='-' && a-b==c)||(o=='*' && a*b==c))
cout<<a<<o<<b<<"="<<c<<"\n";
else
cout<<a<<o<<b<<"<>"<<c<<"\n";
return 0;
}
|
#include "stdafx.h"
#include "iostream"
using namespace std;
int _tmain()
{
int n,a,b,c,r;
cin>>n;
for (a=1;a<=n;a++)
for (b=1;b<=n;b++)
for (c=1;c<=n;c++)
{
r=a+b+c; cout<<a<<"+"<<b<<"+"<<c<<"="<<r<<endl;
r=a+b-c; cout<<a<<"+"<<b<<"-"<<c<<"="<<r<<endl;
r=a+b*c; cout<<a<<"+"<<b<<"*"<<c<<"="<<r<<endl;
r=a-b+c; cout<<a<<"-"<<b<<"+"<<c<<"="<<r<<endl;
r=a-b-c; cout<<a<<"-"<<b<<"-"<<c<<"="<<r<<endl;
r=a-b*c; cout<<a<<"-"<<b<<"*"<<c<<"="<<r<<endl;
r=a*b+c; cout<<a<<"*"<<b<<"+"<<c<<"="<<r<<endl;
r=a*b-c; cout<<a<<"*"<<b<<"-"<<c<<"="<<r<<endl;
r=a*b*c; cout<<a<<"*"<<b<<"*"<<c<<"="<<r<<endl;
}
return 0;
}
|
|
Задача 4
Для задачі 3 знайти значення результату, яке повторюється найбільше
|
Обчислити факторіал
|
|
#include "stdafx.h"
#include "iostream"
using namespace std;
int _tmain()
{
int n,a,b,c,r[1000];
cin>>n;
int k=0;
//заповнення масиву результатів
for (a=1;a<=n;a++)
for (b=1;b<=n;b++)
for (c=1;c<=n;c++)
{ k++;r[k]=a+b+c; k++;r[k]=a+b-c; k++;r[k]=a+b*c; k++;r[k]=a-b+c; k++;r[k]=a-b-c; k++;r[k]=a-b*c; k++;r[k]=a*b+c; k++;r[k]=a*b-c;
k++;r[k]=a*b*c; }
//Сортування масиву
int i,j,temp;
for (i=1;i<=k;i++)
for (j=1;j<=k;j++)
if (r[i]<r[j]) {temp=r[i];r[i]=r[j];r[j]=temp;}
//Вивведення масиву
//for (i=1;i<=k;i++)cout<<r[i]<<" ";cout<<"\n";
//пошук кількості сусідніх однакових елементів
int k1,k2,el;
k1=1;k2=0;
for (i=1;i<k;i++)
if (r[i]==r[i+1]) {k1++;}
else {if (k1>k2){k2=k1;el=r[i];}
k1=1;}
cout<<el<<" "<<k2<<endl;
return 0;
}
|
#include "stdafx.h"
#include "iostream"
using namespace std;
int _tmain()
{
int i,n;
int f[1000];
cin>>n;
f[0]=1;
for (i=1;i<=n;i++)
{f[i]=f[i-1]*i;
cout<<i<<"!="<<f[i]<<endl;
}
return 0;
}
|
|
|
Добавил(а) Administrator
|
|
11.03.11 13:34 |
|
Жадібні алгоритми на графах
Жадібний алгоритм - метод оптимізації задач, заснований на тому, що процес ухвалення рішення можна розбити на елементарні кроки, на кожному з яких ухвалюється окреме рішення.
Рішення приймається на кожному кроці повинне бути оптимальним тільки на поточному кроці і повинне прийматися без урахування попередніх або подальших рішень.
Ознаки того, що задачу можливо вирішити за допомогою жадібного алгоритму:
1. Задачу можна розбити на підзадачі;
2. Величини, що розглядаються в задачі, можна дробити так само як і задачу на підзадачі;
3. Сума оптимальних рішень для двох підзадач дасть оптимальне рішення для всієї задачі.
Приклад задачі
Пасажирський ліфт не може підняти більше W кг. В ліфт намагаються влізти H людина, причому для кожного з них відома його вага: W1, W2 ... WH. Визначити яку максимальну кількість людей зможуть виїхати на ліфті за один раз.
Рішення
Очевидно, що елементарною підзадачею є приміщення в ліфт однієї людини. Якщо є декілька кандидатів на приміщення в ліфт, то оптимальним вибором буде людина з якнайменшою вагою, оскільки при цьому залишається найбільший запас по вантажопідйомності.
Тому, для вирішення задачі, відсортуємо людей по їх вазі і будемо, починаючи з найлегшим, поміщати їх в ліфт, поки це ще можна зробити.
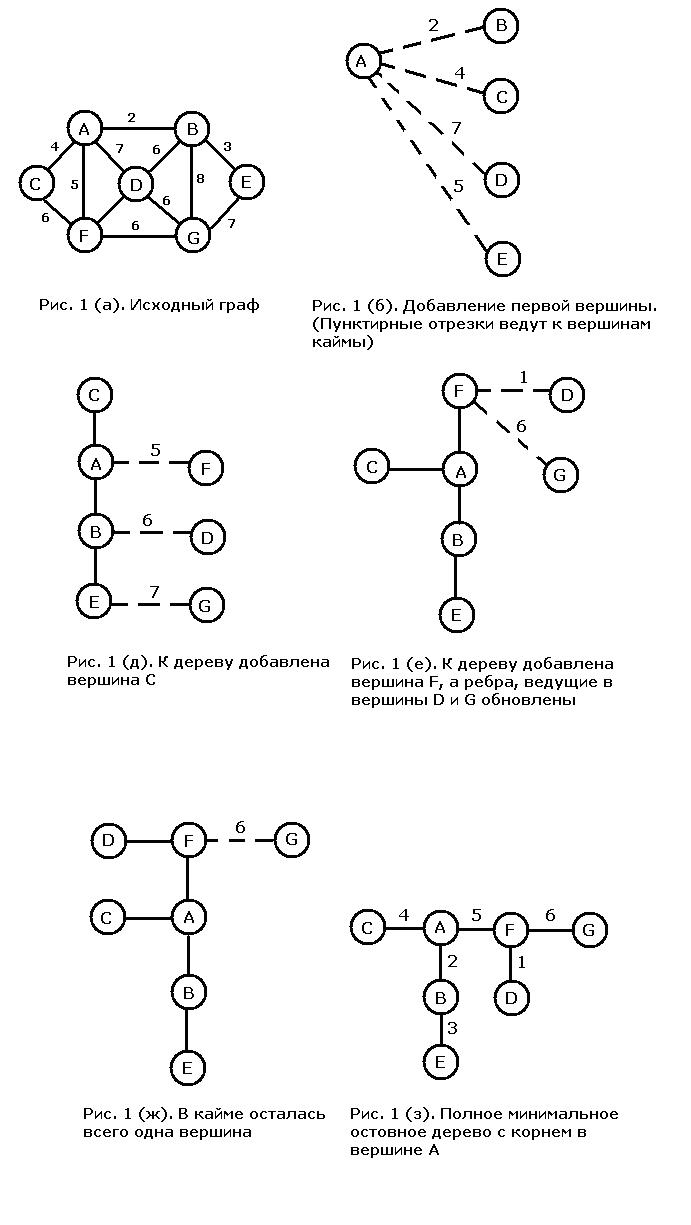
Алгоритм пошуку мінімального остового дерева
Алгоритм Дейкстри-Прима
|
|