|
Добавил(а) Administrator
|
|
11.10.16 10:00 |
|
Заняття 5 (05.10.2016)
Базові структури алгоритмів (структура циклу)
1. Прості числа
http://www.e-olymp.com/uk/problems/830
Вивести всі прості числа від M до N включно.
Вхідні дані
У першому рядку знаходяться відокремлені пропуском M і N (2 ≤ M ≤ N ≤ 300 000).
Вихідні дані
Вивести числа у порядку зростання, по одному у рядку. Якщо між M і N включно немає простих - вивести "Absent" (без лапок).
Вхідні дані
Sample 1
2 5
Sample 2
4 4
Вихідні дані
Sample 1
2
3
5
Sample 2
Absent
2. Решето Ератосфена
http://www.e-olymp.com/en/problems/4739
За введеним числам A і B вивести всі прості числа в інтервалі від A до B включно.
Вхідні дані
У єдиному рядку вводяться два числа 1 ≤ A≤ B≤ 100000.
Вихідні дані
Вивести в один рядок всі прості числа в інтервалі від A до B включно.
Input example
Sample 1
2 2
Sample 2
1 100
Output example
Sample 1
2
Sample 2
$12 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
3.Codeforces (http://codeforces.com/)
http://codeforces.com/problemset/problem/550/A
Два підрядки
Дано рядок s. Потрібно визначити, чи існують в цьому рядку s два непересічні підрядка "AB" і "BA" (ланцюжки можуть йти в будь-якому порядку).
Вхідні дані
На вхід подається рядок s довжиною від 1 до 105 символів, що складається з великих літер латинського алфавіту.
Вихідні дані
Виведіть "YES" (без лапок), якщо рядок s містить дві непересічні підрядка "AB" і "BA", і "NO" інакше.
приклади тестів
вхідні дані
ABA
вихідні дані
NO
вхідні дані
BACFAB
вихідні дані
YES
вхідні дані
AXBYBXA
вихідні дані
NO
Примітка
У першому прикладі вхідних даних, незважаючи на те, що є підрядка "AB" і "BA", їх входження перетинаються, тому відповідь - "NO".
У другому прикладі вхідних даних є наступні входження подстрок: BACFAB.
У третьому прикладі немає ні підрядка "AB", ні підрядка "BA".
|
|
Читать полностью
|
|
Добавил(а) Гісь Ігор Володимирович
|
|
19.10.12 14:50 |
|
Трикутник
Трикутник – 1) багатокутник із трьома сторонами; 2) це фігура, що складається з трьох точок, які не лежать на одній прямій, та трьох відрізків, які сполучають попарно ці точки. Відрізки називають сторонами трикутника, а точки – вершинами трикутника.
Бісектриса трикутника – відрізок бісектриси кута, що з'єднує вершину трикутника з точкою протилежної сторони. Довжину бісектиси трикутника, ака проведена до сторони a, можна знайти за формулою la=2/(a+b)*sqrt(b*c*p*(p-1)), p=(a+b+c)/2
Медіана трикутника – відрізок, який з'єднує вершину трикутника з серединою протилежної сторони. Довжину медіани трикутника, ака проведена до сторони a, можна знайти за формулою ma=sqrt(2*a^-+2*c^2-a^2)
Висота трикутника – перпендикуляр, проведений із вершини трикутника до прямої, що містить протилежну сторону. Довжину висоти трикутника, ака проведена до сторони a, можна знайти за формулою:ha=2s/a.
Периметр трикутника p=a+b+c; a=sqrt((x2-x1)^2+(y2-y1)^2); b=sqrt((x3-x2)^2+(y3-y2)^2); c=sqrt((x1-x3)^2+(y1-y3)^2).
Площа трикутника дорівнює півдобутку сторони на висоту, проведену до цієї сторони:Формула: S=a*h/2
Площа трикутника дорівнює півдобутку сторін на синус кута між ними:Формула: S=b*c*sin(α)/2
Площа трикутника (формула Герона) дорівнює Формула: S=sqrt(p*(p-a)*(p-b)*(p-c)),p=(a+b+c)/2
Площа трикутника (векторний добуток) s=1/2|(x1*y2-x2*y1)+(x2*y3-x3*y2)+(x3*y1-x1*y3)|
Радіус кола, описаного навколо трикутника: Формула: r=abc/4S
Радіус кола, вписаного в трикутник:Формула: r=S/p
Теорема косинусів Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.Формула: a^2 = b^2 + c^2 - 2*b*c*cos(alpha)
Теорема синусів Сторони трикутника пропорційні синусам протилежних кутів.Формула: a/sin(alpha) = b/sin(beta) = c/sin(gamma)
Теорема Піфагора. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів його катетів, тобто c^2 = a^2 + b^2
Задачі
Рівень 1
1.За заданими сторонами обчислити периметр трикутника.
2. За заданими координатами точок обчислити периметр трикутника.
3. За заданими сторонами обчислити площу трикутника.
4. За заданими координатами точок обчислити площу трикутника.
5. За заданими сторонами перевірити чи є трикутник рівностороннім.
6. За заданими сторонами перевірити чи є трикутник рівнобедреним.
7. За заданими координатами точок визначити чи є трикутник прямокутним.
8. Перевірити існування трикутника з заданими сторонами.
Рівень 2
1. За заданими координатами вершин трикутника обчислити його висоти.
2. Трикутник на площині задається цілочисельними координатами вершин. Для заданої точки Z(x,y) визначити, чи належить вона стороні трикутника чи лежить усередині чи поза ним.
3. В межах міста, границя якого відома, а будинки задані своїми координатами, потрібно вибрати місце для будівництва хімічного заводу так, щоб відстань від нього до найближчого будинку була максимальною. Фактично нам потрібно знайти коло з максимальним радіусом, яке не має всередині точок з початкової множини, центр якого лежить всередині або на границі заданої ламаної.
4. За координатами будівель міста підібрати місце для будівництва культурного центру так, щоб відстань до максимально віддаленого від нього будинку була мінімальною.
Додатковий матеріал
1. Структура розгалуження С++
2. Обчислювальна геометрія (Омелян П.П.)
|
|
Последнее обновление 19.10.12 14:55 |
|
|
Завдання з теми Теорія графів |
 |
 |
 |
|
Добавил(а) Administrator
|
|
11.03.11 13:48 |
|
Прізвище ______________
Завдання на міні-олімпіаду
1. За заданими малюнком (20 балів)
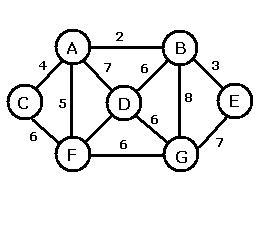
а) задайте матрицю суміжності
б) знайти ейлеровий шлях; _________________________________________________
в) знайти гамільтонів шлях; ________________________________________________
г) знайти найкоротший гамільтонів шлях; ____________________________________
г) написати програму, яка за описаним графом, виводила довжину ейлеревого шляху, якщо він існує, якщо шлях не існує виводить повідомлення NO.
д) написати алгоритм пошуку та виведення всіх шляхів з вершини I вершину J для графу заданого на малюнку вище.
2. Задача 1. (30 балів , алгоритм Флойда)
Вхідні дані задані у файлі Graph.dat у вигляді 1 рядок – N – кількість ребер, M – кількість вершин (M<=100, N<=10000) , наступні N рядків задають і, j вершини і довжину ребра aij (aij<=10000). У файл Graph.sol вивести найкоротшу довжину з вершини I в вершину J в форматі I J Dij, та повідомлення NO, якщо шляху не існує.
|
Graph.dat
|
Graph.sol
|
|
12
1 2 2
2 7 3
7 6 7
6 5 6
5 3 6
3 1 4
1 5 5
1 4 7
5 4 1
2 4 6
6 4 6
2 6 8
|
1 2 2
1 3 4
1 4 6
1 5 5
1 6 10
1 7 5
2 3 6
2 4 6
2 5 7
2 6 8
2 7 3
3 4 7
3 5 6
3 6 12
3 7 9
4 5 1
4 6 6
4 7 9
5 6 6
5 7 10
6 7 7
|
3. Задача 2. (50 балів , алгоритм Прима)
Збирання мита.
Король країни Аріїв завоював N міст на території сусідніх держав.
Тепер йому необхідно створити систему збирання мита з завойованих територій. Він хоче збудувати таку систему шляхів між цими містами, щоб до будь-якого міста можна було дістатися (можливо, через інші міста) зі столиці, але у воєнному стані на транспорт виділяється дуже незначна частина фінансів, тому сумарна вартість побудованих шляхів сполучення між містами має бути мінімальною.
Вхідні дані:
Перший рядок вхідного файлу містить натуральне число N (1<=N<=100) – кількість міст у країні, а також цілі числа X та Y – координати столиці.
Наступні N рядків містять через проміжок координати Xi , Yi завойованих міст.
Значення координат по модулю менші 50000.
Вихідні дані:
Перший рядок має містити дійсне число з трьома знаками після коми – сумарну вартість побудованих доріг. Вважайте, що вартість одиниці довжини дороги дорівнює одній умовній одиниці.
Наступні рядки мають містити у довільному порядку список побудованих доріг у форматі: =>
При цьому столицю позначте номером 0. Якщо відповідей декілька, виведіть одну довільну з них. Приклади:
|
TALLAGE.DAT
|
TALLAGE.SOL
|
|
6 0 0
1 1
-1 1
0 2
1 -1
-1 -1
0 -2
|
8.485
2 3
3 1
1 0
0 4
4 6
6 5
|
Додаткова задача.
4. Відомий всім форт Буайяр пропонує своїм відвідувачам таке випробування: піднятися по досить нахиленій слизькій площині вгору, щоб дістати ключ. На площині розміщені невеличкі виступи, кожний виступ настільки малий, що поміститися на ньому може лише одна нога. Домовимося, що під час пересування по площині гравець не може перехрещувати ноги (ліву за праву і навпаки). Нехай L максимальна довжина кроку гравця, п — кількість виступів, (хi; yj)і = 1,2, ..., п — координати виступів на площині.
Вважатимемо, що початкове положення гравця: х0 > О, у0 = 0 (стартує з будь-якого місця на підлозі).
Визначте всі можливі найменші за кількістю кроків варіанти (якщо вони існують) послідовностей номерів виступів, по яких необхідно рухатись гравцю, чергуючи ноги, щоб дістатися самого верхнього виступу. Вкажіть, з якої ноги йому починати рух. Всі вхідні дані вважати цілими числами.
|
|
17.09.2014 Розв'язки задачі "Відрізок" |
 |
 |
 |
|
Добавил(а) Administrator
|
|
06.10.14 10:39 |
|
Розв’язання
Розглянемо найпростіший алгоритм розв’язання задачі. Перебиратимемо всі трійки відрізків.
Для кожної трійки треба перевірити можливість існування відповідного трикутника. Якщо трикутник існує, підрахуємо сумарну вартість трьох відрізків, а з усіх знайдених вартостей виберемо найменшу. Складність алгоритму — N(N3).
А от швидше розв’язання. Розглядатимемо всі відрізки в порядку від найкоротших до найдовших і підтримуватимемо таку структуру даних: масив F, у комірці F[C] якого зберігається найбільша сумарна довжина двох відрізків (з числа перших N відрізків) із загальною вартістю c. Оскільки ціни відрізків не перевищують N, сумарна вартість двох відрізків не буде більшою за 2N. Переходячи до чергового ((k + 1)-го) відрізка — нехай цей відрізок має довжину L та вартість C — ми шукаємо найменше таке значення c, для якого F[c] >L. Це можна зробити простим лінійним пошуком. Для знайденого значення c сума C + c буде найменшою можливою вартістю трикутника, найбільшою стороною якого є розглядуваний відрізок. Якщо ця сума менша за поточний мінімум знайдених вартостей, відповідним чином цей мінімум оновлюємо. Крім того, оновлюємо і сам масив F[c]. Для цього пробуємо взяти в пару з (k + 1)-м відрізком почергово всі відрізки від першого до k-го і оновлюємо, якщо потрібно, відповідну комірку масиву F. Таким чином, на кожному з N кроків ми виконуємо з N кроків ми виконуємо O(N) операцій, тож загальна складність алгоритму — O(N2).
Тепер розглянемо оптимальне розв’язання. Воно базується на такій нескладній властивості:
Властивість. Якщо серед натуральних чисел L1, L2, ..., Lk немає трьох таких, що утворюють сторони трикутника, то найбільше з цих чисел не може бути меншим за K-й член послідовності Фібоначчі. Послідовність Фібоначчі задається таким чином: F1 = F2 = 1, Fk = Fk−1 + Fk−2, K>= 3.
Це твердження можна довести методом математичної індукції, попередньо впорядкувавши числа L1, L2, ..., Lk за неспаданням. Оскільки F45 > 109 (у чому можна переконатися, написавши спеціальну «дослідницьку» програму), серед будь-яких 45 натуральних чисел, які не перевищують 109, обов’язково знайдуться три, що є сторонами трикутника. Отже, зокрема і серед 45 найдешевших відрізків знайдуться три, що утворюють трикутник. Але ціни відрізків — перестановка чисел від 1 до N, тому сумарна ціна цих трьох відрізків не може перевищувати 45 + 44 + 43 = 132. Таким чином, усі відрізки вартістю більше за 132 можна відкинути й шукати потрібну трійку лише серед тих, що залишилися. Маємо фактично лінійне від N розв’язання з додатком, що складає порядку 1323 операцій.
|
Варіант 1
|
Варіант 2
|
|
#include "fstream"
using namespace std;
long int l[1000000],c[1000000],s,n,i,j,k;
ifstream cin("segments.dat");
ofstream cout("segments.sol");
int main()
{cin>>n;
for(i=0;i<n;i++)cin>>l[i]>>c[i];
s=2000000000;
for(i=0;i<n-2;i++)
for(j=i+1;j<n-1;j++)
for(k=j+1;k<n;k++)
if (l[i]<l[j]+l[k] && l[j]<l[i]+l[k] && l[k]<l[j]+l[i] && c[i]+c[j]+c[k]<s)
s=c[i]+c[j]+c[k];
if (s<2000000000)cout<<s<<endl;else cout<<-1<<endl;
return 0;
}
|
#include "fstream"
using namespace std;
long int a[1000000],ans,n,i,j,u,l,c,k;
ifstream cin("segments.dat");
ofstream cout("segments.sol");
int main()
{cin>>n;
k=3000;
for(i=0;i<n;i++){cin>>l>>c;
a[c]=l;}
ans=2000000000;
for (i = 1; i <= n; i++)
for (j = i + 1; j <= n; j++)
for (u = j + 1; u <= n; u++)
if (i + j + u < ans && a[i] < a[j] + a[u] && a[j] < a[i] + a[u] & a[u] < a[i] + a[j]) ans = i + j + u;
if (ans==2000000000)ans=-1;
cout<<ans<<endl;
return 0;
}
|
|
|
Последнее обновление 06.10.14 11:38 |
|