|
Добавил(а) Administrator
|
|
14.09.16 00:00 |
|
Заннятя 2 (14.09.2016)
1. Базові структури.
Розв’язати і протестувати задачі в системі (http://134.249.159.199/cgi-bin/new-client?contest_id=23)
Логін school2016-1 . . . school2016-10 (пароль - 1)
2. Повідомляємо, що на сайті http://netoi.org.ua (http://www.olymp.vinnica.ua) почаласяреєстраціяучасниківвідкритоїВсеукраїнськоїІнтернет-олімпіадизінформатики NetOI-2016
http://www.olymp.vinnica.ua/index_ua.php?lng=ua&cid=1679
Ви можете самі взяти в ній участь і порекомендувати це зробити тим, кого, на вашу думку, це може зацікавити.Якщо Ви школяр, обов'язково повідомте про олімпіаду своїм учителям інформатики.
Задача DEMO_A
На площині задано координати двох відрізків AB і CD. Знайти спільну частину проекцій цих відрізків на вісь абсцис.
Вхідні дані
Ви вводите з клавіатури 8 цілих чисел - координати точок A, B, C, D. Кожне число не перевищує за абсолютною величиною 1000.
Вихідні дані
Ви виводите на екран одне число - спільну частину проекцій. Якщо спільна частина - порожня множина, вивести -1, якщо це одна точка - вивести 0.
Приклад вхідних та вихідних даних
Вхід: 2 2 7 5 3 4 8 1
Вихід: 4
Задача DEMO_B
Скільки натуральних чисел виду 2a3b5ca,b,c - невід'ємні цілі числа) належать відрізку [M;N]?
Вхідні дані
Ви вводите з клавіатури 2 цілих числа M та N. Кожне з чисел не перевищує за абсолютною величиною 10000.
Вихідні дані
Ви виводите на екран одне число - шукану кількість чисел.
Приклад вхідних та вихідних даних
Вхід: 10 20
Вихід: 6
Задача DEMO_C
Дана послідовність N цілих чисел. Знайти найменший додатній елемент цієї послідовності.
Вхідні дані
Ви вводите з клавіатури кількість чисел N та N цілих чисел - елементів цієї послідовності. Число N не перевищує 10000, кожний елемент послідовності не перевищує за абсолютною величиною 1000.
Вихідні дані
Ви виводите на екран одне число - шуканий елемент послідовності. Якщо у послідовності немає додатніх елементів - вивести 0.
Приклад вхідних та вихідних даних
Вхід: 7 -4 4 -7 3 0 8 2
Вихід: 2
Задача DEMO_D
Задано натуральне число N. Знайти найменше та найбільше число, яке складається з тих самих цифр та у такій самій кількості, що і N.
Вхідні дані
Ви вводите з клавіатури число N (1£ N £2000000000).
Вихідні дані
Ви виводите в одному рядку найменше число, а через пропуск - найбільше число.
Приклад вхідних та вихідних даних
Вхід: 7051
Вихід: 1057 7510
Задача DEMO_E
Задано текстовий рядок. Вилучити з нього всі символи, що не є цифрами. Вважається, що рядок містить хоча б одну цифру.
Вхідні дані
Ви вводите з клавіатури заданий рядок, довжина якого не перевищує 255 символів.
Вихідні дані
Ви виводите на екран шуканий рядок.
Приклад вхідних та вихідних даних
Вхід: Ф11р88н
Вихід: 1188
Задача DEMO_F
Дано K клітин шахової дошки. З'ясувати, чи всі вони одного кольору.
Вхідні дані
Ви вводите з клавіатури кількість контрольних прикладів, потім число К - кількість клітин шахової дошки,а у наступних К рядках - координати клітин (натуральні числа, не більші 8).
Вихідні дані
Ви виводите на екран для кожного приклада 1, якщо всі клітини одного кольору і 0, якщо це не так.
Приклад вхідних та вихідних даних
|
Вхід:
|
3
|
| |
|
3
|
|
|
1
|
2
|
|
8
|
1
|
|
8
|
5
|
|
2
|
|
|
1
|
1
|
|
1
|
2
|
|
2
|
|
|
1
|
1
|
|
2
|
2
|
|
Вихід: 101
Увага! Це не заліковий тур!
Парне+парне, непарне-непарне –чорна
Парне+непарне, непарне-парне –біла
$13. Дистанційне навчання *(http://dystosvita.mdl2.com/ )
Програмування в С++
Основи програмування (Python)
|
|
Добавил(а) Administrator
|
|
07.09.16 00:00 |
|
Заннятя 1 (07.09.2016)
Завдання 1 (http://kpi-open.org/tasks/ )
Недобросовісний МЕНЕДЖЕР
Менеджер транспортної компанії таємно співпрацює з постачальником палива і зацікавлений в максимальному його витраті. Як йому скласти маршрутну карту відвідування вантажівкою N міст, розташованих уздовж однієї траси на однаковій відстані одне від одної, таким чином, щоб витрата палива був найбільшим?
Формат вхідного файлу
Вхідний файл складається з одного рядка, що містить три цілих числа, відокремлених один від одного пробілом: N - кількість міст (10 <= N <= 25000), D - відстань між містами, F - витрата палива на одиницю шляху.
Формат вихідного файлу
Вихідний файл складається з одного рядка, що містить ціле число, рівне витраті палива.
|
Введення
|
Виведення
|
|
12 1 5
|
|
|
125 5 10
|
|
|
325 5 1
|
|
Завдання 2
https://www.e-olymp.com/uk/problems/2669
Поворот
Задано масивn×m. Потрібно повернути його за годинниковою стрілкою на90градусів.
Вхідні дані
У першому рядку задано натуральні числаnтаm(1≤n,m≤50). У наступнихnрядках записано поmневід'ємних чисел, які не перевищують109- сам масив.
Вихідні дані
Виведіть перевернутий масив у форматі вхідних даних.
Ліміт часу1секунда
Ліміт використання пам'яті64MiB
Вхідні дані #1
3 4
1 2 3 4
5 6 7 8
9 10 11 12
Вихідні дані #1
4 3
9 5 1
10 6 2
11 7 3
12 8 4
Завдання 3
https://www.e-olymp.com/uk/problems/1378
Фібоначчієва система числення
Як відомо, послідовність Фібоначчі починається з двох чисел 0 та 1 і кожен наступний член послідовності отримується як сума двох попередніх. Наприклад, третій член послідовності це 1 (1=1+0), четвертий - 2 (2=1+1), п'ятий - 3 (3=2+1) і т.д.
|
i
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Fib(i)
|
0
|
1
|
1
|
2
|
3
|
5
|
8
|
13
|
21
|
34
|
Рисунок 1 - Перші числа послідовності Фібоначчі
Ця послідовність проявляється дуже часто і у нашому житті і у природі та має велике значення. А чи знаєте Ви, що всі додатні цілі числа можна подати як суму чисел з послідовності Фібоначчі? Більше того, всі натуральні числа можна подати за допомогою послідовності Фібоначчі, причому без повторень. Наприклад: 13 може бути подано за допомогою вказаної множини як {13}, {5,8} або {2,3,8} а 17 подано як {1,3,13} або {1,3,5,8}. Так як всі числа мають цю властивість (може у Вас є бажання довести це?), то цей набір є гарним способом для його використання у якості "бази" (основи системи числення) для подання чисел. Але, як ми бачили вище, деякі числа можуть бути подані більш ніж одним способом сумою чисел з послідовності Фібоначчі. Як нам вийти з цієї ситуації? Дуже просто! Для цього достатньо накласти обмеження, що при поданні числа не можна використовувати два сусідніх елементи з послідовності Фібоначчі! Це обмеження поясюється тим, що сума двох сусідніх членів послідовності Фібоначчі сама є членом послідовності Фібоначчі.
Тепер, коли нам відомо все сказане вище, ми можемо запропонувати гарний спосіб подавння довільного цілого додатнього числа. Для цього ми будемо використовувати двійкову послідовність (лише нулів та одиниць). Наприклад, 17 = 1 + 3 + 13 (ми повинні пам'ятати, що не можна використовувати два послідовних числа Фібоначчі). Будемо використовувати нуль у запису, якщо чергове число з послідовностіи Фібоначчі не використовується, і одиницю для тих, що використовуються. Тоді, 17 = 100101 (ведучі нулі повинні бути відсутні). На рисунку 2детально показано, як отримано цей запис і що означають нулі та одиниці у наведенному вище запису. Для кращого розуміння цієї схеми звернемо увагу на той факт, що не використання двох сусідніх чисел Фібоначчі означає, що двійкова послідовність не буде мати двох одиниць, що йдуть підряд. Використовуючи наведене подання числа, ми будемо говорити, що ми використовуємо Фібоначчієву систему числення і записувати його як 17 = 100101 (fib).
|
17=
|
1
|
0
|
0
|
1
|
0
|
1
|
|
13+3+1=
|
13
|
8
|
5
|
3
|
2
|
1
|
Рисунок 2 - Пояснення подання числа 17 у Фібоначчієвій системі числення
Ваша задача полягає у запису задного десяткового числаув Фібоначчієвій системі числення.
Вхідні дані
У першому рядку вхідних даних задано єдине натуральне число N, яке вказує на кількість прикладів у тесті (1 ≤ N ≤ 500).
Наступні N рядків містять по одному додатньому цілому числу, яке не перевищує 100 000 000. Числа можуть бути подані у довільному порядку.
Вихідні дані
Ви повинні вивести по одному рядку для кожного з N чисел, отриманих у вхідних даних, у наступному форматі: "DEC_BASE = FIB_BASE (fib)". DEC_BASE це задане оригінальне число у десятковій системі числення, а FIB_BASE відповідно - його подання у Фібоначчієвій системі числення. Зразок виведення наведено у прикладі вихідних даних.
Ліміт часу 1 секунда
Ліміт використання пам'яті 64 MiB
Вхідні дані
10
1
2
3
4
5
6
7
8
9
10
Вихідні дані
1 = 1 (fib)
2 = 10 (fib)
3 = 100 (fib)
4 = 101 (fib)
5 = 1000 (fib)
6 = 1001 (fib)
7 = 1010 (fib)
8 = 10000 (fib)
9 = 10001 (fib)
10 = 10010 (fib) |
|
|
Пошук у ширину та глибину, ейлерів та гамільтонів графи |
 |
 |
 |
|
Добавил(а) Administrator
|
|
16.02.11 14:25 |
|
Задача 1. (Властивості Ейлера) Є N поселень. Деякі поселення попарно з'єднані стежками. За ними ніякі дві стежки загальних точок не мають. В цілочисельній таблиці СТЕЖКИ [1..N,1..N] задана інформація про стежки; кількість стежок між і-m і j-m рівна значенню елемента таблиці СТЕЖКИ [і,j]=СТЕЖКИ[j,і]>0 (в тому числі і=j); Написати алгоритм, який визначає, чи можливо зобразити карту стежок, не відриваючи олівця від паперу і не малюючи жодної стежки двічі.
Задача 2. (Пошук в глибину)
Турбаза мала для ночівлі N місць, з’єднаних стежками. Туристів можна вести в одну сторону. Довжина стежки – одноденний перехід. Пройти і перевірити всі M-денні маршрути, які починаються на базі K.
Вас найняли для того, щоб визначити мiсця дипломатiв за столом обговорень мiжнародної конференцiї. На конференцiю запрошенi по одному дипломату з N рiзних країн свiту. Кожен дипломат знає вiд однiєї до М мов. Дипломати, якi не знають спiльної мови, не можуть розмовляти один з одним. До того ж, деякi країни проголосили, що не будуть пiдтримувати дипломатичних стосункiв з деякими iншими, тобто представники цих країн не будуть розмовляти один з одним. Ваше завдання полягає в розробцi програми DIPLOMAT.*, що визначає мiсця за столом для дипломатiв таким чином, щоб кожен мiг розмовляти з обома своїми сусiдами, якi сидять лiворуч та праворуч вiд нього.
Стiл, що використовується, круглий i розрахований на N персон. Дипломат може спiлкуватись з дипломатом, який сидить лiворуч однiєю мовою, а з дипломатом, що сидить праворуч, – iншою.
Вхiднi данi:
В першому рядку текстового файлу DIPLOMAT.DAT – число N. Далi – N рядкiв, по одному рядку на дипломата. Кожен рядок – послiдовнiсть слiв. Сусiднi слова вiдокремленi пропуском. Кожне слово – це послiдовнiсть великих латинських лiтер. Перше слово – код країни – складається з 3 лiтер. Друге слово має довжину вiд 1 до 5 лiтер i представляє перелiк мов, на яких може спiлкуватись дипломат. Кожна мова позначена однiєю лiтерою. Далi iде список з не бiльш як N трилiтерних слiв – кодiв країн, з якими уряд дипломата пiдтримує стосунки.
Вихiднi данi:
До файлу DIPLOMAT.SOL треба вивести список дипломатiв в порядку розмiщення за столом (по одному дипломату в рядку). Кожен рядок складається з 3 слiв: перше – код мови, якою дипломат може спiлкуватись з сусiдом лiворуч, друге – код країни дипломата, третє – код мови для спiлкування з сусiдом праворуч. Можливе iснування декiлькох розв'язкiв. Вам потрiбно знайти один. Якщо розв'язку не iснує, Ваша програма повинна видати таке повiдомлення: NO SOLUTION EXISTS.
|
Приклад вхiдних даних
|
Приклад вихiдних даних
|
|
10
USA EF CHN GBR USR FRA FRG JPN ISR POR KOR
CHN CFE USA GBR FRA FRG
GBR ER USA CHN USR FRA FRG JPN ISR POR KOR
USR RF USA GBR FRA FRG
FRA F USA CHN GBR USR FRG JPN ISR POR
FRG ERG USA CHN GBR USR FRA JPN ISR POR
JPN JHG USA GBR FRA FRG JPN ISR POR KOR
ISR YER USA GBR FRA FRG JPN KOR
POR PGE USA GBR FRA FRG JPN
KOR KEC USA GBR USR JPN ISR
|
E USA E
E KOR E
E ISR H
H JPN G
G FRG G
G POR E
E GBR E
E USR F
F FRA F
F CHN E
|
procedure p(ni,v:integer);
var s,ii:integer;
begin
c[ni]:=v;
if(ni=n)then begin
{***** 1}
for ii:=1 to ni do write(c[ii]);
end
else
for ii:=1 to n do
if (a[v,ii]>0)and (f(ni,ii)) then p(ni+1,ii);
end;
Практична робота «Пошук у ширину та глибину, ейлерів та гамільтонів графи»
|
№
|
Завдання
|
Результат
|
|
1.
|
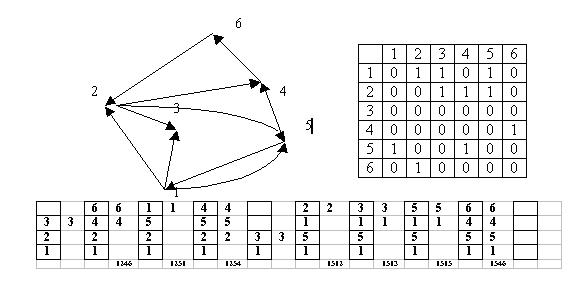
Намалювати граф з кількістю вершин N=6
(ненавантажений, неорієнтований)
|
|
|
2.
|
Написати матрицю суміжності
|
|
|
3.
|
Скопіювати папку «!Лабораторна 9 графи» в свою папку
Занести матрицю в файл graph.dat
|
|
|
4.
|
За допомогою програми graph1.dpr відшукати всі шлях з вершини 1 довжиною 3 (шлях з 4 вершин)
|
|
|
5.
|
За допомою програми graph2.dpr відшукати всі гамільтонові шляхи
|
|
|
6.
|
За допомою програми graph3.dpr відшукати ейлеровий шлях
|
|
|
7.
|
За допомогою програми graph4.dpr створити навантажений неорієнтований граф та відшукати найкоротший гамільтонів шлях
|
|
N
|
|
|
3
|
|
|
5
|
|
|
7
|
|
|
9
|
|
|
10
|
|
|
12
|
|
|
13
|
|
|
20
|
|
|
50
|
|
|
100
|
|
|
|
8.
|
Зробіть висновок
|
|
|
|
Побудова опуклої оболонки |
 |
 |
 |
|
Добавил(а) Гісь І.В.
|
|
25.11.10 16:58 |
|
|
|
Последнее обновление 25.11.10 17:40 |
|