Интерполяция

Вычисление коэффициентов интерполирующей рациональной функции
Интерполируемая функция представляется, как отношение двух полиномов.

Интерполяция полиномом Лагранжа
Полиномиальная интерполяция.

Интерполяция по Ньютону
Полиномиальная интерполяция. Немного другой алгоритм, тот же результат.

Интерполяция кубическими сплайнами
Неплохой способ интерполяции, быстрый и устойчивый к погрешностям.

Коэффициенты тригонометрического полинома

Билинейное ресэмплирование (билинейная интерполяция)
Функция задана на сетке M₁ xN₁ , осуществляется переход к сетке M₂ xN₂ .

Построение кривой Безье
Построение кривой Безье

Введение

Цель этого введения - рассказать о преимуществах и недостатках различных методов интерполяции. Вообще, задачи интерполяции можно поделить на два класса: одномерная и многомерная интерполяция. Здесь, в основном, приведены методы одномерной интерполяции.

Из всех способов одномерной интерполяции можно выделить три основных - полиномиальная, рациональная и сплайн-интерполяция. При полиномиальной интерполяции функция представляется в виде полинома степени N-1, где N - число точек с известными значениями интерполируемой функции. При рациональной интерполяции функция представляется в виде отношения двух полиномов. При сплайн-интерполяции используется кусочно-кубическое представление функции. У каждого способа есть свои преимущества и недостатки.

Рациональная интерполяция является очень точной, но, к сожалению, обладает существенным недостатком - полученное представление функции далеко не всегда является непрерывным и может иметь полюса в тех точках, где оригинальная функции полюсов не имеет.

У полиномиальной интерполяции есть другая слабость - существуют функции, которые очень плохо интерполируются полиномами. На рисунке ниже приведен результат полиномиальной интерполяции по 11 точкам функции f(x) = (ArcTan(1+x ²)) ^-1.

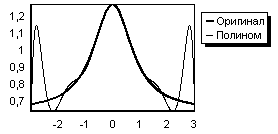
Жирной линией показана сама функция, тонкой линией - результат интерполяции. Как видно, около границ интервала погрешность интерполяции очень резко возрастает, несмотря на то, что интерполируемая функция проходит через все указанные ей точки. С увеличением числа точек погрешность не уменьшается, а наоборот возрастает. Такое поведение свойственно функциям, которые имеют полюса на комплексной плоскости в круге, на котором проводится интерполяция. Так, указанная функция имеет полюса в точках x₁  = i, x₂  = -i.

Сплайн-интерполяция лишена такого недостатка (в данном случае результат интерполяции просто сливается с графиком оригинала) и в случае большого числа точек является даже более быстрой, чем полиномиальная или рациональная интерполяция.

Если нашли ошибку в алгоритме - сообщите!

Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU