Интерполяция полиномом Лагранжа по Эйтекену

Пусть задано n+1 значение функции F_i  = F(x_i ) в разных точках: x₀ , x₁ , ..., x_n . Тогда полином степени не выше n, имеющий в заданных узлах значение F_i , есть полином Лагранжа:

Вычисление значений L_n (x) по данной формуле осуществляется по итерационной формуле Эйтекена. Интервалы [x_i , x_i+1 ] могут быть неравными.

Если точки x₀ , .., x_n  заданы извне, то больше говорить не о чем. Если же у нас есть свобода выбора точек, в которых мы будем брать значение функции, то можно повысить точность интерполяции на определенном отрезке [a, b] за счет особого способа выбора точек. Если выбирать точки так, что они будут находиться в корнях полинома Чебышева n+1-ой степени, определенного на отрезке [a, b], то достигается минимальная возможная погрешность для данного числа точек на данном отрезке. Это расположение определяется следующими формулами:

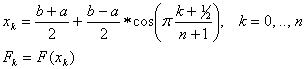
Такое расположение, помимо всего прочего, делает вычислительный процесс устойчивым при больших n. Обычно с ростом числа точек начинают накапливаться вычислительные погрешности, но при указанном расположении погрешности нейтрализуют друг друга.

Если нашли ошибку в алгоритме - сообщите!

Реализации алгоритма на различных языках:

Блоксхемы:

Реализация алгоритма на AlgoPascal:

unit LagrangeInterpolateUnit;

interface
    LagrangeInterpolate;
implementation
(*
Полином Лагранжа по Эйтекену.

function LagrangeInterpolate(n:integer;x,F:array [0..n] of real;y:real):real;

интерполирует функцию, принимающую в точках x[i] значение F[i].
Функция возвращает значение полинома в точке t.
*)
function LagrangeInterpolate(
    const   n   :   Integer;
    const   x   :   array of Real;
            F   :   array of Real;
            t   :   Real):Real;
var
    I   :   Integer;
    J   :   Integer;
begin
    for j:=0 to n-1 do
    begin
        for i:=j+1 to n do
        begin
            F[i]:=((t-x[j])*F[i]-(t-x[i])*F[j])/(x[i]-x[j]);
        end;
    end;
    Result:=F[n];
end;

end.

Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU