Вычисление коэффициентов интерполирующей рациональной функции

Если задано m значений функции F_i  = F(x_i ) в m точках x₁ , x₂ , ..., x_m , то F(x) может быть определено по формуле:

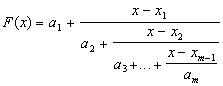
Эта непрерывная дробь может быть представлена в виде рациональной функции:

где l не превосходит m₁  = trunc(m/2).

Вообще-то, рациональные функции - очень точный способ интерполяции, намного точнее полиномов или сплайнов... в тех случаях, когда этот способ работает. При некоторых входных данных не удается построить интерполирующую функцию данным способом и алгоритм прекращает работу с ошибкой деления на ноль. Не то чтобы по данному набору точек вообще нельзя было построить рациональную функцию, просто данным способом это не получится. Поэтому данный способ интерполяции хорош, если есть возможность заранее проверить и убедиться в его работоспособности.

Если нашли ошибку в алгоритме - сообщите!

Реализации алгоритма на различных языках:

Блоксхемы:

Реализация алгоритма на AlgoPascal:

unit ContinuousFractionsUnit;

interface ContinuousFractionsInterpolate;

implementation
(*
Процедура строит интерполирующую рациональную функцию по заданным точкам.
На входе:
    m   -   число точек
    x,y -   массивы аргументов и значений в заданных точках с номерами
            элементов от 0 до m.

На выходе:
    m1  -   степень числителя и знаменателя интерполирующей функции.
    b   -   коэффициенты числителя
    d   -   коэффициенты знаменателя
Коэффициенты числителя и знаменателя имеют номера от 0 до m1, где i-ый
коэффициент стоит при X в степени I.
*)

procedure ContinuousFractionsInterpolate(
            m   :   Integer;
    const   xa  :   array of Real;
    const   ya  :   array of Real;
    out     m1  :   Integer;
    out     b   :   array of Real;
    out     d   :   array of Real);
var
    I   :   Integer;
    J   :   Integer;
    K   :   Integer;
    
    R   :   Real;
    S   :   Real;
    A   :   array of Real;
    P   :   array of Real;
    Q   :   array of Real;
begin
    m:=m+1;
    m1:=m div 2;
    SetBounds(b, [0, m1]);
    SetBounds(d, [0, m1]);
    SetBounds(a, [1, m]);
    SetBounds(p, [0, m]);
    SetBounds(q, [0, m]);

    for j:=1 to m do
    begin
        r:=ya[j-1];
        s:=xa[j-1];
        if j<>1 then
            for i:=1 to j-1 do
                r:=(s-xa[i-1])/(r-a[i]);
        a[j]:=r;
    end;

    p[0]:=1;
    q[0]:=a[1];
    k:=1;
    repeat
        for i:=1 to m1 do
        begin
            p[i]:=0;
            q[i]:=0;
        end;

        for i:=2 to m do
        begin
            for j:=i div 2 downto 1 do
            begin
                r:=a[i]*q[j]-xa[i-2]*p[j]+p[j-1];
                p[j]:=q[j];
                q[j]:=r;
            end;
            r:=a[i]*q[0]-xa[i-2]*p[0];
            p[0]:=q[0];
            q[0]:=r;
        end;
        
        if k=2 then
        begin
            k:=1;
            for i:=0 to m1 do
                d[i]:=q[i];
        end
        else
        begin
            k:=2;
            for i:=0 to m1 do
                b[i]:=q[i];
            p[0]:=0;
            q[0]:=1
        end;
    until not(k=2);
end;


end.

Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU