Поиск корней уравнения четвертой степени вида: x ⁴+ax ³+bx ²+cx+d = 0

Процедура находит все корни уравнения четвертой степени. Известно, что возможно три варианта: четыре действительных корня, два действительных корня и два комплексно сопряженных или четыре комплексных попарно сопряженных корня. В первом случае корни уравнения помещаются в массив x, во втором случае на выходе из процедуры в переменных x[1] и x[2] содержатся действительные корни, а в переменных x[3] и x[4] соответственно действительная и мнимая части комплексно сопряженных корней, в третьем случае в переменных x[1] и x[2] содержиться соответственно действительная и мнимая части одной пары комплексно сопряженных корней, а в переменных x[3] и x[4] - другой. Количество действительных корней находиться в переменной nr.

При решении уравнения используется метод Феррари, вначале находится действительный корень y₁  кубического уравнения:

при этом в случае когда три действительных корня берется максимальный. Для решения кубического уравнения используется предыдущий алгоритм. Затем корни исходного уравнения находяться как корни двух квадратных уравнений:

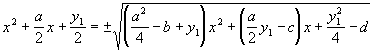
при этом следует отметить, что подкоренное выражение в правой части является полным квадратом.

Если нашли ошибку в алгоритме - сообщите!

Блоксхемы:

К сожалению, для данного алгоритма нет исходного кода. Это не ошибка и сообщать мне об этом не надо. Возможно, для алгоритма ещё не успели создать исходный код, или же при переносе алгоритма из старой версии библиотеки возникли проблемы с исходником и его написание пришлось отложить до лучших времен. Попробуйте воспользоваться прилагаемыми файлами и блок-схемой или поискать на сайте аналогичный алгоритм, но с исходником.

Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU