Поиск корней кубического уравнения вида: x ³+ax ²+bx+c = 0

Процедура находит все корни кубического уравнения. Известно, что возможно два варианта: три действительных корня, либо один действительный корень и два комплексно сопряженных. В первом случае корни уравнения помещаются в массив x, во втором случае на выходе из процедуры в переменной x[1] содержится действительный корень, а в переменных x[2] и x[3] соответственно действительная и мнимая части комплексно сопряженных корней. Количество действительных корней содержится в переменной nr.

Для решения уравнения вначале делаем подстановку x = y-a/3 в результате которой исходное уравнение преобразуется к виду: y ³+py+q = 0, где p = -a ²/3+b, q = 2(a/3) ³-ab/3+c. Далее вычисляем: Q = (p/3) ³+(q/2) ².

если Q - отрицательно (откуда очевидно p - отрицательно), уравнение имеет три действительных корня, которые получаются по формулам:

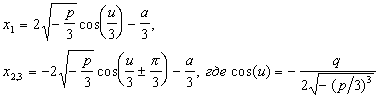
если Q = 0 - уравнение имеет три действительных корня, которые получаются по формулам:

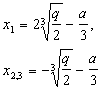
если Q - положительно, то корни уравнения получаются по формулам:

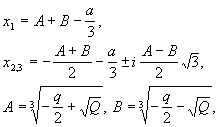
Если нашли ошибку в алгоритме - сообщите!

Реализации алгоритма на различных языках:

Блоксхемы:

Реализация алгоритма на AlgoPascal:

unit CubicEquationUnit;

interface
    SolveCubicEquation;
implementation

(******************************************************
процедура решает кубическое уравнение x^3+ax^2+bx+c=0

procedure SolveCubicEquation(
    a,b,c:real;
    var nr:byte;
    x:array[1..3] of real);

Процедура находит все корни кубического уравнения.
Известно, что возможно два варианта: три действительных
корня, либо один действительный корень и два комплексно
сопряженных. В первом случае корни уравнения помещаются
в массив x, во втором случае на выходе из процедуры в
переменной x[1] содержится действительный корень, а в
переменных x[2] и x[3] соответственно действительная и
мнимая части комплексно сопряженных корней. Количество
действительных корней содержится в переменной nr.

При расчётах приходится сравнивать результат вычислений
с нолем. В таком случае сравнивается модуль числа и
epsilon.
******************************************************)
procedure SolveCubicEquation(
    const   a   :   Real;
    const   b   :   Real;
    const   c   :   Real;
    out     nr  :   Integer;
    out     x   :   array of Real;
    const   Epsilon : Real);
var
    AH  :   Real;
    BH  :   Real;
    p   :   Real;
    q   :   Real;
    QH  :   Real;
    u   :   Real;
begin
    SetBounds(x, [1,3]);
    
    p:=-a*a/3+b;
    q:=2*a/3*a/3*a/3-a*b/3+c;
    QH:=(p/3)*(p/3)*(p/3)+(q/2)*(q/2);
    if AbsReal(QH)<Epsilon then
    begin
        nr:=3;
        AH:=AbsReal(q/2);
        if AbsReal(AH)>Epsilon then
        begin
            AH:=sign (q)*exp(ln(AH)/3)
        end;
        x[1]:=2*AH-a/3;
        x[2]:=-AH-a/3;
        x[3]:=-AH-a/3
    end
    else
    begin
        if QH>0 then
        begin
            AH:=-q/2+sqrt(QH);
            AH:=sign (AH)*exp(ln(AbsReal(AH))/3);
            BH:=-q/2-sqrt(QH);
            BH:=sign (BH)*exp(ln(AbsReal(BH))/3);
            x[1]:=AH+BH-a/3;
            if AbsReal(AH-BH)<Epsilon then
            begin
                nr:=3;
                x[2]:=-(AH+BH)/2-a/3;
                x[3]:=-(AH+BH)/2-a/3
            end
            else
            begin
                nr:=1;
                x[2]:=-(AH+BH)/2-a/3;
                x[3]:=(AH-BH)/2*sqrt(3)
            end;
        end
        else
        begin
            nr:=3;
            u:=-q/2/sqrt(-p*p*p/27);
            u:=arccos(u);
            x[1]:=2*sqrt(AbsReal(p/3))*cos(u/3)-a/3;
            x[2]:=-2*sqrt(AbsReal(p/3))*cos(u/3+Pi()/3)-a/3;
            x[3]:=-2*sqrt(AbsReal(p/3))*cos(u/3-Pi()/3)-a/3
        end;
    end;
end;



end.

Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU