Рекурсия
Цель сегодняшнего занятия познакомится с
рекурсией, реккурентностями и алгоритмами их
реализации.
К концу занятия Вы опираясь на полученные
знания сможете самостоятельно изобразить
алгоритм выполнения рекурсии.
Рекурсия - это одна из фундаментальных
концепций в математике и программировании,
Рекурсия - это одна из форм мышления, это мощное
средство, позволяющее строить элегантные и
выразительные алгоритмы.
Объект называется рекурсивным, если он
содержит сам себя или определен с помощью самого
себя.
Если процедура р содержит явное обращение к
самой себе, то она называется явно рекурсивной.
Если процедура р содержит обращение к
некоторой процедуре q, которая в свою очередь
содержит прямое или косвенное обращение к р, то р
- называется косвенно рекурсивной.
Но рекурсивная программа не может вызывать
себя бесконечно, иначе она никогда не
остановится, таким образом в программе (функции)
должна присутствовать еще один важный элемент -
так называемое терминальное условие, то есть
условие при котором программа прекращает
рекурсивный процесс.
Рекуррентности.
Реккурентность - это рекурсивное определение
функции. Они широко распространены в математике.
Возможно наиболее знакомая Вам из такого рода
функций - это факториал. Факториал - это
произведение натуральных чисел от единицы до
какого - либо данного натурального числа. Он
определяется формулой:
N!=N((N-1)!, для N>=1 и 0! = 1.
Это напрямую соответствует нижеследующей
рекурсивной программе:
function factorial( N : integer ) : integer;
begin
if N=0 then
factorial := 1
else
factorial := N * factorial(N-1);
end;
Эта программа демонстрирует основные свойства
рекурсивных программ: программа вызывает сама
себя (с меньшим значением аргумента), и у нее есть
терминальное условие при котором она прямо
вычисляет результат.
Необходимо также помнить о том, что это -
программа, а не формула: например ни формула, ни
программа не работают с отрицательными N, но
губительные последствия попытки произвести
вычисления для отрицательного числа более
заметны для программы, чем для формулы. Вызов
factorial(-1) приведет к бесконечному рекурсивному
циклу. Поэтому перед вызовом данной программы
нужно делать проверку условия
неотрицательности.
Второе, хорошо известное рекуррентное
соотношение - соотношение определяющее числа
Фибоначчи. Числа Фибоначчи - это элементы
числовой последовательности 1,1, 2, 3, 5, 8 ..., в
которых каждый последующий элемент равен сумме
предыдущих.
FN = FN-1 + FN-2, где N >= 2 и F0 =
F1 = 1.
И снова, рекуррентность соответствует простой
рекурсивной программе:
function fibonacci( N : integer ) : integer;
begin
if N<=1 then
fibonacci := 1
else
fibonacci := fibonacci( N-1 ) + fibonacci( N-2
);
end;
Как мы увидим, многие интересные алгоритмы
можно легко реализовать с помощью рекурсивных
программ, и многие разработчики алгоритмов
предпочитают выражать алгоритмы рекурсивно. Но
часто случается также и так, что столь же
интересный алгоритм скрывается в деталях
нерекурсивной реализации. Давайте рассмотрим
такой алгоритм.
const
max = 25;
var
i : integer;
F : array [0..max] of integer;
procedure fibonacci;
begin
F[0] := 1;
F[1] := 1;
for i := 2 to max do
F[i] := F[i-1]+F[i-2];
end;
Эта программа вычисляет первые max чисел
Фибоначчи, используя массив размера max. Этот
метод называет итерационным.
Какой же метод лучше? Точных правил для выбора
между рекурсивной и нерекурсивной версиями
алгоритма решения задачи не существует.
Краткость и выразительность большинства
рекурсивных процедур упрощает их чтение и
сопровождение. С другой стороны, выполнение
рекурсивных процедур требует больших затрат и
памяти, и времени процессора нежели их
итерационные аналоги.
Деление пополам.
Большая часть алгоритмов использует два
рекурсивных вызова, каждый из которых работает
примерно с половиной входных данных. В дизайне
алгоритмов такое явление называют "деление
пополам"; его часто используют для достижения
существенной экономии.
В качестве примера, давайте рассмотрим задачу
нанесения делений на линейку: на ней должна быть
метка в точке 1/2", метка немного покороче через
каждые 1/4", еще более короткая через 1/8" и так.
Линейка
Мы также предполагаем, что в наше распоряжение
предоставлена процедура mark( x, h) для нанесения
метки высоты h единиц на линейку в позицию x.
Центральная метка должна иметь высоту n единиц,
метки в центрах левой и правой половинок - n-1
единиц, и так далее. Следующая рекурсивная
программа - прямой путь достижения нашей цели:
procedure rule( l, r, h : integer );
var m : integer;
begin
if h>0 then
begin
m := (l+r) div 2;
mark( m, h );
rule( l, m, h-1);
rule( m, r, h-1);
end;
end;
Идея этого метода заключается в следующем: для
того, чтобы промаркировать линейку, мы сперва
наносим длинную метку по ее середине. Это делит
ее на две равные половины. Теперь мы наносим
(более короткие) метки в середине каждой из этих
половинок используя ту же самую процедуру.
Необходимо обращать особое внимание на
терминальное условие рекурсивной программы - в
противном случае она никогда не остановится! В
вышеприведенной программе мы терминируем, когда
мы должны нанести метку высоты 0. Рассмотрим
пример, в результате вызова rule(0, 8, 3). Мы ставим
метку по середине и вызываем rule для левой
половины, затем делаем тоже самое для левой
половины, и так далее пока высота метки не станет
равна 0. В конечном итоге мы возвращаемся из rule и
размечаем правую половину подобным образом.
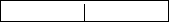 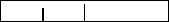
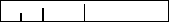
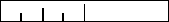
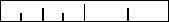
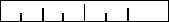
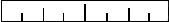
|
rule(0,8,3)
mark(4,3)
rule(0,4,2)
mark(2,2)
rule(0,2,1)
mark(1,1)
rule(0,1,0)
rule(1,2,0)
rule(2,4,1)
mark(3,1)
rule(2,3,0)
rule(3,4,0)
rule(4,8,2)
mark(6,2)
rule(4,6,1)
mark(5,1)
rule(4,5,0)
rule(5,6,0)
rule(6,8,1)
mark(7,1)
rule(6,7,0) |
Дерево рекурсивных вызовов для
рисования линейки.
Другой нерекурсивный алгоритм заключается в
том, чтобы рисовать сперва самые короткие метки,
затем чуть менее короткие и так далее, как
показано в следующей, довольно компактной,
нерекурсивной программе:
procedure draw(l, r, h : integer);
var
i, j : integer;
begin
j:=1;
for i:=1 to h do
begin
for x:=0 to (l+r) div j do
mark(l+j+x*(j+j),i);
j:=j+j;
end;
end;
Нерекурсивное рисование
линейки
Сейчас создадим двухмерный узор
демонстрирующий то, как простая рекурсия может
дать решение тому, что кажется сложным.
Фрактальная звезда (слева) и ее
очертания(справа)
uses
graph,crt;
var
r,gd,gm: Integer;
procedure star(x,y,r:integer);
begin
if r>2 then begin
star(x+r,y+r,r div 2);
star(x+r,y-r,r div 2);
star(x-r,y-r,r div 2);
star(x-r,y+r,r div 2);
bar(x-r,y-r,x+r,y+r);
end;
end;
begin
clrscr;
Gd := Detect;
write('Enter the lenght: ');
readln(r);
InitGraph(Gd, Gm, 'с:\bp\bgi');
if GraphResult <> grOk then
Halt(1);
setbkcolor(0);
SetFillStyle(1, 9);
star(getmaxx div 2,getmaxy div 2,r);
repeat
until keypressed;
end.
Рисующий примитив здесь - просто процедура
которая рисует квадрат размера 2r с центром в (x, y).
Рекурсивно определенные геометрические узоры
подобные этому называют фракталами. Если
используется более сложный примитив для
рисования и более сложные рекурсивные вызовы
(особенно на вещественной и комплексной
плоскостях), то можно разработать узоры
поразительной красоты и сложности.
Итак, на сегодняшнем занятии мы
познакомились с рекуррентостями и рекурсией. |