Понятие комбинаторной задачи
Сначала мы приведём довольно общие рассуждения, которые имеют отношение
к решению произвольных нетривиальных (или как их называют в узком смысле –
``олимпиадных'') задач, а потом переходим к непосредственному разбору
конкретных комбинаторных задач, используя введённые понятия.
1.1 Процесс решения задачи
Существенным отличием задач, рассматриваемых при изучении информатики и
математики, является то, что они ``полностью определены'', т.е. четко
описаны на подходящем языке. Чаще всего это язык математики.
Задачи, с которыми мы сталкиваемся в реальной жизни, не являются
полностью определёнными. Чаще всего они описаны на естественном языке,
который с точки зрения формального описания обладает четырьмя недостатками:
он неполон, избыточен, неодназначен и неточен.
Поставить задачу означает прежде всего понять условие задачи
(т.е. удалить неполноту, избыточность и неодназначность) или, другими
словами, найти соответствующее представление. На самом деле задача понята
только тогда, когда найдено такое представление, в котором все элементы
задачи представлены без избыточности и многозначности.
Условие задачи при этом записываются в
формализованном виде. Задача становится одновременно и более абстрактной
и более строгой. В этом случае говорят о задаче в замкнутой форме или о
замкнутой формулировке задачи.
С математической точки зрения можно предложить такой общий шаблон для
задачи в замкнутой форме:
Найти в заданном множестве X элементы x, удовлетворяющие заданным
ограничениям K(x).
Примером такой задачи может служить задача решения уравнения:
``из множества натуральных чисел x выбрать такие числа, которые
удовлетворяют уравнению x3+84=37x''.
Для одной и той же задачи всегда можно привести несколько разных
замкнутых формулировок. Не всегда при этом есть одна наиболее ``естественная''
формулировка. (Слово ``естественная'' в данном случае надо понимать не как
``напрашивающаяся'', а скорее как ``наиболее простая''.) Если даже такая
формулировка одна, не всегда просто её найти. Иногда нахождение такой
формулировки – основное в решении задачи.
Подход человека к решению задачи включает следующие основные этапы:
- Выяснение смысла условий задачи.
- Первые выводы из условий задачи.
- Проигрывание ситуации, обдумывание.
- Выбор наилучшего представления – поиск замкнутой формулировки задачи.
- Частичное (возврат к пункту 2) или общее решение.
- Проверка и обобщение решения.
1.2 Понятие комбинаторной задачи
Понятие комбинаторной задачи не имеет строгого определения.
Иногда говорят о комбинаторных задачах в достаточно узком смысле слова,
имея в виду практические задачи, при решении которых возникают проблемы с
большим (и часто неприемлемым) количеством операций (а, значит, и времени).
Мы будем иметь дело с учебными задачами и нам ближе следующий подход.
Задачу имеет смысл называть комбинаторной, если ее решение состоит в
переборе элементов x множества X. (При этом наравне с термином
``комбинаторная'' вполне подходит термин ``переборная''.)
Как видим, такое определение описывает не саму задачу, а скорее
её решение. Ведь, подходя формально, любую задачу можно пытаться решать
таким методом. Надо заметить, что никакого парадокса здесь нет. Действительно,
очень большое количество реальных задач – задачи переборные и только
для некоторых найдены способы избегать перебора.
1.3 Пространство перебора
Итак, предположим, мы решаем задачу с помощью перебора. При этом
решение будет состоять в переборе элементов множества X и проверке
условий K(x) для каждого такого элемента.
Множество X в данном случае называется пространством перебора.
Для полного
решения задачи необходимо выполнить по крайней мере |X|·|K| шагов
(не считая шагов, необходимых для порождения элементов множества X),
где |X| – количество элементов множества X, а |K| – количество
шагов, необходимых для проверки одного элемента.
Понятно, что размер множества X очень важен для эффективного решения задачи.
Часто множество X является декартовым произведением множеств
X1,...,Xn (т.е. состоит из наборов элементов (x1,...,xn), где
xi О Xi).
При этом сократив множество перебора для каждого Xi в два раза,
мы сократим общий объём перебора в 2n раз.
Таким образом, очень важно
получить замкнутую формулировку
с небольшим пространством перебора. И совершенно
неприемлемы формулировки с бесконечным пространством перебора. Иногда,
переходя от формулировки к формулировке и сокращая перебор, удаётся
полностью его избежать и решить задачу ``прямым'' методом.
1.4 Как избежать перебора
При решении нестандартных задач невозможно дать конкретный рецепт
для того, как сократить перебор или вообще его избежать. Единственное, что
можно определенно сказать – это то, что сократить перебор – значит,
по-существу, получить новую замкнутую формулировку задачи.
Рассмотрим лучше конкретный пример. На нём мы проследим этапы
решения задачи.
Задача 1. Пусть имеется шахматная доска, каждая сторона которой содержит 100 клеток.
Все 10000 полей доски заняты чёрными шашками. Разрешёнными ходами являются
операции замены в каком-то ряду (строке или столбце)
всех шашек чёрного цвета на белые и белых на чёрные. Спрашивается, можно
ли за конечное число ходов получить 1990 белых шашек?
Первой, непосредственной замкнутой формулировкой может быть поиск
последовательности ходов. Каждый ход задаётся
указанием того, со строкой или столбцом производится замена цвета и
номером строки или столбца. Но такая формулировка совершенно непригодна
для проведения перебора, так как пространство перебора бесконечно.
Если проиграть ситуацию (возможно мысленно) на модели доски (например,
размером 4 ґ 4), появляются следующие заключения:
- Если дважды подряд заменяют цвет у одного и того же ряда, позиция
не меняется.
- Пусть мы хотим сделать два хода (a и b). От того, какой ход мы
сделаем первым, а какой – вторым, результат не зависит.
Это определяется тем,
что разные строки, как и столбцы, не имеют между собой общих шашек. У
пересекающихся строки и столбца – только одна общая шашка, которая при
любом порядке ходов в результате вернется к исходному цвету.
- На основании двух первых заключений можно сделать вывод, что
порядок ходов не является существенным и, кроме того,
результирующее состояние ряда
то же при 2n+k ходах, что и при k ходах. Таким образом, пространство
перебора сокращается:
надо перебирать всевозможные
множества строк и столбцов с которыми будет проведена замена цвета. Таких
множеств уже конечное число, хотя всё же ещё очень много - 220000.
- После того, как сделан ход, номер ряда не является существенным,
так как в задаче важным является лишь число шашек белого цвета, но не место
их расположения.
- На основании предыдущего вывода можно строки, у которых был
изменён цвет один раз, перенести в верхнюю часть доски, а столбцы
соответственно – в левую часть. Таким образом доска окажется разбитой на
четыре части:
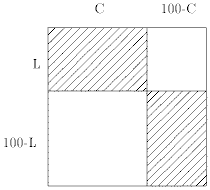
Число строк L в верхних и число столбцов C в левых прямоугольниках
соответствуют рядам шашек, модифицированных один раз.
Таким образом, пространство перебора ещё более сокращается:
надо перебирать всевозможные пары (L,C). Объем пространства перебора уже
вполне приемлемый – 10000.
- Представленная на доске позиция обладает симметрией относительно
строк и столбцов. Если (L,C) – решение задачи, то и (C,L) также будет
решением.
- Рассматриваемая позиция обладает ещё и центральной симметрией.
Если (L,C) – решение задачи, то и (100-C,100-L) также будет
решением.
Теперь пространство перебора можно задать как пары (L,C), в которых
LЈ C, L Ј 100-C и его объём – 2100.
Однако на этом мы не остановимся, а продолжим изучение задачи. Запишем
замкнутую формулировку. Число белых шашек составляет:
вверху — Lґ (100-C) и внизу — Cґ (100-L). В результате
условие, которой должна удовлетворять искомая пара можно записать в виде:
100(L+C)-2LC=1990
Становится очевидным, что достаточно перебирать только первый элемент пары
— L, а C вычислять по формуле
C=(1990-100L)/(100-2L)
и проверять на приемлемость. Таким образом, пространство перебора сокращается
до 50 элементов.
На данном этапе задачу целесообразно немного обобщить.
Мы сведём эту задачу к решению простого
уравнения в целых числах.
Пусть p – половина длины доски
и n – число, равное половине заданного числа белых шашек.
Тогда можно записать
p(L+C)-LC=n
Сделаем замену переменных L=l+p, C=c+p. Получим уравнение
lc=p2-n
Целое число, стоящее справа, известно. Это 50ґ 50 - 1990/2=1505.
Для существования решения необходимо, чтобы число 1505 было разложимо
на множители, сопоставимые с размерами доски.
1505=5ґ 7ґ 43, а так как p=50, то -50Ј l Ј 50,
-50Ј c Ј 50. В данном случае имеется решение, удовлетворяющие
этим условиям: l=5ґ 7, c=43, L=85, C=93
(или симметричное ему l=-5ґ 7, c=-43, L=15, C=7).
Таким образом, имеется вариант получения на доске 1990 белых шашек.
Следующая часть,
Содержание
