Рассмотрим задачу о расстановке n ферзей.
Задача 2 N ферзей. На шахматной доске размером nґ n требуется расставить n ферзей, так, чтобы они не били друг друга.
Построим замкнутую формулировку этой задачи. Позицию будем записывать в виде набора, состоящего из координат x, y всех ферзей. Условие xi № xj (yi № yj) означает то, что i-ый и j-ый ферзи стоят на разных вертикалях (горизонталях). Условия xi+yi № xj+yj и xi-yi № xj-yj означают что i-ый и j-ый ферзи не стоят на одной диагонали. Получаем следующую замкнутую формулировку: Найти набор (x1,y1,x2,y2,...,xn,yn), xi, yi О {1,...,n}, такой что: xi № xj, yi № yj, xi+yi № xj+yj, xi-yi № xj-yj для всех i, j О {1,...,n}. Заметим, что среди координат x ферзей x1,x2,...,xn ровно один раз встречается каждое из чисел 1,2,...,n. Таким образом, достаточно перебирать только координаты y. Номера же ферзей можно рассматривать как координаты x. Итак, переформулируем задачу: Найти набор (y1,y2,...,yn), yi О {1,...,n}, такой что: yi № yj, i+yi № j+yj, i-yi № j-yj для всех i, j О {1,...,n}.
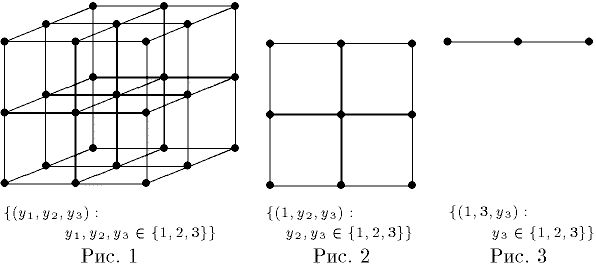
Нарисуем пространство для n=3 (это слишком небольшое число для данной задачи и в этом случае вообще нет решения, но нам важно понять, что представляет из себя пространство перебора). Пространство перебора – множество {(y1,y2,y3) : y1,y2,y3 О {1,2,3}}. На рисунке элементы пространства перебора отмечены точками.

Напрашивающийся алгоритм перебора состоит в последовательном переборе сначала (т.е. на верхнем уровне перебора) трёх плоскостей, потом – прямой на плоскости (см. рисунок 2) и наконец – точки на прямой. Каждый уровень перебора соответствует перебору положения для одного ферзя.
В общем случае такой алгоритм состоит в последовательном переборе сначала положения для первого ферзя, после каждого выбора такого положения – в переборе положения для второго ферзя и т.д. Алгоритм записывается с помощью n вложенных циклов:
for i1 := 1 to n do begin
ферзь[1] := i1;
for i2 := 1 to n do begin
ферзь[2] := i2;
for i3 := 1 to n do begin
ферзь[3] := i3;
...
... <проверка построенной позиции>
end;
end;
end;
Приведённый алгоритм типичен. Пространство перебора часто состоит из наборов элементов и те значения, которые может принимать каждый элемент, перебираются последовательно – после выбора значения для одного элемента перебираются все возможные значения для следующего и т.д.
Таким образом, пространство перебора всегда – параллелепипед. (В общем случае – множество наборов {(y1,...,yn) : y1 О Y1, yn О Yn}, Y1, ..., Yn Н Y.) Такое пространство можно задать, задав множества Y1, ..., Yn. В нашем случае это означает, что мы должны указать, какие значения разрешены для каждого из ферзей. Так мы приходим к компактному представлению пространства перебора, с которым и будем работать в дальнейшем.
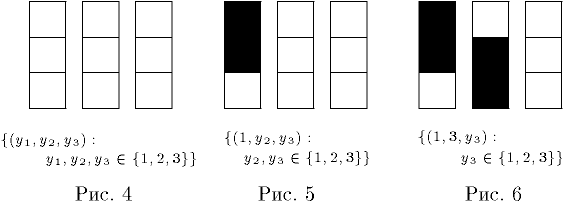
На рисунках 4, 5, 6 показаны те же пространства перебора, что и на рисунках 1, 2, 3 соответственно. Там, где значение для ферзя запрещено – квадрат изображён чёрным цветом, где разрешено – белым. В дальнейшем мы будем вертикали, соответствующие ферзям изображать вплотную (у нас получится шахматная доска).
Проследим, какими будут первые полностью построенные позиции при приведённом алгоритме. Сначала будет рассмотрен вариант, когда все ферзи занимают положение 1, потом последний ферзь займёт положение 2 и т.д. Но постойте! Ведь уже когда первый ферзь занимает положение 1, то все позиции, в которых второй ферзь занимает положение 1 или 2 будут заведомо неприемлемы. Т.о. первые 2 · nn-2 вариантов будут рассмотрены впустую. Но ведь это можно было заметить уже при расстановке второго ферзя.
Иначе говоря, из пространства перебора заведомо можно удалить варианты, когда второй ферзь занимает положение 1 или 2. Для случая n=3 сокращённое пространство перебора показано на рис. 3.
Такое сокращение можно реализовать проверкой совместимости положения выбираемого ферзя с выбранными ранее. Улучшенный алгоритм будет выглядеть следующим образом. (Мы специально не приводим конкретный алгоритм, который будет немного более эффективным, а записываем алгоритм в общей форме, которая подойдёт и для решения других задач).
for i1 := 1 to n do begin
ферзь[1] := i1;
for i2 := 1 to n do begin
ферзь[2] := i2;
{ проверка частично построенной позиции }
if <ферзь[2] не бьёт ферзь[1]> then
for i3 := 1 to n do begin
ферзь[3] := i3;
{ проверка частично построенной позиции }
if <ферзь[3] не бьёт предыдущих> then
for i4 := 1 to n do begin
...
if <ферзь[n] не бьёт предыдущих> then
<решение найдено>
end;
end;
end;
end;
Понятно, что очень важно отсечь ненужные варианты на наиболее ранних этапах перебора. При этом мы по-существу отсекаем сразу группу ``лишних'' вариантов.
При сокращении пространства перебора надо иметь в виду насколько сокращается пространство и соотносить размер этого сокращения с затратами на его реализацию. Если размер сокращения не велик по сравнению с общим объёмом перебора, то обычно не стоит ``городить огород'' и реализовывать такое сокращение, так как затраты на выполнение более сложной схемы перебора могут ``съесть'' весь выигрыш от сокращения. Кроме того, каждое усложнение алгоритма – лишняя возможность сделать ошибку.
Приём использования симметрии дал возможность в задаче о шашках несколько раз переформулировать задачу и предельно сократить пространство перебора. Действительно, сначала мы использовали симметрию различных последовательностей одних и тех же ходов, потом симметрию различных строк (столбцов) доски, потом центральную симметрию и поворот на 90°.
Симметрию часто удаётся использовать и в процессе перебора (а не только при переформулировке задачи). Так например, в задаче о ферзях за счёт симметрии можно считать, что первый ферзь находится на нижней половине доски. Это сократит перебор в два раза. Очень сильно сокращается перебор за счёт симметрии в рассматриваемой в следующем разделе задаче о раскраске карты.
Часто при проверке перебираемых вариантов многие операции повторяются для разных элементов пространства перебора. Напрашивается следующая идея оптимизации: выполнять эти операции сразу для групп элементов. Причём чем больше группы, тем лучше. По-существу, сокращение пространства перебора в последнем рассмотренном варианте задачи о ферзях осуществляется как раз за счёт отсечения сразу группы элементов. Кроме того, позиция тоже строится не для каждого варианта с самого начала, а насколько это возможно сразу для групп вариантов. Это делают операторы ферзь[1] := i1; ... , которые виднуты на максимально верхний уровень.
В результате группирования алгоритм может существенно измениться.
Выразительные примеры (5 и 6) приведены в следующем
разделе.
Следующая часть,
Содержание