Задача g6_1068: Террористы (Украинские учебно-тренировочные сборы 2001. Оригинальное название "Игра")

В стране есть несколько аэропортов, и рейсы между ними. Можно долететь с одного аэропорта до другого, возможно с пересадками, но для любой пары аэропортов существует единственный маршрут перелета.
Два террориста играют в такую игру. Они делают ходы по очереди. Каждый ход состоит из таких операций. Игрок минирует аэропорт, выбирает рейс и улетает вместе с коллегой. После взлета он активирует взрывное устройство, в результате чего аэропорт взрывается и все рейсы до и из этого аэропорта отменяются. После приземления в другом аэропорту ход переходит к другому игроку. Проигрывает тот, кто не может сделать ход.
Задача
Напишите программу GAME которая по начальному списку рейсов и номеру аэропорта где в начале игры находятся террористы определит кто победит, если каждый игрок будет придерживаться оптимальной стратегии.
Входные данные
Первая строка входного текстового файла GAME.DAT содержит два целых: N - количество аэропортов (N <= 1000) и K - номер исходного аэропорта. Следующие N -1 строк содержат пары целых чисел - номера аэропортов, соединенных рейсом (все рейсы - двухсторонние и упоминаются только раз). В каждом аэропорту не более 20 рейсов.
Выходные данные
Единственная строка выходного текстового файла GAME.SOL должна содержать 0, если первый игрок проигрывает, или номер аэропорта, в который необходимо полететь, если первый игрок выигрывает. Если есть несколько "выигрышных" аэропортов, необходимо найти аэропорт с минимальным номером.
Пример входных данных
4 3
3 2
3 1
1 4
Пример выходных данных
2

Решение g6_1068:
Веселая задача! Во-первых, прочитаем первое условие: "для любой пары аэропортов существует единственный маршрут". Ясно, что структура данных, используемая в этой задаче - дерево. Его можно хранить, как динамический список сыновей, например, для каждой вершины указывая на левого сына и правого брата. Но структура данных - не самое главное в этой задаче, а самое главное - сама суть решения.
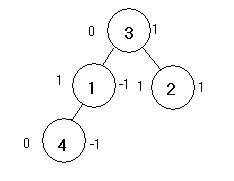
Теперь я приведу свой рисунок дерева для входных данных (ну не умею я рисовать!), а потом объясню, что означают цифры слева и справа от кружков:

Итак, перейдем к значению левой цифры: она означает четность вершины, т.е. расстояние от корня дерева, до этой вершины. Это понадобиться нам в некоторых случаях для определения того, какой игрок выиграл. Если вершина не имеет сыновей (т.е. лететь больше некуда), и ее четность равна 0 (ход первого игрока), то первый игрок, летя таким маршрутом, проигрывает; если же четность равна 1 и у вершины нет сыновей, то проигрывает второй игрок. Кстати, какой игрок выигрывает или проигрывает показывает цифра справа от кружка - если выигрывает первый игрок, то эта цифра равна 1, если проигрывает -1.
Теперь будем определять, выиграет или нет игрок в вершине, у которой есть сыновья. Если вершина имеет 0 четность (ход первого игрока), то, естественно, он должен выбрать среди сыновей такой маршрут, который обеспечивает ему выигрыш - т.е. если среди его сыновей есть сын с числом 1 справа, то первый игрок может выбрать выигрышный маршрут и этой вершине также присваивается значение 1. Если же четность вершины равна 1 (ходит второй игрок), то он должен стараться выбрать наихудший вариант для первого игрока, т.е. если у вершины есть сын с выигрышем -1, то и этой вершине присваивается -1.
Технически это реализуется с помощью рекурсивной процедуры и динамического массива. Если значения потомков не определены, то для них запускается рекурсивная процедура, если вершина не имеет потомков, то в динамический массив записывается выигрыш исходя из определенного нами правила. Если же значения всех потомков определены, то среди них выбирается наибольший или наименьший, соответственно четности вершины, и этот результат также записывается в массив.
Здесь было бы уместно применить альфа-бета отсечение, т.е. если при 0 четности мы нашли сына с выигрышем 1, то можно не искать других сыновей, однако нам надо найти наименьший номер аэропорта, в который надо полететь, а альфа-бета отсечение может "отсечь" этот вариант, так что придется обходиться без него.
Кстати, поиск номера выигрышного аэропорта надо осуществлять так: идем по всем аэропортам, начиная с наименьшего, и, если этот аэропорт имеет выигрыш 1 и не имеет сыновей, проверяем, все ли его предки имеют выигрыш 1 (для этого в списке надо хранить также указатель на предка). Если все предки имеют выигрыш 1, то выводим номер этого аэропорта. Поиск такого аэропорта можно организовать и по-другому.
Скачать тесты к задаче