Линейное уравнение Вольтерра второго рода

Линейное интегральное уравнение Вольтера второго рода имеет вид:

Причем независимые переменные x, s изменяются на промежутке [a, b], ядро k(x, s) непрерывно внутри и на сторонах треугольника, ограниченного прямыми s = a, x = b, x = s. Функция f(x) на [a, b] непрерывна.

Уравнение данного типа решается с помощью метода квадратурных формул, суть которого состоит в замене интегрального уравнения апроксимирующей системой алгебраических уравнений относительно дискретных значений искомой функции и решении этой системы. В основе такой замены лежит приблежение интеграла квадратурными формулами. Применение формулы трапеций с постоянным шагом h приводит к рекурентной формуле:

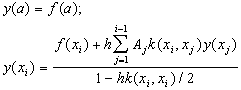
где

• i = 2, 3, ..., 1+(b-a)/h
• x_i  = a+(i-1)/h
• A_j  = 1 при j > 1 и A_j  = 0.5 при j = 1.

Если нашли ошибку в алгоритме - сообщите!

Реализации алгоритма на различных языках:

Блоксхемы:

Реализация алгоритма на AlgoPascal:

unit Volterra2Unit;

declaration
    function F(X : Real):Real;
    function K(X : Real; S : Real):Real;

interface SolveVolterra2;

implementation


(******************************************************************
Процедура  решает  интегральное  уравнение  Вольтерра второго рода,
заданное   ядром   интегрирования   K(X,S) и правой частью F(X), на
отрезке [A, B].

Результат помещается в массив Y с номерами элементов от 1 до N, где
1 соответствует A, N соответсвует B.
******************************************************************)
procedure SolveVolterra2(
    const A : Real;
    const B : Real;
    const N : Integer;
    out   Y : array of Real);
var
    G   :   Real;
    H   :   Real;
    K1  :   Real;
    X   :   Real;
    
    I   :   Integer;
    J   :   Integer;
    
begin
    SetBounds(y, [1, N]);
    
    h:=(b-a)/(n-1);
    y[1]:=F(a);
    for i:=2 to n do
    begin
        x:=a+(i-1)*h;
        g:=F(x);
        for j:=1 to i-1 do
        begin
            k1:=K(x,a+(j-1)*h);
            if j=1 then
            begin
                k1:=k1/2;
            end;
            g:=g+h*k1*y[j];
        end;
        y[i]:=g/(1-h*K(x,x)/2);
    end;
end;


end.

Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU