АЛГОРИТМЫ

Новости

Рассылка новостей

Форум

AlgoPascal

Редактор блок-схем

Статьи

О сайте

Контакты

Алгоритмы растровой графики (Часть вторая)

Автор: Быстрицкий В.Д. При написании, использовались материалы статьи С.Л. Островского Алгоритм Брезенхема построения окружности

В предыдущей статье, посвященной растровой графике, мы рассмотрели алгоритмы построения отрезка, а так же закраски области экрана. Теперь рассмотрим еще один часто используемый алгоритм, а именно алгоритм Брезенхема построения окружности.

Но вначале оговорим условия нашей работы (для тех кто не читал первой части). Будем считать, что устройством, на которое происходит вывод графики, является массив Screen: array [0.. ScW-1,0..ScH-1] of TColor. Здесь TСolor означает, что элементы массива задают цвет соответствующей точки устройства. Для задания цвета мы будем использовать функцию RGB(bR,bG,bB:byte), параметры которой задают соотношения красного, зеленого и синего цвета, т.е. например такая запись Screen[12,15]:=RGB(255,255,255) будет означать, что мы "закрашиваем" точку с координатами (12,15) белым цветом. Будем так же полагать, что точке с координатами (0,0) соответствует левый верхний угол устройства вывода при этом увеличение первой координаты, означает движение точки по горизонтали, а второй по вертикали (хотя в данной статье направление осей не имеет особого значения).

Из геометрии мы знаем, что окружность с центром в точке (xc,yc) и радиусом r, задается параметрически с помощью системы уравнений:

м

x = xс+r cosa

 y = yс+r sina

    где a О [0;2p).
н
о
Отсюда не сложно получить алгоритм генерации окружности:

  1. Полагаем А=0.
  2. Если А больше либо равно 2p, то окружность отрисована.
  3. Вычислим x=Trunc(xc+r*cos(A)), y=Trunc(yc+r*sin(A))
  4. Screen[x,y]=Color
  5. Увеличим A на d (A:=A+d) и перейдем к шагу 2.

В данном алгоритме d подбираем в зависимости от радиуса окружности и разрешающей способности устройства вывода. При малых значениях d возможно неоднократная активация одних и тех же точек, при больших - возможны "пробелы" в сгенерированной окружности. Но основная причина по которой использование данного алгоритма нецелесообразно, не сложность в выборе параметра d, а очень низкая скорость работы, связанная с использованием вещественных чисел, и тем более вычислением тригонометрических функций.

Но не будем спешить отказываться от этого алгоритма. Его простота поможет нам получить некоторые усовершенствования, которые можно будет использовать в дальнейшем.

Для начала постараемся уменьшить количество вычислений, воспользуемся свойством симметрии окружности относительно диаметра, будем расчитывать только координаты точек верхней полуокружности, а нижнию половину получать используя свойство симметрии. Новый алгоритм будет иметь вид:

  1. Полагаем А=0.
  2. Если А больше либо равно p, то окружность отрисована.
  3. Вычислим x=Trunc(r*cos(A)), y=Trunc(r*sin(A))
  4. Screen[xc+x,yc+y]=Color
  5. Screen[xc+x,yc-y]=Color
  6. Увеличим A на d (A:=A+d) и перейдем к шагу 2.

Чуть побыстрее, но не настолько чтобы успокоиться. Однако выделим две простые идеи, используемые в этом алгоритме, которые будут нам полезны в дальнейшем. Первая заключается в том, что на шаге 3 мы вычисляем координаты (x,y) точки на окружности радиуса r с центром в начале координат, а на шаге 4 просто осуществляем сдвиг. Второе, благодаря симметрии, мы имеем: если точка (x,y) лежит на окружности с центром в точке (0,0), то и точка (x,-y), так же лежит на этой окружности. Последнее утверждение можно развить, а именно: если точка (x,y) лежит на окружности с центром в точке (0,0), то и точки (x,-y);(-x,-y);(-x,y);(y,x),(y,-x);(-y,-x);(-y,x), так же лежат на этой окружности. Для проверки можно использовать следуюшие уравнение задающие окружность: 

	x2+y2=r2

Итак вся подготовительная работа выполнена. Теперь немного пофантазируем, допустим у нас есть функция(назовем ее NextPoint(x,y,r)) которая выдает нам точки лежащие на окружности с центром в нуле и радиуса r, при этом пусть это будут точки из красного сектора (см. рисунок):

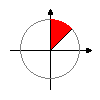
тогда наш алгоритм можно будет записать в виде

  1. y:=r; x:=0;
  2. Screen[x+xc,y+yc]:=Color;
  3. Screen[x+xc,-y+yc]:=Color;
  4. Screen[-x+xc,y+yc]:=Color;
  5. Screen[-x+xc,-y+yc]:=Color;
  6. Screen[y+xc,x+yc]:=Color;
  7. Screen[y+xc,-x+yc]:=Color;
  8. Screen[-y+xc,x+yc]:=Color;
  9. Screen[-y+xc,-x+yc]:=Color;
  10. NextPoint(x,y,r);
  11. Если получили новую точку то на шаг 2, иначе окружность нарисована.

Дело за малым придумать как работает функция NextPoint. Вот здесь и начинается самое интересное. Нетрудно заметить, что координата x в красном секторе увеличивается на единицу на каждом шаге (для проверки можно, например, подсчитать производную функции y=f(x), задающей кусок окружности - она будет больше 1). Так же ясно, что координата y либо уменьшается на единицу, либо остается без изменений. Итак нам осталось научиться выбирать куда переходить из точки (xi,yi) либо в точку (xi+1,yi), либо в точку (xi+1,yi-1). Для того, чтобы оcуществить выбор рассмотрим две невязки: 

	di1=(xi+1)2+yi2-r2
	di2=(xi+1)2+(yi-1)2-r2
А так же будем следить за их суммой: 
	di=di1+di2

Рассмотрим несколько вариантов расположения "вещественной" окружности относительно "целых" точек:



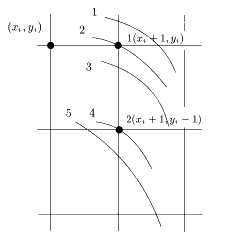
Интуитивно понятно, что в случаях 1 и 2 надо "зажигать" точку 1, а в случаях 4 и 5 - точку 2, случай 3 требует более тщательного рассмотрения. Попробуем формализовать все пять случаев при помощи введенных параметров di; di1; di2: Случай 1. di1 < 0, di2 < 0, и следовательно di < 0.
Случай 2. di1= 0, di2 < 0, и следовательно di < 0.
Случай 3. di1 > 0, di2 < 0, и следовательно имеем два варианта для di:
   Случай 3.1. |di1| < |di2| и следовательно di < 0.
   Случай 3.2. |di1| > |di2| и следовательно di > 0.
Случай 4. di1 > 0, di2=0, и следовательно di > 0:
Случай 5. di1 > 0, di2 > 0, и следовательно di > 0:

Подводя итог имеем: в случае, если di < 0 надо активировать точку (xi+1,yi), а в случае, если di > 0 надо активировать точку (xi+1,yi-1). Осталось получить выражение для di 

	di=di1+di2=(xi+1)2+yi2-r2+(xi+1)2+(yi-1)2-r2=2xi2+2yi2+4xi-2yi+3-2r2

Теперь получим выражение di+1 через di, избавившись от неприятной операции возведения в квадрат. Пусть вначале yi+1=yi, тогда 

	di+1=2xi+12+2yi+12+4xi+1-2yi+1+3-2r2=di+4xi+6

Теперь пусть yi+1=yi-1, тогда 

	di+1=2xi+12+2yi+12+4xi+1-2yi+1+3-2r2=di+4(xi-yi)+10

Осталось получить занчение d1 в начальной точке (x1=0,y1=r): 

	d1=3-2r

Уф-ф-ф! Все! Теперь можно записать полученный алгоритм:

  1. y:=r; x:=0; d:=3-2r
  2. Если x > y, то выходим.
  3. Screen[x+xc,y+yc]:=Color;
  4. Screen[x+xc,-y+yc]:=Color;
  5. Screen[-x+xc,y+yc]:=Color;
  6. Screen[-x+xc,-y+yc]:=Color;
  7. Screen[y+xc,x+yc]:=Color;
  8. Screen[y+xc,-x+yc]:=Color;
  9. Screen[-y+xc,x+yc]:=Color;
  10. Screen[-y+xc,-x+yc]:=Color;
  11. Если d < 0, то d:=d+4*x+6, переходим на Шаг 13
  12. d:=d+4(x-y)+10; y:=y-1;
  13. x:=x+1
  14. Переходим на Шаг 2.

Сравниваем с нашим первым алгоритмом - практически ничего похожего, первый был понятен, но работал медленно, во втором сходу угадать, что он рисует окружность невозможно, но зато скорость работы потрясающая.

Также можно посмотреть блок-схему и исходник алгоритма.


 


Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU