
АЛГОРИТМЫ
Новости
Рассылка новостей
Форум
AlgoPascal
Редактор блок-схем
Статьи
О сайте
Контакты
Алгоритмы растровой графики (часть первая).
Автор: Быстрицкий В.Д.
- Введение
- Алгоритмы генерации растрового представления отрезка
- Алгоритм закраски многоугольников
- Алгоритм закраски произвольной области с затравкой
Введение
В данной статье я попытаюсь описать простейшие алгоритмы растровой графики, такие как генерация отрезка прямой, окружности или эллипса, алгоритма закраски многоугольника или, в более общем случае, области плоскости.
Практически любой современный язык программирования имеет стандартные процедуры, которые решают эти задачи (не говоря о том, что для Windows набор таких алгоритмов является просто «системными» функциями). В связи с этим возникает вопрос для чего вообще необходимо изучать эти алгоритмы? Но в любом деле следует начинать с чего-то и если Вы собираетесь в дальнейшем решать задачи связанные с графикой, то знать, как реализуются простейшие из алгоритмов просто необходимо.
Мы будем изучать алгоритмы в общем виде, поэтому определимся с некоторыми условиями нашей работы. Будем считать, что устройством, на которое происходит вывод графики, является массив Screen: array [0.. ScW-1,0..ScH-1] of TColor. Здесь TСolor означает, что элементы массива задают цвет соответствующей точки устройства. Для задания цвета мы будем использовать функцию RGB(bR,bG,bB:byte), параметры которой задают соотношения красного, зеленого и синего цвета, т.е. например такая запись Screen[12,15]:=RGB(255,255,255) будет означать, что мы "закрашиваем" точку с координатами (12,15) белым цветом. Будем считать, что если нам необходимо, мы можем не только присваивать значение элементу массива, но и считывать цвет точки с произвольными координатами. В случае некоторого "реального" устройства будем считать, что точке с координатами (0,0) соответствует левый верхний угол при этом увеличение первой координаты, означает движение точки по горизонтали, а второй по вертикали.
Прежде чем перейти непосредственно к алгоритмам генерации растровых изображений, определим еще несколько понятий, которые в дальнейшем будут нам полезны.
Назовем точки 4-соседями (или "непосредственными" соседями), если у них отличается только одна из координат и притом только на 1. Назовем точки 8-соседями (или "косвенными" соседями), если у них отличается горизонтальная или вертикальная координата, но не более чем на 1. Не трудно заметить, что всякий непосредственный сосед является также и косвенным соседом. Всякая точка имеет 4 непосредственных и 8 косвенных соседей.
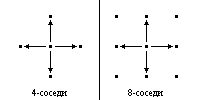
Итак, вводная часть закончена и мы можем перейти к рассмотрению алгоритмов, начнем мы естественно главного без чего нельзя обйтись при работе с графикой, а именно построения отрезка заданного своими концами.
Алгоритмы генерации растрового представления отрезка
Для начала выскажем общие соображения относительно построения отрезка на экране.
Допустим, нам даны координаты начала (x1 , y1 ) и конца (x2 , y2 ) отрезка, тогда уравнение прямой, содержащей отрезок, может быть, записано в виде y = y1 +k(x-x1 ), где k = (y2 -y1 )/(x2 -x1 ), а x пробегает значения от x1 до x2 (мы пока исключаем из рассмотрения случай вертикального отрезка). Поскольку растровое изображение отрезка содержит только точки с целочисленными координатами, то x будет пробегать только целые значения из отрезка (x1 , x2 ). И в случае |k| < 1 все прекрасно: изменяем значение x, по уравнению прямой, высчитываем значение y, "закрашиваем" точку с координатами (x, y), переходим к началу цикла. Но не трудно заметить, что в случае когда |k| > 1, наше представление отрезка будет иметь пробелы, так как изменение x на единицу приведет к изменению y более чем на единицу. Поэтому в случае |k| > 1 переменные x и y надо поменять ролями.
Итак, мы практически получили искомый алгоритм, но вот только x и y могут, а в общем случае и будут, принимать вещественные значения, что для нас совершенно не допустимо, таким образом, нам надо ввести некоторое соглашение о том каким образом мы будем "округлять" вещественные значения к целым. В связи с вопросом округления вернемся к определению 4-х и 8-ми связности.
Я представлю два алгоритма Брезенхема получения 4-х и 8-ми связного представления отрезка, заданного координатами концов. Разницу между двумя этими представлениями можно увидеть на рисунке:
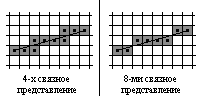
И тот и другой алгоритм используют только целочисленную арифметику, что естественно улучшает скорость работы. Саму структуру алгоритмов можно понять из блок-схем, которые приведены на странице графики (4-х связное представление, 8-ми связное представление). Различие в работе понятно и связано с разницей между 4-х и 8-ми связным представлением: в случае 4-х связности на каждом шаге мы изменяем на единицу только одну из координат текущей точки, а в случае 8-ми связности мы можем менять сразу и вертикальную и горизонтальную координаты текущей точки, но снова не более чем на единицу.
Алгоритм закраски многоугольников
Под многоугольником далее будем понимать фигуру, ограниченную на плоскости простой (непересекающейся) замкнутой ломаной. Сама ломаная задается координатами вершин Ai (xi , yi ), i = 1, ..., n, при этом соседние точки в этом списке являются вершинами ломаной. Задача "закраски" многоугольника заключается в инициализации все его внутренние точки.
Наиболее простой, но и наиболее медленный алгоритм, решающий эту задачу состоит в том, чтобы проверить все точки плоскости (под плоскостью здесь естественно понимается устройство, на которое осуществляется вывод, в нашем случае это массив Screen) на принадлежность многоугольнику. Несколько ускорить этот алгоритм можно, если вместо проверки всех точек плоскости проверять только точки минимального квадрата заключающего многоугольник, найти который, не составляет труда. Ясно, что и при таком усовершенствовании скорость работы алгоритма оставляет желать лучшего. Для проверки принадлежности точки многоугольнику можно использовать алгоритм, который приведен на странице геометрии.
Еще один вариант решения задачи, это алгоритм сканирования строк. Последовательно проходим все горизонтальные линии плоскости, и находим отрезки на прямой, внутренние для многоугольника. Для данного алгоритма достаточно искать только точки пересечения сканирующей линии с ребрами многоугольника. Для оптимизации алгоритма можно упорядочить ребра в порядке возрастания наибольшей из ординат концов. При перемещении сканирующей прямой сверху вниз проверке на пересечение подвергаются лишь те ребра, у которых значение максимальной ординаты больше ординаты сканирующей прямой.
Такой алгоритм пригоден для заполнения произвольных многоугольников. Но если многоугольник выпуклый, то алгоритм можно упростить и существенно повысить его эффективность. Для этого заметим, что границу выпуклого многоугольника можно разбить на две ломаные "левую" и "правую" и, возможно, два ребра "верхнее" и "нижнее" так что каждая из боковых ломаных имеет ровно одно пересечение с каждой сканирующей прямой. Далее, используя алгоритм Брезенхема и одновременно генерируя растровое представление для ребер левой и правой части ломаных границ, получаем левый и правый пиксели границы многоугольника на каждой сканирующей горизонтальной прямой. Последовательно заполняя интервалы между этими пикселами для каждого значения ординаты от верхней строки развертки до нижней, получим растровое представление многоугольника. Блок-схему этого алгоритма можно посмотреть на странице графики (алгоритм генерации растрового представления выпуклого многоугольника построчным сканированием). Один частный случай этого алгоритма получил широкое распространение в связи с задачами трехмерной графики, это закраска треугольника. В этом случае можно существенно упростить алгоритм.
Алгоритм закраски произвольной области с затравкой
Рассмотрим еще один класс алгоритмов "закраски", а именно алгоритмы заполнения области с затравкой. В этих алгоритмах предполагается, что граница области задана на растровой плоскости и указана одна из внутренних точек области, которая называется затравочной. Требуется заполнить определенным цветом связную компоненту области, содержащую затравочную точку. Под связностью будем понимать 4-х или 8-ми связности, определенные выше (какая связность конкретно используется, зависит от формулировки задачи).
Данному классу алгоритмов можно сопоставить физическую интерпретацию, а именно представить, что в затравочной точке помещен источник, заливающий всю область определенным цветом. Поэтому часто такие алгоритмы называют алгоритмами заливки.
В связи с той физической интерпретацией, которую мы имеем, можно получить очевидный алгоритм решающий задачу заливки области. Допустим нам надо "закрасить" цветом IColor область, граница, которой имеет цвет BColor, и нам задана точка с координатами (x0 , y0 ) в качестве затравочной.
- Поместим затравочную точку на стек.
- Извлекаем координаты точки с вершины стека в переменные x, y
- Если Screen[x,y] <> IColor, то Screen[x,y] = IColor
- Для всех соседних точек (xg, yg) повторить пункт 5
- Если Screen[xg,yg]<>BColor и Screen[xg,yg]<>IColor, то поместить точку (xg, yg) на стек.
- Если стек не пуст, то переходим к пункту 3.
Соседние точки, пункта 4 алгоритма, определяются в зависимости от того, какое условие связности определенно в условие задачи.
Приведенный алгоритм весьма неэффективен, так как предполагает неоднократную обработку одних и тех же точек и неконтролируемый рост размера стека. Поэтому усовершенствуем его, используя идею, примененную нами в алгоритме построчного сканирования.
Заметим, что на каждой строке множество точек подлежащих закраске, состоит из интервалов, принадлежащих внутренности области. Эти интервалы отделены друг от друга интервалами из точек, принадлежащих границе или внешности области. Кроме того, если набор точек образует связный интервал, принадлежащий внутренней части области, то точки над и под этим интервалом либо являются граничными, либо принадлежат внутренней части области. Последние могут служить затравочными для строк лежащих выше и ниже рассматриваемой строки. Суммируя все это, можно предложить следующий алгоритм.
- Поместим затравочную точку на стек.
- Извлекаем координаты точки с вершины стека в переменные (x, y)
- Заполняем максимально возможный интервал, в котором находится точка, вправо и влево вплоть до достижения граничных точек.
- Запоминаем крайнюю левую xl и крайнюю правую xr абсциссы заполненного интервала.
- В соседних строках над и под интервалом (xl , xr ) находим незаполненные к настоящему моменту внутренние точки области, которые объединены в интервалы, а в правый конец каждого такого интервала помещаем на стек.
- Если стек не пуст, то переходим к пункту 3.
Алгоритм правильно заполняет любую область даже такую сложную как на рисунке:

Более подробно структуру алгоритма можно рассмотреть при помощи блок-схемы, которая есть на странице графики (алгоритм закраски области с затравкой). На этом я заканчиваю данную статью. Я рассмотрел наиболее часто используемые алгоритмы, если они Вас заинтересовали, пишите мне, задавайте вопросы, может быть эта тема получит продолжение.
Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU