|
|
| Обозначение |  |
| Область значений |  |
| Параметры | Количества
степеней свободы – целые положительные числа  и
и 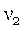 , параметры
формы. , параметры
формы. |
| Плотность |
 |
| Математическое ожидание |
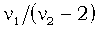 , , 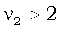 |
| Дисперсия |
 , , 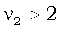 |
| Функция распределения | Не выражается в элементарных функциях |
 и бета-распределение
и бета-распределение  связаны следующим соотношением
связаны следующим соотношением  =
= .
. )-квантиля
распределения
)-квантиля
распределения  есть величина, обратная
есть величина, обратная  -квантилю
распределения
-квантилю
распределения  .
То же самое формулой:
.
То же самое формулой: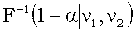 =
= ,
,
здесь, как и всюду -1 в качестве верхнего индекса говорит об обратной функции.
 ,
,  две независимые случайные величины с n1
и n2
степенями свободы соответственно, то
две независимые случайные величины с n1
и n2
степенями свободы соответственно, то  ~
~ .
Это соотношение – один из основных источников применения F-распределения,
а также причина еще одного его названия, распределение дисперсионного
отношения: ведь при применении дисперсионного анализа принято считать,
что исходные наблюдения распределены нормально и, значит, дисперсии подчиняются
распределению
.
Это соотношение – один из основных источников применения F-распределения,
а также причина еще одного его названия, распределение дисперсионного
отношения: ведь при применении дисперсионного анализа принято считать,
что исходные наблюдения распределены нормально и, значит, дисперсии подчиняются
распределению  .
.Вот статистическая переформулировка
последнего свойства. Пусть даны два набора независимых в совокупности нормальных
случайных величин: 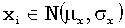 ,
i=1..nx,
,
i=1..nx,  ,
i=1..ny. Определим случайные
величины
,
i=1..ny. Определим случайные
величины  ,
,  ,
,  и
и  следующим образом:
следующим образом:
 ,
,  ,
, 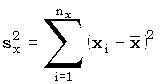 ,
,  .
.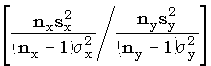 подчиняется F-распределению
с параметрами nx
и ny.
подчиняется F-распределению
с параметрами nx
и ny.
Методы, специфические для данного распределения, мне неизвестны.
Проще всего использовать указанную связь с бета-распределением.
Для вычисления с помощью
нижеследующих кодов потребуются файлы betaDF.h
и betaDF.cpp (их описание см. в тексте о бета-распределении,
а также logGamma.h
и logGamma.cpp (см. Приложение А).
#ifndef __FDF_H__ /* To prevent redefinition */ #define ENTRY extern #define LOCAL static double FDF(double n1, double n2, double x); /* Вычисляет вероятность того, что случайная величина, * подчиняющаяся центральному F-распределению с параметрами n1 и n2, * не превосходит заданного значения x. */ double inv_FDF(double n1, double n2, double p); /* Ищет точку, в которой функция F-распределения * с параметрами n1 и n2 равняется p */ #define __FDF_H__ /* Prevents redefinition */ #endif /* Ends #ifndef__FDF_H__ */ |
#include <math.h>
#include <assert.h>
#include "betaDF.h"
ENTRY double
FDF(double n1, double n2, double x)
// Вычисляется вероятность того, что случайная величина,
// подчиняющаяся центральному F-распределению с параметрами n1 и n2,
// не превосходит заданного значения x.
{
assert(x >= 0.0);
return 1.0 - BetaDF(0.5 * n2, 0.5 * n1).value(n2 / (n2 + n1 * x));
}/*FDF*/
ENTRY double
inv_FDF(double n1, double n2, double p)
// Ищет точку, в которой функция F-распределения
// с параметрами n1 и n2 равняется p
{
double y=BetaDF(0.5 * n1, 0.5 * n2).inv(p);
return n2*y/n1/(1-y);
}/*inv_FDF*/
|
Дата последней модификации: 29 апреля 2000 г.