|
|
|
Обозначение |
|
| Область значений: |
|
|
Параметры |
Параметры формы: a,b > 0. |
| Плотность |
 , где , где 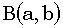 – (полная) бета-функция от параметров a и b. – (полная) бета-функция от параметров a и b. |
| Математическое ожидание | a/(a+b) |
| Дисперсия |
 |
| Функция распределения | Не выражается в элементарных функциях |
Полезные свойства
Нет, пожалуй, другого такого распределения, которое встречалось бы в математической статистике столь же часто, как бета-распределение. Достаточно сказать, что его специальным случаем является F-распределение! А именно, функция распределения так называемого F-отношения  выражается формулой
выражается формулой
 .
.
Отсюда следует, что при 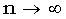 бета-распределение сходится к гамма-распределению.
бета-распределение сходится к гамма-распределению.
Вот еще несколько любопытных частных случаев.

А вот знаменитое свойство симметрии бета-распределения: 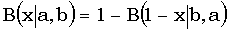 .
.
При разных значениях параметров функция распределения имеет самые разные свойства. На нижеследующем рисунке приведены графики плотности бета-распределения при нескольких значениях параметров.
Пусть случайные числа
r1 и
r2
независимы и распределены равномерно на отрезке
[0,1].
Положим 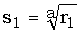 ,
,
 .
Если s1+s2 > 1,
повторим вычисления. Если же
s1+s2
.
Если s1+s2 > 1,
повторим вычисления. Если же
s1+s2
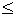 1, то
r = s1/(s1+s2)
подчиняется бета-распределению с параметрами
a и
b.
1, то
r = s1/(s1+s2)
подчиняется бета-распределению с параметрами
a и
b.
Стандартное разложение плотности в ряд Тейлора и почленное интегрирование приводит к степенному ряду

 ,
,
который фигурирует во всех текстах про бета-распределение. Этот ряд сходится довольно медленно. Кроме того, когда a и b велики (что требуется при применения F-распределения к большим выборкам), может возникнуть переполнение. Другие разложения в ряд можно найти в горячо рекомендуемом справочнике М.Абрамовица и И.Стигана "Справочник по специальным функциям", М: Мир 1979.
Гораздо более полезным оказалось разложение неполной бета-функции в цепную дробь
 ,
,
где
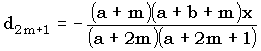 ,
,  .
.
Характер сходимости ее подходящих дробей достаточно сложен, поскольку члены ее звеньев альтернируют. Однако, как часто бывает, четные подходящие дроби ведут себя очень даже пристойно, монотонно сходясь к нужному пределу. Поэтому в нижеследующих кодах в цикле вычисляются две последовательные подходящие дроби: это позволяет в условиях останова иметь дело лишь с четными номерами. Сходимость высока при ![]() , в худшем случае потребуется просуммировать
, в худшем случае потребуется просуммировать ![]() подходящих дробей. Если же
подходящих дробей. Если же ![]() , естественно использовать симметрию бета-распределения.
, естественно использовать симметрию бета-распределения.
Для поиска квантилей используется бисекция – метод деления пополам.
Приводимые коды следует, естественно, рассматривать лишь как иллюстрацию, хотя и работоспособную во всех статистических задачах, с которыми я сталкивался. Если же задача состоит в разработке методов вычисления одной из специальных функций – неполной бета-функции, то придется учитывать разнообразные частные случаи (например, очень маленькие или очень большие значения параметров a и b, соотношение между x и параметрами a и b и т.п.). Для работы с приводимыми здесь кодами необходимы функции, содержащиеся в файлах logGamma.h и logGamma.cpp (описание см. в Приложении А).
/***********************************************************/
/* Beta distribution */
/***********************************************************/
#ifndef __BETA_H__ /* To prevent redefinition */
#define ENTRY extern
#define LOCAL static
class BetaDF {
public:
BetaDF(double u, double w);
double value(double x); // Функция распределения Beta(x|a,b)
double inv(double p); // Обратная функция: Beta(x|a,b)=p
private:
double a,b, logBeta;
double fraction(double a, double b, double x);
};
#define __BETA_H__ /* Prevents redefinition */
#endif /* Ends #ifndef __BETA_H__ */
|
/***********************************************************/
/* Бета-распределение */
/***********************************************************/
#include <math.h>
#include <assert.h>
#include "BetaDF.h"
#include "logGamma.h"
BetaDF::BetaDF(double u, double w):
a(u), b(w), logBeta(logGamma(a) + logGamma(b) - logGamma(a + b))
{
assert(a > 0 && b > 0);
}
double
BetaDF::fraction(double a, double b, double x)
//
// См. Abramowitz & Stegun,
// Handbook of Mathematical Functions, 1964 [26.5.8]
// М.Абрамовиц, И.Стиган
// Справочник по специальным функциям (М: Мир, 1979)
//
// Неполная бета-функция вычисляется с помощью разложения в цепную дробь
//
// i_beta(a,b,x) = x^{a}*(1-x)^{b}*fraction / a * beta(a,b),
// где
//
// 1 d1 d2 d3 d4
// fraction = --- ---- ---- ---- ---- ....
// 1+ 1+ 1+ 1+ 1+
//
// Подходящие дроби: A(n) / B(n)
//
// где
// A(n) = (s(n) * A(n-1) + r(n) * A(n-2)) * factor
// B(n) = (s(n) * B(n-1) + r(n) * B(n-2)) * factor
// и
// A(-1) = 1, B(-1) = 0, A(0) = s(0), B(0) = 1.
//
// Здесь s(0) = 0 и при n >= 1 s(n) = 1,
// а r(1) = 1 и при i >= 2
//
// r(i) = m(b-m)x / (a+i-1)(a+i) когда i = 2m,
// r(i) = -(a+m)(a+b+m)x / (a+i-1)(a+i) когда i = 2m+1,
//
// factor - шкалирующий множитель, позволяющий избежать переполнения.
//
// Итак, A(0) = 0 , B(0) = 1,
// r(1) = -(a+b)*x / (a+1)
// A(1) = A(0) + r(1)*A(-1) = r(1) = 1
// B(1) = B(0) + r(1)*B(-1) = 1
//
{
double old_bta = 0, factor = 1;
double A0 = 0, A1 = 1, B0 = 1, B1 = 1;
double bta = 1, am = a, ai = a;
double iter = 0, r;
do {
// часть цикла, вычисляющая нечетные подходящие дроби
// начинаем с i = 1, iter = 0
ai += 1; // = a+i
r = -am * (am + b) * x / ((ai - 1) * ai);
/* пересчет A и B в два шага */
A0 = (A1 + r * A0) * factor; /* i НЕчетно */
B0 = (B1 + r * B0) * factor;
// часть цикла, вычисляющая нечетные подходящие дроби
// начинаем с i = 2, iter = 1
am += 1;
iter += 1;
ai += 1;
r = iter * (b - iter) * x * factor / ((ai - 1) * ai);
A1 = A0 + r * A1; /* i четно, A0 и B0 уже шкалированы */
B1 = B0 + r * B1;
old_bta = bta;
factor = 1 / B1;
bta = A1 * factor;
} while (fabs(old_bta) != fabs(bta));
return bta * exp(a * log(x) + b * log(1 - x) - logBeta) / a;
}/*incBeta_fraction*/
double
BetaDF::value(double x)
//
// Вычисляет Beta(x|a,b):
// вероятность того, что случайная величина,
// подчиняющаяся бета-распределению с параметрами 'a' и 'b',
// меньше или равна 'x'.
//
{
if (x <= 0)
return 0; /* НЕ ошибка! */
else if (x >= 1)
return 1; /* НЕ ошибка! */
if (x < (a + 1) / (a + b + 2))
return fraction(a, b, x);
else
return 1 - fraction(b, a, 1 - x);
}/*value*/
double
BetaDF::inv(double p)
//
// Ищет такое значение 'x', для которого Beta(x|a,b) = p,
// т.е. равна 'p' вероятность того, что случайная величина,
// подчиняющаяся бета-распределению с параметрами 'a' и 'b',
// меньше или равна 'x'.
//
{
double fx, l = 0, r = 1, x = 0.5;
assert(p >= 0 && p <= 1);
if (p == 0 || p == 1) return p;
do {
fx = value(x);
if (fx > p) r = x; else
if (fx < p) l = x; else
return x;
x = (l + r)* 0.5;
} while ((l!=x) && (r!=x));
return x;
}/*inv*/
|
Дата последней модификации: 25 октября 2000 г.