|
4 тур - з 27.11 по 03.12.2017
точка входу для відправлення розв’язків
http://134.249.159.199/cgi-bin/new-client?contest_id=46
(скачати)
ЗАДАЧА 1. xOr (20 балів)
Ім’я вхідного файлу: input.txt
Ім’я вхідного файлу: output.txt
Ліміт часу: 1с.
Мало хто знає про існування такої країни як Кеклядія (воно і не дивно). З космосу Кекляндія представляє собою квадратну матрицю чисел розміром N*N.
Король країни полюбляє збирати податки, при чому він робить це доволі специфічним чином.
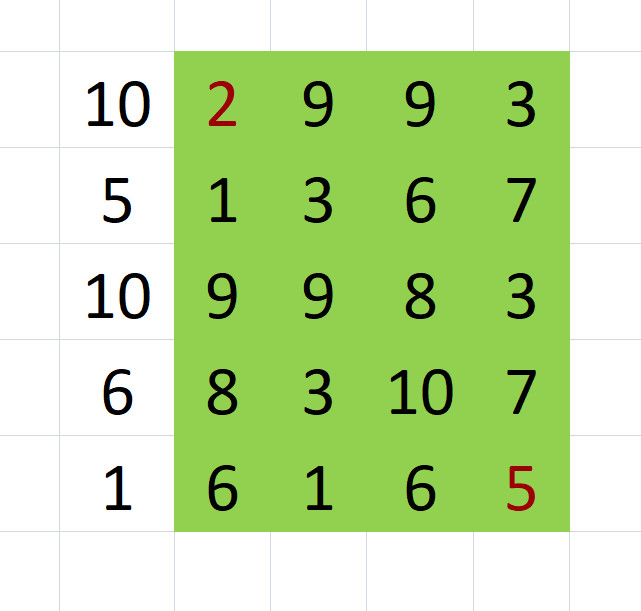
Він вибирає дві довільні точки, які є кутніми в деякому прямокутнику. Тоді загальним податком є побітовий XOR чисел, які належать даному прямокутнику.
Один з можливих випадків наведено на малюнку(зеленим кольором виділено числа, які потрібно проXORирити, червоний текст - вибрані точки).
Після збору податків числа в самій матриці не змінюються.
Вхідні дані
В першому рядку знаходиться одне число - N (1≤ N≤ 1000).
В наступних N рядках знаходиться по N чисел, які утворюють квадратну матрицю, кожне з яких менше за 10^9.
В наступному рядку знаходиться M (1≤ M≤ 1000000).
В наступних М рядках знаходиться по 4 числа - координати точок, які король вибрав для збору податків.
Вихідні дані
В кожному окремому рядку вивести податок, який потрібно заплатити, для кожної пари точок.
Приклад,
|
Вхідні дані
|
Вихідні дані
|
|
5
10 2 9 9 3
5 1 3 6 7
10 9 9 8 3
6 8 3 10 7
1 6 1 6 5
5
1 2 5 5
1 3 1 4
4 2 5 4
1 1 1 1
1 2 2 3
|
11
0
0
10
9
|
ЗАДАЧА 2. Мишка і Зернинки (100 балів)
Ім’я вхідного файлу: input.txt
Ім’я вхідного файлу: output.txt
Ліміт часу: 8с.
Вам задана матриця N*N і два цілих числа - K і M. Елементи матриці визначаються наступним чином: Aij=(K*i*i*j) остача (mod, %) M, 1≤i,j≤N.
На початку ви знаходитесь в верхньому лівому кутку матриці. Вам потрібно попасти в правий нижній куток. Ходити можна тільки вправо і вниз.
Ваше завдання - знайти шлях мінімальної вартості. Якщо таких шляхів декілька, то в момент коли є вибір ходити вниз або вправо, необхідно ходити вправо.
Вхідні дані
В єдиному рядку знаходиться три цілих числа N, K, M (1≤N≤10000, 1≤K, M≤1000000000)
Вихідні дані
В першому рядку вивести 1 число - мінімальну суму чисел шляху.
Далі потрібно вивести (2*N-1) рядків. Кожний рядок повинен містити по 2 числа - координати кожної наступної клітинки на шляху.
Приклад
|
Вхідні дані
|
Вихідні дані
|
|
5 2 7
|
21
1 1
2 1
2 2
3 2
4 2
5 2
5 3
5 4
5 5
|
|

