Сайт підготовки до олімпіади з інформатики
програмування в С++
| Завдання з теми Теорія графів |
 |
 |
 |
| Добавил(а) Administrator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11.03.11 13:48 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Прізвище ______________
Завдання на міні-олімпіаду
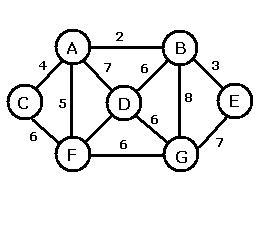
1. За заданими малюнком (20 балів)
а) задайте матрицю суміжності
б) знайти ейлеровий шлях; _________________________________________________ в) знайти гамільтонів шлях; ________________________________________________ г) знайти найкоротший гамільтонів шлях; ____________________________________ г) написати програму, яка за описаним графом, виводила довжину ейлеревого шляху, якщо він існує, якщо шлях не існує виводить повідомлення NO. д) написати алгоритм пошуку та виведення всіх шляхів з вершини I вершину J для графу заданого на малюнку вище.
2. Задача 1. (30 балів , алгоритм Флойда) Вхідні дані задані у файлі Graph.dat у вигляді 1 рядок – N – кількість ребер, M – кількість вершин (M<=100, N<=10000) , наступні N рядків задають і, j вершини і довжину ребра aij (aij<=10000). У файл Graph.sol вивести найкоротшу довжину з вершини I в вершину J в форматі I J Dij, та повідомлення NO, якщо шляху не існує.
3. Задача 2. (50 балів , алгоритм Прима) Збирання мита. Король країни Аріїв завоював N міст на території сусідніх держав. Тепер йому необхідно створити систему збирання мита з завойованих територій. Він хоче збудувати таку систему шляхів між цими містами, щоб до будь-якого міста можна було дістатися (можливо, через інші міста) зі столиці, але у воєнному стані на транспорт виділяється дуже незначна частина фінансів, тому сумарна вартість побудованих шляхів сполучення між містами має бути мінімальною. Вхідні дані: Перший рядок вхідного файлу містить натуральне число N (1<=N<=100) – кількість міст у країні, а також цілі числа X та Y – координати столиці. Наступні N рядків містять через проміжок координати Xi , Yi завойованих міст. Значення координат по модулю менші 50000. Вихідні дані: Перший рядок має містити дійсне число з трьома знаками після коми – сумарну вартість побудованих доріг. Вважайте, що вартість одиниці довжини дороги дорівнює одній умовній одиниці. Наступні рядки мають містити у довільному порядку список побудованих доріг у форматі: => При цьому столицю позначте номером 0. Якщо відповідей декілька, виведіть одну довільну з них. Приклади:
Додаткова задача. 4. Відомий всім форт Буайяр пропонує своїм відвідувачам таке випробування: піднятися по досить нахиленій слизькій площині вгору, щоб дістати ключ. На площині розміщені невеличкі виступи, кожний виступ настільки малий, що поміститися на ньому може лише одна нога. Домовимося, що під час пересування по площині гравець не може перехрещувати ноги (ліву за праву і навпаки). Нехай L максимальна довжина кроку гравця, п — кількість виступів, (хi; yj)і = 1,2, ..., п — координати виступів на площині. Вважатимемо, що початкове положення гравця: х0 > О, у0 = 0 (стартує з будь-якого місця на підлозі). Визначте всі можливі найменші за кількістю кроків варіанти (якщо вони існують) послідовностей номерів виступів, по яких необхідно рухатись гравцю, чергуючи ноги, щоб дістатися самого верхнього виступу. Вкажіть, з якої ноги йому починати рух. Всі вхідні дані вважати цілими числами.
|
Статистика
Пользователей : 290Статей : 225
Просмотрено статей : 153979