Сайт підготовки до олімпіади з інформатики
програмування в С++
| Методика підготовки до олімпіади (навчаємось постійно) |
 |
 |
 |
| Добавил(а) Гісь Ігор Володимирович | ||||||||||||||||||||||||||||||
| 11.06.13 11:19 | ||||||||||||||||||||||||||||||
|
Тематика
1. Олімпіадна інформатика 2. Тематика завдань 3. Системи тестування (ejudge, e-olymp, Contester ) 4. Оптимізація розв’язку (прості числа, лічилка) 5. Довга арифметика (факторіал, фібоначі) 6. Повний перебір (лексичний перебір) 7. Обчислювальна геометрія (ліві повороти, площа многокутника) 8. Теорія графів (пошук в глибину, остове дерево, алгоритм флойда) 9. Практикум з розв’язування задач
1.Олімпіадна інформатика Що потрібне для успішної участі в олімпіадах по інформатиці? Як показує практика, тільки знання мови програмування для цього явно не достатньо. Взагалі, виявляється, що олімпіадні задачі по інформатиці лежать десь на стику математики і програмування. І дуже часто виявляється, що розв’язуючи задачі школярі не тільки вчаться програмувати, але і освоюють нові розділи математики. Як перевіряються розв’язки задач олімпіади Історично склалося так, що розв’язки на олімпіадах по програмуванню перевіряються автоматично. Ваше завдання написати програму, яка за заданими вхідними даними обчислює і виводить вихідні дані. Апаратне та програмне забезпечення Учасникам олімпіади можуть вибирати мову програмування с заданого переліку: Pascal, C або C++. Система програмування Free Pascal 2.0 (чи новішої версії), GCC 4.2 (чи новішої версії), Turbo Delphi Explorer, Visual C++ 2008 Express).
2. Тематика задача олімпіади Завдання олімпіади мають бути алгоритмічного характеру, тобто основними результатами роботи учасника має бути: алгоритм, що правильно та ефективно розв’язує поставлену задачу, та програма, що реалізує запропонований алгоритм. Основними категоріями олімпіадних задач є:
3.Системи тестування (ejudge, e-olymp, Contester ) Працюйте в он-лайн системах, які автоматично перевіряють та тестують Ваші розв’язки: http://olymp.sumdu.edu.ua - Веб-ресурс підтримки та проведення шкільних та студентських олімпіад з інформатики http://www.e-olimp.com.ua/ - Інтернет-портал організаційно-методичного забезпечення дистанційних олімпіад з програмування для обдарованої молоді навчальних закладів України http://www.olymp.vinnica.ua/ - Центр підтримки та проведення олімпіад школярів з використанням можливостей Internet. Список тестуючи систем
Список ресурсів http://vippolabinfo.16mb.com – сайт «Лабораторія інформатики сьогодні», методична підтримки напрямків роботи. http://vippoolimp.16mb.com – Волинська учнівська Інтернет олімпіада з програмування. http://schoololymp.byethost32.com – заочна школа роботи з обдарованими учнями з інформатики. 4. Оптимізація розв’язку (прості числа, лічилка)
5.Довга арифметика (факторіал, фібоначі)
6.Повний перебір (лексичний перебір) Побудуємо лексичний перебір для довільних елементів масиву X=3 2 4 2 4 3 1 а) Рухаємось справа наліво. Крок вперед можна зробити, якщо наступне число більше за попереднє. Ми зупинилися перед числом 2. Це число потрібно помітити. X=3 2 4 2 4 3 1 б) Рухаємось справа наліво. Крок вперед можна зробити, якщо число менше за знайдене число(2). Ми зупинилися перед числом 3. Це число потрібно помітити. X= 3 2 4 2 4 3 1 в) Переставляємо знайдені числа. X= 3 2 4 3 4 2 1 г) Запишемо числа, розміщені після першого знайденого в зворотному порядку. X=3 2 4 3 1 2 4 7.Обчислювальна геометрія (ліві повороти, площа многокутника) Ліві повороти {Визначення координат векторів}
За заданими кількістю вершин і координатами n-кутника визначити його площу (15 балів). x[n+1]=x[1] y[n+1]=y[1] s=0 для i=1 дo n s=s+ (x[i]*y[i+1]-x[i+1]*y[i] s=1/2*abs(s); 8.Теорія графів (пошук в глибину, остове дерево, алгоритм флойда)
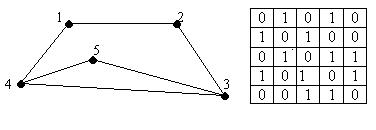
1. Граф представляє собою не порожню множину точок і ліній, два кінці котрих належать заданій множині точок. Неорієнтований граф:
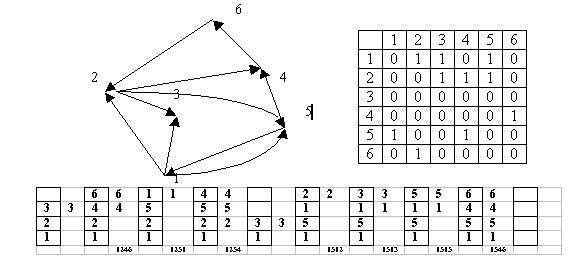
Відкриті Ейлером властивості графа: 1. Число непарних вершин зв'язного графа завжди парне. Неможливо накреслити граф з непарним числом непарних вершин. 2. Якщо всі вершини графа парні, то можна одним розчерком (тобто не відриваючи олівця від паперу) накреслити граф, не проводячи по кожному ребру більше одного разу. При цьому можна починати з будь-якої вершини графа і закінчувати його в тій же вершині. 3. Граф лише з двома непарними вершинами можна накреслити одним розчерком, при цьому рух потрібно почати в одній точці з цих вершин і закінчити в другій непарній вершині. 4. Граф з більше ніж двома непарними вершинами неможливо накреслити одним розчерком. Гамільтонів шлях проходить через кожну вершину по одному разу (по ребрах проходить декілька разів або жодного) Ейлеровий шлях – це шлях, який ми проходимо з однієї вершини в іншу через всі ребра тільки один раз. Задача про туриста (пошук в глибину) Турбаза мала для ночівлі N місць, з’єднаних стежками. Туристів можна вести в одну сторону. Довжина стежки – одноденний перехід. Пройти і перевірити всі M-денні маршрути, які починаються на базі K. Орієнтований ненавантажений граф. n=6; m=3; k=1;
Дано орієнтований ненавантажений граф. N вершин. Знайти всі маршрути довжини m=3, які виходять з вершини з номером k. Алгоритм Флойда-Уоршелла З алгоритму Дейкстри зрозуміло, що можна знайти найкоротшу відстань від заданої вершини графа до решти його вершин. А якщо ця інформація потрібна для будь-якої вершини графа? Найперша відповідь, яка спадає на думку: необхідно виконати алгоритм Дейкстри в циклі для всіх вершин графа. Питання лише в часі виконання такого алгоритму, оскільки його оцінка буде О(п3). Однак існує компактніший за записом алгоритм Флойда-Уоршелла, з яким ми зараз і ознайомимося. Запишемо сам алгоритм: 1. Визначити вершину графа k = 1, через яку буде здійснюватися перерахунок відстані між вершинами і та j. 2. Визначити вершину і = 1. Визначити вершину j = 1, 3. Якщо величина dj, k + dk,j менша за значення di,j ,то замінити значення di,j на di, k + dk,і . В іншому разі залишити значення di,j без змін. 4. Якщо j <= п, то перейти до наступної вершини j+ 1 і повернутися до п. 4. 5. Якщо i<= п, то перейти до наступної вершини і + 1 і повернутися до п. 3. 6. Якщо k<=n, то перейти до наступної вершини k + 1 і повернутися до п. 2, 7. Завершити алгоритм. У результаті виконання алгоритму елементи di,j будуть містити найкоротшу відстань між відповідними вершинами графа і та j. Реалізація алгоритму Флойда-Уоршелла мовою Pascal буде такою: for k := 1 to n do for і := 1 to n do for j := 1 to n do if d[i,k]+d[k,j]<d[i,j] then d[i,j]:=d[i, k]+d[k,j];
9.Практикум з розв’язування задач http://nvk26.lutsk.ua/cgi-bin/new-client?contest_id=3 – ІІ етап (районний) Всеукраїнської олімпіади з інформатики 2012-2013 н.р. (логін user400-user430; пароль 400-430). http://nvk26.lutsk.ua/cgi-bin/new-client?contest_id=11 – ІІІ етап (обласний) Всеукраїнської олімпіади з інформатики 2012-2013 н.р. (логін user400-user430; пароль 400-430). http://nvk26.lutsk.ua/cgi-bin/new-client?contest_id=12 – тренувальний тур по підготовці до ІV етапу Всеукраїнської олімпіади з інформатики 2012-2013 н.р. (логін user400-user414; пароль 400-414). |
||||||||||||||||||||||||||||||
| Последнее обновление 11.06.13 11:38 |
Статистика
Пользователей : 290Статей : 225
Просмотрено статей : 154104
 Основні поняття теорії графів
Основні поняття теорії графів