1.2 МАССИВЫ. 

Задача 1. Дан массив х: array[1..n] of integer, причем x[1]<=x[2]<=...<=x[n]. Найти количество различных чисел среди элементов массива. 

Решение: 
      i:=1; k:=1;
      while i<>n do
        begin
          i:=i+1;
          if x[i]<>x[i-1] then k:=k+1;
        end;

Другой вариант решения:
      k:=1;
      for i:=1 to n-1 do 
        if x[i]<>x[i+1] then k:=k+1; 

Задача 2. Дан массив x: array[1..n] of integer. Найти количество различных чисел среди элементов этого массива. Число действий  должно быть порядка n^2. 

Решение: 
      k:=0; 
      for i:=1 to n do 
        begin 
          j:=i+1;y:=true; 
      while (j<=n) and (y) do 
            if x[j]=x[i] then y:=false else j:=j+1; 
          if y then k:=k+1; 
        end; 
Не трудно посчитать, что число действий порядка n·n. 

Задача3. Дан массив x: array[1..n] of integer. Не используя других массивов, переставить элементы массива в обратном порядке. 

Решение: Каждый i-й элемент нужно поменять с (n+1-i)-м элементом местами. Для которых i<n+1-i, то есть 2i<n+1  <=>  2i<=n  <=>  i<= n div 2. 

      for i:=1 to n div 2 do 
        begin 
             k:=x[i]; x[i]:=x[n+1-i]; x[n+1-i]:=k; 
        end; 

   Многочленом от одной переменной x будем называть выражение вида 
   P_n(x)=a₀·xⁿ+a₁·x^n-1+...+a_n-1·x+a_n. 
   Например: P(x)=3·x⁴+5·x³-2·x+6. 
  Схема Горнера - прием для нахождения неполного частного и остатка при делении многочлена P_n(x) на двучлен (x-c). 
   Всякий многочлен единственным способом представим в виде 
   Pn(x)=(x-c)Q_n-1(x)+R, где Q_n-1(x)=b₀· x^n-1+...+b_n-2·x+b_n-1 - неполное частное, а R - остаток. Коэффициенты многочлена Q_n-1 и R  вычисляются по рекуррентным формулам 
   b₀=a₀, b₁=a₁+c·b₀, ..., b_n-1=a_n-1+c·b_n-2, R=a_n+c·b_n-1. 
Например: Найдем  частное  Q(x)  и  остаток  R  при  делении  многочлена 
(x)=2·x⁵-x⁴-3·x³+x-3 на многочлен T(x)=x-3. 
Пользуясь реккурентными формулами получим: 
2·x⁵-x⁴-3·x³+x-3=(x-3)(2·x⁴+5·x³+12·x²+36·x+109)+324. 
   В вычислительной практике алгоритм Горнера осуществляется при помощи   формулы P_n(x)=a₀+x·(a₁+x·(a₂+...+x·(a_n-1+x·a_n)...)). 
(см. Математический энциклопедический словарь; М.К.Потапов, В.В.Александров, П.И. Пасиченко ⌠Алгебра и анализ элементарных функций■ стр.86). 
  
Задача 4. Коэффициенты многочлена лежат в массиве a: array[0..n] of integer (n - натуральное число, степень многочлена). Вычислить значение  многочлена в точке x, то есть 
          a[n]xⁿ + ...+ a[1]x + a[0] . 

Решение: Для 0<=k<=n вычисляем y=a[n]·x^k+a[n-1]·x^k-1+..+a[n-k]·x⁰. 
         Воспользуемся схемой Горнера. Тогда значение многочлена будет равно 
         y=(...((a_n·x+a_n-1)·x+a_n-2)·x+...+a₁)·x+a₀ 
  
      k:=0; y:=a[n]; 
      while k<>n do 
        begin 
          k:=k+1; 
          y:=y·x+a[n-k]; 
        end; 

Задача 5. Даны два возрастающих массива x: array[1..k] of ihteger и  y: array[1..h] of ihteger.Найти количество общих элементов в этих массивах, то есть количество тех элементов, для которых  x[i]=y[j] для некоторых i и j. Число действий порядка k+h. 

Решение: Возьмем дополнительные переменные 0<=k1<=k и 0<=h1<=h. 
       Искомое количество общих элементов будем хранить в n. 

      k1:=0; h1:=0; n:=0; 
      while (k1<>k) and (h1<>h) do 
        if x[k1+1]<y[h1+1] 
          then k1:=k1+1 
            else if x[k1+1]>y[h1+1] 
                   then h1:=h1+1 
                     else begin k1:=k1+1; h1:=h1+1; n:=n+1; end; 

Цикл повторяется k+h раз. В теле цикла выполняется или одна, или три операции присваивания. В любом случае число действий порядка k+h. 

Задача 6. Даны два массива x[1]<=...<=x[k] и y[1]<=...<=y[h]. "Соединить" их в массив z[1]<=...<=z[m] (m=k+h, каждый  элемент должен входить в массив z столько раз, сколько раз он входит в общей сложности в массивы x и y). Число  действий порядка m. 

Решение: Пусть у нас есть две стопки карточек, отсортированных по алфавиту. Мы соединяем их в одну стопку, выбирая каждый раз ту из верхних карточек обеих стопок, которая идет  раньше в алфавитном порядке. Если в одной стопке карточки        кончились, берем их из другой стопки. 

      k1:=0; h1:=0; 
      while (k1<>k) or (h1<>h) do 
        if k1=k then begin h1:=h1+1; 
                           z[k1+h1]:=y[h1] end 
          else 
            if h1=h then begin k1:=k1+1; 
                               z[k1+h1]:=x[k1] end 
              else 
                if x[k1+1]<=y[h1+1] then begin k1:=k1+1; 
                                               z[k1+h1]:=x[k1] end 
                  else 
                    if x[k1+1]>=y[h1+1] then begin h1:=h1+1; 
                                                   z[k1+h1]:=y[h1] end; 

При каждом вхождении в цикл (их m=k+h) выполняется только одно из условий и число операций равно двум. Значит общее число действий - 2m. 

Задача7. Некоторое число содержится в каждом из трех целочисленных         неубывающих массивов x[1]<=...<=x[p], y[1]<=...<=y[q],  z[1]<=...<=z[r]. Найти одно из таких чисел. Число действий   должно быть порядка p+q+r. 

Решение: 
      p1:=1; q1:=1; r1:=1; 
      while not((x[p1]=y[q1]) and (y[q1]=z[r1])) do 
        if x[p1]<y[q1] then p1:=p1+1 
          else 
            if y[q1]<z[r1] then q1:=q1+1 
              else 
                if z[r1]<x[p1] then r1:=r1+1; 
      {x[p1]=y[q1]=z[r1]} 
      writeln(x[p1]); 

Как и в предыдущей задаче число вхождений в цикл равно p+q+r, где выполняется только один оператор присваивания. 

Задача 8. Дан целочисленный массив x[1]<=...<=x[n] и число a. Выяснить, содержится ли a в этой последовательности, то есть найти такое i из 1..n, для которого x[i]=a. 
Количество действий порядка log₂n. 

Решение: Метод двоичного поиска: Рассмотрим отрезок 1..n. Делим его пополам и выбираем ту половину, в которой может находиться такое i, что x[i]=a.  
(см. Н.Вирт ⌠Алгоритмы и структура данных■) 
      q:=1; r:=n;
      while r-q<>1 do
        begin
          m:=(r+q) div 2;
          if x[m]<=a then q:=m else r:=m;
        end;
      if (x[q]=a) or (x[r]=a) then writeln('есть')
        else writeln('нет');

Каждый раз r-q уменьшается примерно вдвое, поэтому количество действий не превосходит 2·log₂ n.

Задача 9. Дан массив x:array[1..n,1..m] of integer, упорядоченный по строкам и по столбцам и число a. Требуется выяснить,  встречается ли a среди x[i,j].

Решение:
 

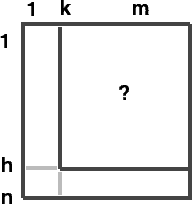Представляя массив как матрицу (прямоугольник, заполненный числами), выберем прямоугольник, в котором только и может содержаться a, и будем его сужать. Прямоугольник этот будет содержать x[i,j] при 1<=i<=h и k<=j<=m.  Допускаются пустые прямоугольники при h=0 и k=m+1.

      h:=n;k:=1;
      while (h>0) and (k<m+1) and (x[h,k]<>a) do
            if x[h,k]<a then k:=k+1 else h:=h-1;
      answer:=(h>0) and (k<m+1);  

Решение: Пусть известно, что числа, представимые ввиде суммы элементов         a[1],...,a[k], заполняют отрезок от 1 до некоторого R. Если  a[k+1]>R+1, то R+1 и будет минимальным числом, не представимым  в виде суммы элементов массива. Если же a[k+1]<=R+1, то числа, представимые в виде суммы элементов a[1],...,a[k+1], заполняют отрезок от 1 до R+a[k+1].

      k:=0;R:=0;
      while (k<>n) and (a[k+1]<=R+1) do
        begin
          R:=R+a[k+1];
          k:=k+1;
        end;
      writeln(R+1);

Очевидно, что число действий не превосходит 2·n.

Задача 11. Дан массив x[1..n] и число b. Переставить числа в массиве  таким образом, чтобы слева от некоторой границы стояли числа, меньшие или равные b, а справа от границы - большие   или равные b.

Решение: 
      h:=0;r:=n;
      while h<>r do
        if a[h+1]<=b then h:=h+1
          else
            if a[r]>=b then r:=r-1
              else begin
                     m:=a[h+1]; a[h+1]:=a[r]; a[r]:=m; 
                     h:=h+1;r:=r-1;
                   end;

УПРАЖНЕНИЯ: 
1.  Решить задачу 5, если известно, что  x[1]<=...<=x[k], y[1]<=...<=y[h]. 
2. Даны два неубывающих массива x: array[1..k] of integer и y: array[1..h] of integer.    Найти количество различных элементов  среди x[1],...,x[k],y[1],...,y[h]. Число     действий порядка k+h.
3. Даны два массива x[1]<=...<=x[k] и y[1]<=...<=y[h]. Найти их ⌠пересечение■, то есть    массив z[1]<=...<=z[m], содержащий их общие элементы, причем кратность каждого    элемента в массиве z равняется минимуму из его кратностей в массивах x,y. Число    действий порядка k+h.
4. Дан массив a[1..n] и число b. Переставить числа в массиве таким образом, чтобы     сначала шли элементы меньшие b, затем равные b, затем большие b.
5. Дана квадратная таблица x[1..n,1..n] и число m<n. Для каждого квадрата m на m в этой таблице вычислить сумму стоящих в нем чисел. Число действий порядка n².
6. В массиве a[1]...a[n]  встречаются по одному разу все целые числа от 0 до n, кроме    одного. Найти пропущенное число за время порядка n и с конечной дополнительной    памятью.
Замечание: При решении задач не использовать сортировки.