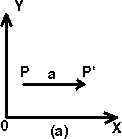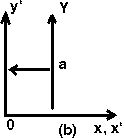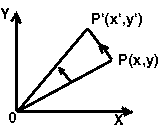В этой теме рассматриваются вопросы аналитической геометрии и программирования в машинной графике. Предполагается, что читатель владеет знаниями по математике в объеме девяти классов средней школы, знает основы языка Turbo Pascal, а также имеет навыки работы в графике.   Преобразование и новые координаты

"Своеобразие геометрии заключается в непрерывном органическом соединении живого воображения со строгой логикой. В ней всегда присутствуют эти два неразрывно связанных элемента: наглядная картина и точная формулировка"

А.Д. Александров

Рассмотрим следующую систему уравнений:

x'=x+a
y'=y

Эти уравнения можно интерпретировать двояким образом:
1. Все эти точки на плоскости xy перемещаются влево на расстояние a - рис. 1(а).
2. Координатные оси x и y перемещаются влево на расстояние a - рис. 1(b).

Рис. 1. (a) - перенос;	(b) - изменение координат

Этот простой пример илюстрирует принцип, применяемый и в более сложных ситуациях. Однако та же самая система уравнений может интерпретироваться и как изменения системы координат.

Рис. 2. Поворот вокруг точки O на угол Ф.

Пусть необходимо повернуть точку P(x, y) вокруг начала координат O на угол Ф. Изображение новой точки на рис. 2 обозначим через P'(x', y'). Существуют четыре числа a, b, c, d, такие, что новые координаты x' и y' могут быть вычислены по значениям старых координат x и y из следующих уравнении:

x'=ax+by
y'=cx+dy                                                           (1.1)

Для получения значений a, b, c, d рассмотрим вначале точку (x,y)=(1,0). Полагая x=1 и y=0 в уравнении (1.1), получим

x'=a
y'=c

Но в этом простом случае, как это видно из рис. 3(a), значения x' и y' равны соответственно cos? и sin?. Тогда будем иметь

a=cos Ф
c=sin Ф

Аналогичным образом из рис. 3(b) следует

b=-sin Ф
d=cos Ф

Тогда вместо системы уравнений (1.1) можем записать

x' = x cos Ф - y sin Ф                                            (1.2)
y' = x sin Ф + y cos Ф

Рис. 3. (a) - отображение точки (1,0);	(b) - отображение точки (0,1)

 

Задача: Начертить 14 стрелок, летящих в направлении против часовой стрелки относительно точки О первого квадранта координатной системы.

Решение:
Приведем решение данной задачи на языке Turbo Pascal.

Uses Crt, Graph;
    type arr=array [0..3] of real;
var
     Gd, Gm, i, j : Integer;
     f, cosf, sinf: real;
     u,v:array [0..3] of integer;
const
     x:arr=(6,6,5.9,6.1);       {начальные координаты стрелки}
     y:arr=(-0.25,0.25,0,0);
begin
     f:=6*pi/180;
     cosf:=cos(f); sinf:=sin(f);
     {подключение графического режима}
     Gd := detect;InitGraph(Gd, Gm, 'd:\turbo7\bgi');
     if GraphResult <> grOk then Halt(1);
     setgraphmode(2);

    for i:=1 to 14 do
     begin
       for j:=0 to 3 do {поворот стрелки}
         begin
           x[j]:=x[j]*cosf -y[j]*sinf;  u[j]:=round(x[j]*50)+100;
           y[j]:=x[j]*sinf+y[j]*cosf;  v[j]:=round(y[j]*50)+100;
         end;
       moveto(u[0],v[0]);
       for j:=1 to 3 do  {рисование повернутой стрелки}
         lineto(u[j],v[j]);
       lineto(u[1],v[1]);
     end;
   CloseGraph;
end.

В приведенной программе изображение стрелки вычерчивается после предварительного поворота вокруг точки O на 6⁰.

Рис. 4 Стрелка в исходной позиции

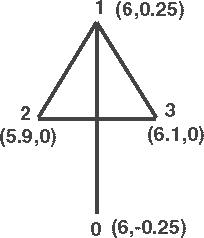
Будем обозначать точки объекта цифрами 0, 1... . В начальной позиции стрелка (рис. 4) указывает вверх, ее центр расположен в точке (6,0).  Значения координат x и y для вершин ломаной линии, изображающей стрелку, записаны в элементах массивов x[i] и y[i] (i=0, 1, 2, 3).
То обстоятельство, что начальное значение y[0] задано отрицательным, а все координаты для вычерчивания должны быть положительными, не вызывает сложностей, поскольку перед вычерчиванием стрелка подвергается повороту, который переносит ее в область над осью x. В массивы u[i] и v[i] записываются округленные значения получаемых координат. Затем они используются для рисования линий (в Turbo Pascal многие графические процедуры работают только с целыми значениями).
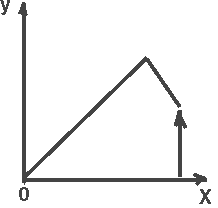
На рисунке показан результат работы этой программы.

Но мы знаем, что система координат на экране монитора расположена в таком виде: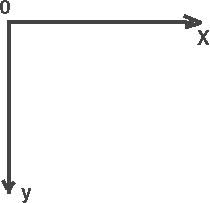

Поэтому наш рисунок получится "летящим" по часовой стрелке. Чтобы этого избежать достаточно поменять знак и сделать параллельный перенос в формулах вычисления координат (подумайте почему):

x[j]:=x[j]*cosf-y[j]*sinf;  u[j]:=round(x[j]*50)+100;
y[j]:=x[j]*sinf+y[j]*cosf; v[j]:=-round(y[j]*50)+350;

Если мы хотим, чтобы на экране "летела" только одна стрелка, то это можно сделать следующим способом:
      moveto(u[0],v[0]);
      for j:=1 to 3 do {рисуем стрелку}
         lineto(u[j],v[j]);
       lineto(u[1],v[1]);
       delay(500);       {делаем задержку}
       setcolor(0); {устанавливаем цвет изображения равный цвету фона}
       moveto(u[0],v[0]);
       for j:=1 to 3 do {рисуем стрелку новым цветом}
         lineto(u[j],v[j]);
       lineto(u[1],v[1]);
       setcolor(15);      {возвращаем цвет изображения}

Система уравнения (1.2) описывает поворот вокруг точки O - начала системы координат. Но часто это не то, что нужно. Если требуется выполнить поворот относительно заданной точки (x0,y0), то в этих уравнениях можно заменить x на x-x0, y - на y-y0, x' - на x'-x0 и y' - на y'-y0:

x'-x0 = (x-x0) cos? - (y-y0) sin Ф
y'-y0 = (x-x0) sin? - (y-y0) cos Ф

(1.3)

x' = x0 + (x-x0) cos? - (y-y0) sin Ф
y' = y0 + (x-x0) sin? - (y-y0) cos Ф

Рассмотрим другие преобразования.
Пусть (x, y) - координаты точки в декартовой системе координат. Тогда
а) при параллельном переносе на d_x единиц по оси x и d_y единиц по оси y координаты меняются так:

x = x-d_x
y = y-d_y

б) при растяжении (сжатии) по оси x в s_x раз и по оси y в s_y координаты меняются так:

x = x *s_x
y = y*s_y

Упражнения:

1. Построить "улитку Паскаля" по параметрическому представлению:

x = a cos²(t) + b cos(t)
y = a sin(t) cos(t) + b sin(t), t принадлежит (0,2Пи), a>0, b>0

после чего выполнить следующие преобразования:
а) перенос по оси X на 10 единиц влево;
б) поворот на угол 45⁰;
в) растяжение по оси Y в два раза.

2. Напишите программу для вычерчивания набора из N  эллипсов, для которых определены параметрические уравнения

x = x₀ + (i∙R/N) cos Ф
y = y₀ + ((N-i)R/N) sin Ф

Возьмите фиксированные значения x₀, y₀, R, N; например, x₀=4, y₀=3.5, R=3, N=40. Пусть i  изменяется в диапазоне от 1 до N-1. Пусть для каждого значения i угол последовательно принимает значения 0⁰, 6⁰, 12⁰, ..., 360⁰.

3. Нарисовать часы (можно без циферблата) с одной секундной стрелкой, которая бежит по часовой стрелке.

Литература:

1. Л. Аммерал. Принципы программирования в машинной графике. -М., Сол Систем, 1992г.
2. В.В. Александров. Рисунок, чертеж, картина на ЭВМ. - Л., Машиностроение, 1987г.
3. Ф.Препарата, М.Шеймос. Вычислительная геометрия: введение. - М., Мир, 1989г.
4. Математический энциклопедический словарь.