Для произвольного слова X рассмотрим все его начала,
одновременно являющиеся его концами, и выберем из них самое
длинное. (Не считая, конечно, самого слова X .) Будем обозначать
его l(X) .
Примеры: 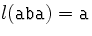 ,
, 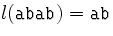 ,
,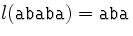 ,
, 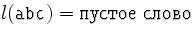 .
.
 10.3.1. Доказать, что все слова l(X) , l(l(X)) , l(l(l(X))) и т.д. являются началами слова X .
10.3.1. Доказать, что все слова l(X) , l(l(X)) , l(l(l(X))) и т.д. являются началами слова X .
Решение. Каждое из них (согласно определению) является
началом предыдущего.
По той же причине все они являются концами слова X .
 10.3.2. Доказать, что последовательность предыдущей задачи обрывается
(на пустом слове).
10.3.2. Доказать, что последовательность предыдущей задачи обрывается
(на пустом слове).
Решение. Каждое слово короче предыдущего.
 10.3.3. Доказать, что любое слово, одновременно являющееся началом
и концом слова X (кроме самого X ) входит в последовательность
10.3.3. Доказать, что любое слово, одновременно являющееся началом
и концом слова X (кроме самого X ) входит в последовательность
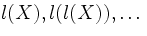
Решение. Пусть слово Y есть одновременно начало и конец
X . Слово l(X) -- самое длинное из таких слов, так что Y
не длиннее l(X) . Оба эти слова являются началами X , поэтому
более короткое из них является началом более длинного: Y есть
начало l(X) . Аналогично, Y есть конец l(X) . Рассуждая по
индукции, можно предполагать, что утверждение задачи верно для
всех слов короче X , в частности, для слова l(X) . Так что
слово Y , являющееся концом и началом l(X) , либо равно
l(X) , либо входит в последовательность
l(l(X)), l(l(l(X))) ,..., что и требовалось доказать.
Алгоритм Кнута-Морриса-Пратта
pvv
1/8/1999
![]() ,
, ![]() ,
,![]() ,
, ![]() .
.![]() 10.3.1. Доказать, что все слова l(X) , l(l(X)) , l(l(l(X))) и т.д. являются началами слова X .
10.3.1. Доказать, что все слова l(X) , l(l(X)) , l(l(l(X))) и т.д. являются началами слова X .
![]()
![]() 10.3.2. Доказать, что последовательность предыдущей задачи обрывается
(на пустом слове).
10.3.2. Доказать, что последовательность предыдущей задачи обрывается
(на пустом слове).
![]() 10.3.3. Доказать, что любое слово, одновременно являющееся началом
и концом слова X (кроме самого X ) входит в последовательность
10.3.3. Доказать, что любое слово, одновременно являющееся началом
и концом слова X (кроме самого X ) входит в последовательность
![]()