 3.2.1. Использовать метод обхода дерева для решения следующей
задачи: дан массив из n целых положительных чисел
3.2.1. Использовать метод обхода дерева для решения следующей
задачи: дан массив из n целых положительных чисел
![${\hbox{\tt a[1]}}\ldots{\hbox{\tt a[n]}}$](img147.gif) и число s; требуется узнать, может ли
число s быть представлено как сумма некоторых из чисел массива
a. (Каждое число можно использовать не более чем по одному
разу.)
и число s; требуется узнать, может ли
число s быть представлено как сумма некоторых из чисел массива
a. (Каждое число можно использовать не более чем по одному
разу.)
Решение. Будем задавать k-позицию последовательностью из
k булевских значений, определяющих, входят ли в сумму числа
![${\hbox{\tt a[1]}}\ldots{\hbox{\tt a[k]}}$](img228.gif) или не входят. Позиция допустима, если
ее сумма не превосходит s.
или не входят. Позиция допустима, если
ее сумма не превосходит s.
Замечание. По сравнению с полным перебором всех
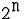 подмножеств тут есть некоторый выигрыш. Можно
также предварительно отсортировать массив a в убывающем
порядке, а также считать недопустимыми те позиции, в которых
сумма отброшенных членов больше, чем разность суммы всех членов
и s. Последний прием называют << методом ветвей и
границ>>. Но принципиального улучшения по сравнению с полным
перебором тут не получается (эта задача, как говорят,
NP -полна, подробности см. в книге Ахо,
Хопкрофта
и Ульмана
<< Построение и анализ вычислительных алгоритмов>>,
Мир, 1979,
а также в книге Гэри
и Джонсона
<< Вычислительные
машины и труднорешаемые задачи>>, Мир, 1982).
Традиционное
название этой задачи -- << задача о рюкзаке>> (рюкзак общей
грузоподъемностью s нужно упаковать под завязку, располагая
предметами веса
подмножеств тут есть некоторый выигрыш. Можно
также предварительно отсортировать массив a в убывающем
порядке, а также считать недопустимыми те позиции, в которых
сумма отброшенных членов больше, чем разность суммы всех членов
и s. Последний прием называют << методом ветвей и
границ>>. Но принципиального улучшения по сравнению с полным
перебором тут не получается (эта задача, как говорят,
NP -полна, подробности см. в книге Ахо,
Хопкрофта
и Ульмана
<< Построение и анализ вычислительных алгоритмов>>,
Мир, 1979,
а также в книге Гэри
и Джонсона
<< Вычислительные
машины и труднорешаемые задачи>>, Мир, 1982).
Традиционное
название этой задачи -- << задача о рюкзаке>> (рюкзак общей
грузоподъемностью s нужно упаковать под завязку, располагая
предметами веса ![${\hbox{\tt a[1]}}\ldots{\hbox{\tt a[n]}}$](img147.gif) ). См. также в главе
8 алгоритм ее решения, полиномиальный по
). См. также в главе
8 алгоритм ее решения, полиномиальный по
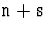 (использующий << динамическое
программирование>>).
(использующий << динамическое
программирование>>).
 3.2.2. Перечислить все последовательности из n нулей, единиц и
двоек, в которых никакая группа цифр не повторяется два раза
подряд (нет куска вида XX ).
3.2.2. Перечислить все последовательности из n нулей, единиц и
двоек, в которых никакая группа цифр не повторяется два раза
подряд (нет куска вида XX ).
 3.2.3. Аналогичная задача для последовательностей нулей и
единиц, в которых никакая группа цифр не повторяется три раза
подряд (нет куска вида XXX ).
3.2.3. Аналогичная задача для последовательностей нулей и
единиц, в которых никакая группа цифр не повторяется три раза
подряд (нет куска вида XXX ).
К этой же категории относятся задачи типа << можно ли
сложить данную фигуру из пентамино>> и им подобные. В них
важно умелое сокращение перебора (вовремя распознать, что
имеющееся расположение фигурок уже противоречит требованиям, и
по этой ветви поиск не продолжать).
pvv
1/8/1999
![]() 3.2.1. Использовать метод обхода дерева для решения следующей
задачи: дан массив из n целых положительных чисел
3.2.1. Использовать метод обхода дерева для решения следующей
задачи: дан массив из n целых положительных чисел
![]() и число s; требуется узнать, может ли
число s быть представлено как сумма некоторых из чисел массива
a. (Каждое число можно использовать не более чем по одному
разу.)
и число s; требуется узнать, может ли
число s быть представлено как сумма некоторых из чисел массива
a. (Каждое число можно использовать не более чем по одному
разу.)
![]() 3.2.2. Перечислить все последовательности из n нулей, единиц и
двоек, в которых никакая группа цифр не повторяется два раза
подряд (нет куска вида XX ).
3.2.2. Перечислить все последовательности из n нулей, единиц и
двоек, в которых никакая группа цифр не повторяется два раза
подряд (нет куска вида XX ).![]()
![]() 3.2.3. Аналогичная задача для последовательностей нулей и
единиц, в которых никакая группа цифр не повторяется три раза
подряд (нет куска вида XXX ).
3.2.3. Аналогичная задача для последовательностей нулей и
единиц, в которых никакая группа цифр не повторяется три раза
подряд (нет куска вида XXX ).![]()