• Урок 11. Решаем краевую задачу
• Пример с матрицей МКР
  • Формирование матрицы
• Метод прогонки
  • Разработка SDI-приложения
  • Класс окна для отображения графика
  • Класс графика
  • Конструктор С Graph
  • Преобразование координат
  • Отображение графика
  • Вспомогательная функция
  • Диалог для исследования решений

Решаем краевую задачу

• Пример с матрицей МКР
  
• Метод прогонки
  
• Разработка SDI-приложения
  
• Класс окна для отображения графика
  
• Класс графика
  
• Конструктор CGraph
  
• Диалог для исследования решений

В этом разделе мы разработаем MFC приложение с SDI-интерфейсом, которое использует контейнеры STL для хранения последовательностей величин, участвующих в формулировке простейшей одномерной краевой задачи матфизики. Сама задача формулируется в виде дифференциального уравнения, связывающего искомую функцию, пространственную координату и параметры, зависящие от свойств среды. Решение системы разностных уравнений, полученных путем аппроксимации дифференциального уравнения на сетке узлов, будет производиться методом прогонки. Контейнеры будут хранить дискретные значения коэффициентов уравнения и разностного аналога непрерывной функции.

Пример с матрицей МКР

Для начала рассмотрим пример использования valarray л его сечения в задаче, более близкой к жизни, чем все другие учебные примеры, приводившиеся ранее. Когда-то вы слышали о том, что электронные вычислительные машины (ЭВМ) изобрели для того, чтобы решать дифференциальные уравнения. Не удивлюсь, узнав, что существуют успешно зарабатывающие на жизнь программированием молодые люди, которые об этом не знают. Однако это правда. Рассмотрим npot стое уравнение, которое способно довольно сносно описать многие процессы и явления нашей жизни j

d/dx(p*(dU/dx))+kU=-f

Это уравнение Пуассона и оно, например, (при k = 0 и f = 0) способно описать стационарное тепловое поле в самом простом одномерном случае, когда температура U = U(x) почему-то зависит только от одной координаты х. Например, в длинном неоднородном стержне, теплоизолированном с боков. Символ р в этом случае имеет смысл коэффициента теплопроводности материала стержня, который в принципе может зависеть от координаты р = р(х), а символ f = f(x) имеет смысл точечного источника тепла. Если f тождественно равна нулю, то мы имеем частный случай — уравнение Лапласа. Источником теплового поля в этом случае является известная температура или скорость ее изменения на границах расчетной области. Отсюда происходит термин краевая задача, то есть задача, в которой заданы граничные условия (условия на краях расчетной области). В задачах такого рода требуется найти все значения температуры внутри области. Областью расчета в одномерном случае является отрезок прямой линии. Например, слева жарко, а справа холодно. Спрашивается, а как распределена температура внутри отрезка?

Считается, что в макромире температура распределена непрерывно, то есть в каждой точке, число которых не поддается счету, она имеет свое собственное значение. При попытке решить задачу на компьютере (сугубо дискретной структуре) надо отказаться от идеи бесконечности и ограничиться каким-то разумным числом точек, например N = 300. По опыту знаю, что график из трехсот точек вполне прилично выглядит на экране. Приняв это решение, разбивают всю область 300 точками на 299 отрезков и заменяют (аппроксимируют) производные дифференциального уравнения конечными разностями. Такова основная идея метода конечных разностей (МКР). При этом одно дифференциальное уравнение заменяется 298 алгебраическими уравнениями по числу внутренних точек, так как две граничные точки не требуют аппроксимации. Вот мы и пришли к необходимости решать систему алгебраических уравнений из 298 уравнений с 298 неизвестными температурами во внутренних точках расчетной области.

Точно такое же уравнение описывает и многие другие физические явления. Изменяется лишь смысл параметров р и k. Например, магнитное поле в центральном поперечном сечении электрической машины с некоторыми незначительными поправками, вызванными переходом к цилиндрической системе координат, тоже с успехом может быть описано подобным уравнением.

Для того чтобы поместить матрицу системы алгебраических уравнений в последовательность типа valarray и начать орудовать его сечениями (slice), надо сначала немного потрудиться и хотя бы понять структуру матрицы. Затем следует выработать алгоритм вычисления ее коэффициентов, и только после этого использовать динамические структуры данных и алгоритмы STL для решения задачи.

Тем, кто почувствовал себя неуютно в незнакомой обстановке, скажем, что это нетрудно и даже интересно. Поэтому не торопитесь отбросить книгу, а продолжайте чтение и, может быть, вы еще завоюете мир, разработав великолепный инструмент для решения краевых задач в трехмерной постановке. Для начала рассмотрите схему расчетной области, которая приведена на рис. 11.1.

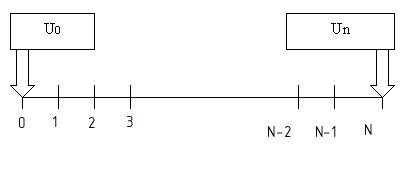
Рис. 11.1. Схема расчетных узлов по методу МКР

Напомним, что нашей задачей является найти значения температуры или любой другой функции U во всем множестве точек М = {1, 2, ..., N-2, N-1}, считая, что в двух точках {О, N} она известна. Переход к конечным разностям производится с помощью трехточечного шаблона, который изображен на рис. 11.2.

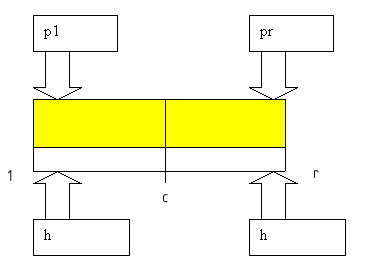
Рис. 11.2. Трехточечный шаблон аппроксимации второй производной

Мы имеем три точки и два отрезка, которых вполне достаточно, чтобы справиться со второй производной при попытке ее приближенного вычисления. Индексы 1, г и с означают left, right и center. Обозначение pi принято для коэффициента, учитывающего свойства среды левого отрезка, например теплопроводности, а рг — правого. Шаги разбиения области вдоль оси х считаются одинаковыми и равными h. Теперь вы должны представить себе, что центр этого шаблона по очереди приставляется ко всем точкам из множества М. В результате этой процедуры мы по одному будем получать все |М| = N - 1 алгебраических уравнений, приближенно заменяющих одно дифференциальное уравнение Пуассона, которое, как говорят физики, удовлетворяется во всех точках этой части реального пространства.

Возвращаясь к шаблону из трех точек, напомним, что производная по х — это в некотором роде степень изменения функции, то есть скорость ее роста или падения вдоль этой координаты. Приближенно она равна:

dU/dx=(Ur-Uc)/h

для правого отрезка и

dU/dx=(Uc-Ul)/h

для левого. Теперь надо записать приближенную оценку для второй производной с учетом коэффициента теплопроводности. Он может иметь разные значения (р! и рг) в левой и в правой частях шаблона:

d/dx(pdU/dx)={(pr[Ur-Uc])/h-(pl[Uc-Ul])/h}/h (2)

Произведя подстановку в исходное дифференциальное уравнение (1) и упростив выражение, получим алгебраическое уравнение:

aUl+bUc+cUr=0 (3)

связывающее температуры трех соседних узлов сетки с физическими свойствами прилежащих участков пространства, так как значения коэффициентов уравнения зависят от р, k и h:

a=pl/h^2; c=pr/h^2; b=-a-c+k; (4)

Коэффициент а описывает свойства левой части шаблона, а с — правой, а Ь — обеих вместе. Чуть позже мы увидим, что коэффициент b попадет в диагональ матрицы. Теперь надо примерить шаблон ко всем узлам сетки. Узел номер 1 даст уравнение:

a1U0+b1U1+c1U2=0,

узел номер 2:

a2U1+b2U2+c2U3=0,

и т. д. Здесь важно следить за индексами. Для простоты пока считаем, что коэффициенты а,, b,, с, не изменяются при переходе от узла к узлу. В узлах сетки вблизи границ (то есть в узле 1 и узле N-1) уравнения упрощаются, так как £/„ и U_N считаются известными и поэтому перемещаются в правую часть уравнения. Так, первое уравнение системы станет:

b1U1+c1U2=0,

а последнее:

an-1Un-2+bn-1Un=+1=0,

Все остальные уравнения будут иметь вид (3). Теперь пора изобразить всю систему уравнений, используя матричные обозначения и не отображая многочисленные нули. Для простоты будем считать, что N = 5:

Вы видите, что матрица системы уравнений имеет характерную регулярную трех-диагональную структуру, а структура вектора правых частей тоже легко прочитывается. Граничные; условия краевой задачи заняли подобающие им крайние места, а внутренние позиции — нули.

Решать такую систему следует специальным методом, который называется методом прогонки и является модификацией метода Гаусса. Он работает во много раз быстрее самого метода Гаусса. Мы реализуем его немного позже, а сейчас попробуем применить алгоритм generate из библиотеки STL для генерации матрицы, имеющей рассмотренную структуру, и вектора решений U. В простых случаях он известен и легко угадывается. Затем с помощью сечений произведем умножение Матрицы на вектор и убедимся в том, что вектор правых частей системы уравнений будет иметь правильную структуру и значения. Эту часть работы рассматривайте как дополнительное упражнение по использованию структур данных типа valarray и slice. В процессе решения краевой задачи мы будем пользоваться контейнерами другого типа (vector), так как метод прогонки не требует применения каких-то особых приемов работы с сечениями.

Если для простоты принять р = 1, h = 1, U₀ = 100, a U_N =0, то коэффициенты матрицы будут равны a_i = с_i = 1, b_i. = -2 , k = 0, а решение U(x) известно заранее. Это — линейно спадающая от 100 до 0 функция, а в более общем случае — функция произвольных граничных условий:

U(x)=U0+[Un-U0]x/L

где L — длина всей расчетной области. Правильность решения проверяется прямой подстановкой в уравнение (1).

Формирование матрицы

Учитывая сказанное, создадим программный модуль, который позволяет проверить наши возможности управления последовательностью valarray на примере задачи, близкой к реальности. Самым сложным моментом в реализуемом плане является создание функции f (), с помощью которой генерируется матрица заданной структуры, но произвольной размерности п. При генерации она помещается в последовательность типа valarray. Вторая функция (f и) проста. С ее помощью вычисляются коэффициенты уже известного вектора решений¹:

//====== Глобально заданная размерность системы

int n;

//====== Граничные условия

double UO, UN;

//====== Функция вычисления коэффициентов

//====== трехдиагональной матрицы

double f ()

{

//====== Разовые начальные установки

static int raw = -1, k = -1, col = 0;

//====== Сдвигаемся по столбцам

col++;

//====== k считает все элементы

//====== Если начинается новая строка

if (++k % n == 0)

{

col =0; // Обнуляем столбец

raw++; // Сдвигаемся по строкам

}

//====== Выделяем три диагонали

return col==raw ? -2.

: col == raw-1 И col==raw+l ? 1.

: 0.;

}

double fu()

{

//==== Вычисления вектора правых частей по формуле (5)

static double

dU = (UN-UO)/(n+1),

d = UO; return d += dU;

}

В функции main создается valarray с трехдиагональной матрицей и производится умножение матрицы на вектор решений. Алгоритм умножения использует сечение, которое вырезает из valarray текущую строку матрицы:

void main()

{

//======= Размерность задачи и граничные условия

n =4;

UO = 100.;

UN = 0 . ;

//======= Размерность valarray (вся матрица)

int nn = n*n;

//======= Матрица и два вектора

valarray<double> a(nn), u(n), v(n);

//======= Генерируем их значения

generate (&а[0], &a[nn], f); generate (&u[0], &u[n], fu);

out ("Initial matrix", a); out ("Initial vector", u);

//======= Умножение матрицы на вектор

for (int i=0; i<n; i++) {

//======= Выбираем i-ю строку матрицы

valarray<double> s = a[slice (i*n, n , 1)];

//======= Умножаем на вектор решений

//======= Ответ помещаем в вектор v <

transform(&s[0], &s[n], &u[0], &v[0], multiplies<double>());

//======= Суммируем вектор, получая

//======= i-ый компонент вектора правых частей

cout « "\nb[" « i « "] = " « v.sum(); }

cout«"\n\n";

}

Так как мы знаем структуру вектора правых частей, то, изменяя граничные условия и порядок системы, можем проверить достигнутую технику работы с сечениями.

Тестирование обнаруживает появление численных погрешностей (в пределах Ю"¹⁵), обусловленных ограниченностью разрядной сетки, в случаях когда диапазон изменения искомой величины не кратен размеру расчетной области. Стоит отметить, что сечения хоть и являются непривычным инструментом, для которого хочется найти наилучшее применение, но в рамках нашей задачи вполне можно обойтись и без него. Например, алгоритм умножения матрицы на вектор можно выполнить таким образом:

for (int i=0, id=0; i<n; i++, id+*n)

{

transform(&a[id], &a[id+n], &u[0], &v[0],

multiplies<dovible> () ) ;

cout « "\nb[" « i « "] = " « v.sum();

}

Эффективность этой реализации, несомненно, выше, так как здесь на один valarray меньше. Я думаю, что вы, дорогой читатель, сами найдете достойное применение сечениям.

Метод прогонки

Прогонкой называется модификация метода Гаусса для решения систем линейных алгебраических уравнений с трехдиагональной матрицей. Если матрица системы обладает определенными свойствами, то метод прогонки является численно устойчивым и очень эффективным методом, который позволяет практически мгновенно решать одномерные краевые задачи, одну из которых мы рассмотрели в предыдущем разделе. Большинство корректно поставленных физических задач приводит к системе уравнений с хорошей матрицей, и в этих случаях метод прогонки проявляет слабую чувствительность как к погрешностям задания начальных условий, так и к погрешностям вычислительного характера.

В предыдущем разделе была сформулирована так называемая первая краевая задача, в которой требуется найти значения функции во внутренних узлах сетки при условии, что на границах области они известны. В теории и на практике рассматриваются задачи с более сложными граничными условиями. Например, когда на одной из границ известна не функция, а ее первая производная — граничное условие второго рода. Имеют место и постановки задач с граничными условиями третьего рода, когда на границе должно выполняться какое-то известное заранее соотношение между функцией и ее первой производной. С точки зрения численной реализации все три типа задач можно описать с помощью соотношений одного и того же вида:

U0=y0U1+б0, (6)

Un=ynUn-1+бn, (7)

Они связывают значения разностных аналогов Ui, непрерывной функции U(x) в двух узлах, прилегающих к левой или правой границе. Так, граничное условие первого рода и_Uo = с может быть задано с помощью пары параметров: у₀= 0, б0 = с, а условие второго рода dU/dx|0= с с помощью другой лары: у0 = 1,бo=ch, где h — это шаг сетки. В нашем приложении будет работать немодальный диалог, который позволит пользователю задавать различные типы граничных условий, изменяя численные значения четырех коэффициентов у_o, бo, yn, бn

Суть метода прогонки заключается в том, что, используя специфику структуры матрицы системы уравнений (наличие трех диагоналей), удается получить рекуррентные формулы для вычисления последовательности коэффициентов прогонки, которые позволяют на обратном ходу вычислить значения функции в узлах сетки. Рассматривая конечно-разностное уравнение для первой тройки узлов:

b1U1+c1U2=-a1U0,

видим, что оно совпадает по форме с обобщенным граничным условием (6) и связывает между собой два соседних значения U1, и U₂. Перепишем его в виде:

d1U2+e=U1, (8)

где d₁ и е1вычисляются по известным значениям. Наблюдательный читатель заметит, что это справедливо только для задач первого рода. Чуть позже мы получим общее решение. Теперь мы можем исключить £/, из уравнения для следующей тройки узлов:

a2U1+b2U2+c2U2=f2,

подставив значение U1 из уравнения (8). После этой процедуры последнее уравнение также может быть приведено к виду:

d3U3+e2=U2,

Подстановки можно продолжать и дальше, но для получения рекуррентного соотношения, достаточно рассмотреть одну из них для произвольного индекса i. Подставив

di-1Ui+ei-1=Ui-1,

в уравнение

aiUi-1+biUi+ciUi+1=fi,

получим:

Ui=-[CiUi+1/(aidi-1+bi)]+[fi-ai+1*ei+1/(aidi-1+bi)] (9)

Это соотношение дает две рекуррентные формулы для коэффициентов:

di=-Ci/(ai*di-1+bi) (10)

ei=(fi-ai*ei-1)/(aidi-1+bi) (11)

Цикл вычисления последовательности коэффициентов в соответствии с этими формулами носит название прямого хода прогонки. Начальные значения коэффициентов определяются предварительно заданным граничным условием (6):

do=yo, eo=бo,

Цикл прямого хода повторяется N-1 раз. Последними будут вычислены коэффициенты d_N-1 и e_N-1, которые связывают функции в двух узлах вблизи правой границы:

Un-1=dn-1Un+en-1 (12)

Если на правой границе задано условие первого рода U_n = с, то уже можно вычислить U_n-1 по формуле (12) и далее продолжать обратный ход прогонки, используя уравнения (9) при I = N - 1,..., 1, 0. Если условие более сложное, то вместе с уравнением (12) надо рассмотреть уравнение (7), определяющее граничное условие на правой границе. Напомним его:

Un=ynUn-1+бn (7)

Соотношения (7) и (12) составляют систему из двух уравнений с двумя неизвестными. Используя определители, запишем ее решение.

Un-1=(en-1+бndn-1)/(1-yndn-1) (13)

Un=(бn+ynen-1)/(1-yndn-1)

Таким образом, мы нашли значения в двух узлах, лежащих вблизи правой границы расчетной области. Теперь, используя формулу (9) и уменьшая индекс i от N= 2 до 0, можно вычислить все неизвестные £/.. Этот процесс носит название обратного хода прогонки. Почему-то в голову приходит лозунг нашего времени: «Цели ясны, задачи определены. За работу, товарищи!» Нам осталось всего лишь реализовать описанный алгоритм в виде MFC-приложения.

Разработка SDI-приложения

Создайте новый проект типа MFC Application и назовите его Heat, несмотря на то что наша задача немного переросла задачу расчета стационарного теплового поля.

1. При выборе типа приложения установите переключатель Select application type в положение Single Document и снимите для разнообразия флажок Document/View architecture support.
   
2. На странице User Interface Features установите флажок Maximized, с тем чтобы окно приложения при начальном запуске открывалось полностью.
3. На странице Advanced Features можно снять флажок ActiveX Controls.
   
4. Нажмите кнопку Finish.

Если вам хочется увидеть, как ведет себя заготовка подобного рода, то запустите приложение (Ctrl+F5) и убедитесь, что его возможности соответствуют стандарту SDI. Откройте файл StdAfx.h и вставьте сакраментальные коды подключения нужных библиотек:

#include <vector> using namespace std;

Класс окна для отображения графика

Откройте файл ChildView.cpp, который содержит коды реализации методов класса CChildView. Его имя содержит ложный намек на происхождение от CView. На самом деле он происходит от класса CWnd и инкапсулирует функциональность окна, оккупирующего клиентскую область окна рамки, которое управляется классом CMainFrame. Простое окно, как вы помните, для перерисовки своего содержимого, вместо метода OnDraw использует метод OnPaint. Найдите этот метод в классе CChildView и убедитесь, что в нем контекст устройства создается, а не приходит в качестве параметра от каркаса приложения, как это было в приложениях, поддерживающих архитектуру документ — представление. Вставьте внутрь этого метода вызов конструктора класса CGraph с последующим сообщением Draw:

void CChildView::OnPaint() {

CPaintDC dc(this);

CGraph(m_Points, "Field Distribution", "x[m]","Field").Draw(&dc); }

Класс CGraph разработаем позже. Он будет создавать двухмерный график функции — решения краевой задачи, автоматически масштабируемый и подстраивающийся под текущий размер окна CChildView. Перейдите к файлу с определением оконного класса (ChildFrame.h) и введите следующие коррективы:

# pragma once

#include "Graph.h"

Class CChildView : public CWnd

{

// Вспомогательные классы будут пользоваться данными

friend class CParamDlg;

friend class CGraph;

private:

//===== Контейнер координат точек графика

vector<CDPoint> m_Points;

//===== Вектор источников и свойств среды (см. f и р)

vector<double> m_f, m_r;

//===== Размерность задачи (см. N)

int m_n;

//===== Параметры

double m_k, // Коэффициент k

m_L, // Протяженность расчетной области

m_g0, // Коэффициенты, задающие ГУ слева

m_d0,

m_gn, // Коэффициенты, задающие ГУ справа m_dn ;

CParamDlg *m_pDlg; // Немодальный диалог параметров

public:

CChildView();

virtual -CChildViewO;

virtual BOOL PreCreateWindow(CREATESTRUCT& cs);

//===== Изменение размерности задачи

void Resize();

//===== Решение системы методом прогонки

void Solve();

protected:

afx_msg void OnPaintO;

DECLARE_MESSAGE_MAP() };

Точки графика будем хранить в контейнере объектов класса CDPoint, который мы неоднократно использовали, так как исследователи реальных систем работают с вещественными координатами. Переход к экранным координатам будет произведен в классе CGraph. Инициализацию данных проведите в конструкторе оконного класса:

CChildView: :CChildView()

{

m_n = 200;

m_k = -0.0005;

m_L = 200.;

//====== Слева ГУ первого рода Uo=100

m_g0 = 0.;

m_d0 =100.;

m_gn = 0.;

m_dn = 0.;

Resize () ;

m_pDlg = 0;

}

В деструктор вставьте коды освобождения памяти, занимаемой контейнерами:

CChildView::~CChildView()

{

m_Points.clear();

m_f.clear();

m_r.clear();

}

При работе с диалогом по управлению параметрами пользователь будет иметь возможность изменять количество узлов разбиения расчетной области, поэтому мы должны изменять размерность используемых контейнеров:

void CChildView::Resize ()

{

//===== Число узлов равно N+1 (с учетом 0-го узла)

int n = m n + 1;

m_Points.resize(n, CDPoint(0.,0.));

m_f.resize(n, 0.);

m_r.resize(n, 1.); }

Функция Solve решает систему уравнений методом прогонки:

void CChildView::Solve()

{

Resize () ;

int n = m_n + 1;

//======= Коэффициенты разностных уравнений

vector<double> a(n), b(n), c(n);

//======= Коэффициенты прогонки

vector<double> d(n), e(n);

double h = m L / m_n, // Размер шага вдоль оси х

hh = h * h;

// Квадрат шага

//======= Коэффициенты с 0-м индексом не используются

а[0] = 0.;

b[0] = 0.;

с[0] = 0.;

//=== Вычисляем координаты х и коэффициенты уравнений

m_Points[0].х = 0.;

for (int i=1; i < m_n; i++)

{

m_Points[i],x = i * h;

//======= Смотри формулы (4)

a[i] = m_r[i-l]/hh;

c[i] = m_r[i]/hh;

b[i] = - a[i] - c[i] + m_k;

}

m_Points[m_n].x = m_L;

//======== -Прямой ходпрогонки

d[0] = m_gO; //ГУ слева e[0] * m_d0; double den;

for (i=1; i < m_n; 1++)

{

//======= Общий знаменатель

den = a[i) * d[i-l] + b[i] ; d[i] = -c[i] / den;

e[i] = <m_f[i] - a[i] * e[i-l]) / den;

}

//======= Готовимся к обратному ходу

den = 1. - m_gn * d[m_n-l];

//======= Случай некорректно поставленной задачи

if (den==0.)

{

MessageBox ("ГУ заданы некорректно", "Ошибка-",МВ_ОК) ;

return;

}

//====== Два последних узла используют ГУ справа

//======= Смотри формулы (13)

m_Points[m_n-l].у = (e[m_n-l] + m_dn * d[m_n-l])/den;

m_Points[m_n].y = (m_dn + m_gn* e[m_n-l])/den;

//======= Обратный ход прогонки

for (i = m_n-2; i >= 0; i--)

m_Points[i].y = d[i) * m_Points[i+1].у + e[i]; Invalidate();

}

С помощью инструментов Studio.Net введите в класс CChildView реакцию на сообщение о создании окна WM_CREATE и вставьте в нее единственную строку, которая вызывает функцию Solve. Она формирует и решает систему разностных уравнений, определенную данными по умолчанию. Позже мы создадим диалог по изменению этих данных:

int CChildView::OnCreate(LPCREATESTRUCT IpCreateStruct)

{

if (CWnd::OnCreate(IpCreateStruct) == -1)

return -1;

//======= Решаем систему, определенную по умолчанию

Solved;

return 0;

}

Класс графика

С помощью Studio.Net введите в состав проекта новый generic-класс CGraph, не указывая имени базового класса и не включая флажок Virtual destructor. В файл декларации нового класса введите вручную вспомогательный класс CDPoint, необходимость в котором мы обсуждали ранее. Затем добавьте объявление структуры TData, которая собирает воедино все данные, используемые при построении графика. Начальная буква Т в имени класса осталась со времен работы в среде Borland. Там принято все классы именовать начиная с буквы Т (Туре), означающей создание нового типа данных. Но в отличие от старой реализации графика, которая, возможно, знакома читателю по книге «Технологии программирования на языке C++» (Издательство СПбГТУ, 1997), мы введем в класс CGraph некоторые новые возможности:

#pragma once

class CDPoint

{

public:

//=== Две вещественные координаты точки на плоскости

double x, у;

//======= Стандартный набор конструкторов и операций

CDPoint () {

х=0.; у=0.;

}

CDPoint(double xx, double yy) {

х=хх;

У=УУ;

}

CDPoints operator=(const CDPointi pt) {

x = pt.x;

У = pt.y; return *this;

}

CDPoint(const CDPointS pt) {

*this - pt; } };

//===== Вспомогательные данные, характеризующие

//== последовательность координат вдоль одной из осей

struct TData (

//===== Порядок в нормализованном представлении числа

int Power; //===== Флаг оси X

bool bХ; double

//======= Экстремумы

Min, Max,

//======= Множитель -(10 в степени Power)

_{

Factor,

//======= Шаг вдоль оси (мантисса)

Step,

//======= Реальный шаг

dStep,

//==== Первая и последняя координаты (мантиссы)

Start, End,

// ======= Первая и последняя координаты

dStart, dEnd; };

//===== Класс, реализующий функции плоского графика

class CGraph { public:

//===== Данные, характеризующие данные вдоль осей

TData m_DataX, m_DataY;

//===== Контейнер точек графика

vector <CDPoint>& m_Points;

//===== Текущие размеры окна графика

CSize m_Size;

//===== Экранные координаты центра окна

CPoint m_Center;

//===== Заголовок и наименования осей

CString m_sTitle, m_sX, m_sY;

//===== Перо для рисования

CPen m_Pen;

//===== Два типа шрифтов

CFont m_TitleFont, m_Font;

//===== Высота буквы (зависит от шрифта)

int m_LH,

//===== Толщина пера

m_Width;

//===== Цвет пера COLORREF m_Clr;

//======= Методы для управления графиком

CGraph(vector<CDPoint>& pt, CString sTitle, CString sX, CString sY) ;

virtual -CGraph();

//===== Заполнение TData для любой из осей

void Scale(TDataS data);

//===== Переход к логическим координатам точек

int MapToLogX (double d);

int MapToLogY (double d);

//===== Изображение в заданном контексте

void Draw (CDC *pDC);

//===== Изображение одной линии

void DrawLine(CDC *pDC) ;

//===== Подготовка цифровой метки на оси

CString MakeLabel(bool bx, doubles d);

};

Класс CGraph сделан с учетом возможности развития его функциональности, так чтобы вы могли добавить в него нечто и он мог бы справиться с несколькими кривыми одновременно. Фактически он представляет собой упрощенную версию того класса, которым мы пользуемся для отображения результатов расчета поля в двухмерной постановке. Отметьте, что структура TData используется как для последовательности абсцисс, так и ординат.

Алгоритм нормирования абсцисс и ординат проще создать, чем кратко и понятно описать. Тем не менее попробуем дать ключ к тому, что происходит. Мы хотим, чтобы размеры графика отслеживали размеры окна, а числа, используемые для разметки осей, из любого разумного диапазона, как можно дольше оставались читабельными. Задача трудновыполнимая, если динамически не изменять шрифт. В данной реализации мы не будем подбирать, а используем только два фиксированных шрифта: для оцифровки осей и для вывода заголовка графика. Обычно при построении графиков числа, используемые для оцифровки осей (мантиссы), укладываются в некоторый разумный диапазон и принадлежат множеству чисел, кратных по модулю 10, стандартным значениям шага мантиссы (2, 2.5, 5 и 10). Операцию выбора шага сетки, удовлетворяющую этим условиям, удобно выполнить в глобально определенной функции, не принадлежащей классу CGraph. Это дает возможность использовать функцию для нужд других алгоритмов и классов. Ниже приведена функция gScale, которая выполняет подбор шага сетки. Мы постепенно дадим содержимое всего файла Graph.срр, поэтому вы можете полностью убрать существующие коды заготовки. Начало файла имеет такой вид:

#include"StdAfx.h"

#include "graph.h"

//===== Доля окна, занимаемая графиком

#define SCAT,F,_X 0 . 6

#define SCALE_Y 0.6

//=== Внешняя функция нормировки мантисс шагов сетки

void gScale (double span, doubles step)

{

//== Переменная span определяет диапазон изменения

//== значаний одной из координат точек графика

//== Вычисляем порядок числа, описывающего диапазон

int power = int(floor(loglO(span)));

//===== Множитель (zoom factor)

double factor = pow(10, power);

//===== Мантисса диапазона (теперь 1 < span < 10)

span /= factor;

//===== Выбираем стандартный шаг сетки if (span<1.99)

step=.2;

else if (span<2.49)

step=.25;

else if (span<4.99)

step=.5;

else if (span<10.)

step= 1.;

//===== Возвращаем реальный шаг сетки (step*10~power)

step *= factor;

}

Результатом работы функции gScale является значение мантиссы дискретного шага сетки, которая наносится на график и оцифровывает оду из осей. Самым сложным местом в алгоритме разметки осей является метод CGraph:: Scale. Он по очереди работает для обеих осей и поэтому использует параметр с данными типа TData, описывающими конкретную ось. Особенностью алгоритма является реализация идеи, принадлежащей доценту СПбГТУ Александру Калимову и заключающейся в том, чтобы как можно дольше не переходить к экспоненциальной форме записи чисел. Обычно Калимов использует форму с фиксированной запятой в диапазоне 7 порядков изменения чисел (10~³+10⁴), и это дает максимально удобный для восприятия формат, повышая читабельность графика:

void CGraph::Scale (TDatai data)

{

//===== С пустой последовательностью не работаем

if (m_Points.empty()) return;

//===== Готовимся искать экстремумы

data.Max = data.bX ? m_Points [0] .х : m_Points [0] .у;

data.Min = data.Max;

//===== Поиск экстремумов

for (UINT j=0; j<ra_Point5.size(); j++)

{

double d = data.bX ?

m_Points [ j] .x

: m_Points [ j] . y;

if (d < data.Min) data.Min = d;

if (d > data.Max) data.Max = d;

}

//===== Максимальная амплитуда двух экстремумов

double ext = max(fabs(data.Min),fabs(data.Max));

//===== Искусственно увеличиваем порядок экстремума

//===== на 3 единицы, так как мы хотим покрыть 7 порядков,

//===== не переходя к экспоненцеальной форме чисел

double power = ext > 0.? loglO(ext) +3. : 0.;

data.Power = int(floor(power/7.));

//===== Если число не укладывается в этот диапазон

if (data.Power != 0)

//===== то мы восстанавливаем значение порядка

data.Power = int(floor(power)) - 3;

//===== Реальный множитель

data.Factor = pow(10,data.Power);

//===== Диапазон изменения мантиссы

double span = (data.Max - data.Min)/data.Factor;

//===== Если он нулевой, if (span == 0.)

span = 0.5; // то искусственно раздвигаем график

// Подбираем стандартный шаг для координатной сетки

gScale (span, data.Step);

//===== Шаг с учетом искусственных преобразований

data.dStep = data.Step * data.Factor;

//== Начальная линия сетки должна быть кратна шагу

//====и быть меньше минимума

data.dStart = data.dStep *

int (floor(data.Min/data.dStep));

data.Start = data.dStart/data.Factor;

//===== Вычисляем последнюю линию сетки

for (data.End = data.Start;

data.End < data.Min/data.Factor + span-le-10;

data.End += data.Step)

data.dEnd = data.End*data.Factor;

}

Конструктор CGraph

Если вы поняли, что происходит в методе Scale, то дальнейшие манипуляции с данными графика не вызовут у вас затруднений. Рассмотрим конструктор класса CGraph. В первом параметре по ссылке он получает контейнер с точками графика. Для того чтобы исключить копирование всех точек внешнего контейнера, мы инициализируем в заголовке конструктора свою собственную ссылку m_Points на входной контейнер. Кроме контейнера с точками графика пользователь объектом CGraph должен передать два текста, помечающих оси графика (sX, SY) и текст его заголовка (sTitle). В теле конструктора готовим два объекта типа TData для данных о разметке двух осей, создаем два шрифтовых объекта и инициализируем переменные управления параметрами линии графика. В данной реализации мы убрали диалог по изменению атрибутов пера, который вы можете сделать по своему вкусу.

Следует отметить, что при изображении нескольких кривых функциональных зависимостей на одном графике необходимо дать пользователю возможность управлять стилем пера для каждой кривой в отдельности. В начале книги мы рассматривали, как это делается. Кроме того, следует учитывать существующие традиции изображения научной графики. Например, можно помечать кривые крестиками, ноликами и т. д. Это делается с помощью цикла прохода по точкам кривой и вывода в определенных местах растровых изображений, маркирующих кривую. Эти возможности ввиду необходимости описывать объекты классов Stingray Objective Grid мы также убрали из данной реализации.

//======= Конструктор класса CGraph

CGraph::CGraph (vector<CDPoint>S pt,

CString sTitle, CString sX, CString sY)

: m_Points(pt)

{

//===== Готовим данные, характеризующие оси координат

ZeroMemory(Sra_DataX, sizeof(TData));

ZeroMemory(sm_DataY, sizeof(TData));

m_DataX.bX = true;

m_DataY.bX = false;

m_sTitle = sTitle;

m_sX = sX;

m_sY = sY;

//======= Создаем шрифт для оцифровки осей

m_Font.CreateFont(16,0,0,0,100,0,0,0,DEFAULT_CHARSET,

OUT_RASTER_PRECIS,CLIP_DEFAULT_PRECIS,

DEFAULT_QUALITY,FF_DONTCARE,"Arial");

//======= Выясняем вертикальный размер буквы

TEXTMETRIC tm; CClientDC dc(0);

dc.SelectObject(Sm_Font);

dc.GetTextMetrics(Stm);

m_LH = tm.tmHeight;

//======= Создаем шрифт для вывода заголовка

m_TitleFont.CreateFont(24,О,О,0,100, 0, 0, 0,

DEFAULT_CHARSET, OUT_RASTER__PRECIS,

CLIP_DEFAULT_PRECIS, DEFAULT_QUALITY, FF_DONTCARE,

"Times New Roman");

//======= Задаем параметры пера

m_Clr = RGB(О,О,255); m_Width = 2;

}

Преобразование координат

В контейнере точек графика, на который ссылается переменная m_Points, хранятся мировые координаты, то есть числа, заданные в тех единицах измерения, которыми пользуется исследователь, решающий дифференциальное уравнение. Это удобно с той точки зрения, что пользователь видит и редактирует величины, к которым он привык. Для изображения графика на экране следует преобразовать мировые координаты в логические, с которыми работает подсистема GDI. На этот раз мы не будем пользоваться услугами Windows для преобразования логических координат в физические. А используем тот факт, что в режиме преобразования MMJTEXT, принятом по умолчанию, логические координаты соответствуют оконным, физическим. Мы сами будем нормировать координаты точек графика, загоняя их в диапазон (-0.5... 0.5), отслеживать изменения в размерах окна и пропорционально изменять размеры графика. По умолчанию у нас выбраны пропорции 0.6 х 0.6, что означает, размеры графика будут составлять 0.6 от размеров клиентской области окна. Преобразование координат производят два метода MapToLogX и MapToLogY. Каждый из них получает нормированную координату, а возвращает оконную. Изображение центрируется в окне с помощью переменной cpoint m_Center, значение которой должно корректироваться при каждой перерисовке. Размеры изображения зависят от текущих размеров окна (переменная csize m_size;), которые также вычисляются при каждой перерисовке:

int CGraph::MapToLogX (double d)

{

return m_Center.x + int (SCALE_X * m_Size.cx * d); }

int CGraph::MapToLogY (double d)

{

return m_Center.y - int (SCALE_Y * m_Size.cy * d); }

//======= Деструктор

CGraph::-CGraph(){}

Деструктор не производит никаких действий, так как в классе CGraph мы не используем динамических типов данных. Контейнер точек m_Points является всего лишь ссылкой на одноименный контейнер, который хранится в классе CChildView. Там же и происходит освобождение его памяти.

Отображение графика

График отображается в такой последовательности. Сначала рисуется ограничивающий прямоугольник (рамка), затем дважды вызывается функция Scale, которая подготавливает данные для разметки осей. После этого выводятся экстремальные значения функции. В этот момент в более сложном случае следует создавать и выводить так называемую легенду графика — информацию о соответствии маркеров и стилей линий определенным кривым. Так как мы изображаем только одну кривую, то эта часть работы сведена к минимуму. Перед тем как отобразить координатную сетку, следует создать и выбрать в контекст другое перо (gridPen). Сама сетка изображается в двух последовательных циклах прохода по диапазонам координат, подготовленных в методе Scale.

В каждом цикле мы сначала нормируем текущую координату, затем преобразовываем ее в оконную, вызывая одну из функций типа MapToLog*. Одновременно с линией сетки выводится цифровая метка. В ходе процесса нам несколько раз приходится менять способ выравнивания текста (см. вызовы SetTextAlign). Подстройка местоположения текста осуществляется с помощью переменной m_LH (better Height), значение которой зависит от выбранного размера шрифта. После вывода координатной сетки происходит вывод трех строк текста: метки осей и заголовок графика. В последнюю очередь происходит вывод самой кривой графика. В более сложном случае, который не реализован, мы в цикле проходим по всем объектам класса MyLine и просим каждую линию изобразить себя в нашем контексте устройства. Каждая линия при этом помнит и использует свой стиль, толщину, цвет и маркировку:

void CGraph::Draw(CDC *pDC) {

//====== С помощью контекста устройства

//====== узнаем адрес окна, его использующего

CWnd *pWnd =pDC->GetWindow();

CRect r;

pWnd->GetClientRect(ir);

//====== Уточняем размеры окна

m_Size = r.Size();

m_Center = CPoint(m_Size.cx/2, m_Size.cy/2);

//====== Сохраняем атрибуты контекста

int nDC = pDC->SaveDC();

//====== Создаем черное перо для изображения рамки

CPen pen(PS_SOLID, О, COLORREF(0));

pDC->SelectObject(Spen);

//====== Преобразуем координаты рамки

int It = MapToLogX(-0.S),

rt = MapToLogX(0.S),

tp = MapToLogY(0.S),

bm = MapToLogY(-0.S);

pDC->Rectangle (It, tp, rt, bm);

//====== Задаем цвет и выравнивание текста

pDC->SetTextColor (0);

pDC->SetTextAlign(TA_LEFT | TA_BASELINE);

//====== Выбираем шрифт

pDC->SelectObject (&m_Font);

//====== Вычисляем атрибуты координатных осей

Scale(m_DataX); Scale(m_DataY);

//====== Выводим экстремумы функции

CString s;

s.Format("Min = %.3g",m_DataY.Min);

pDC->TextOut(rt+m_LH, tp+m_LH, s) ;

s.Format("Max = %.3g",m_DataY.Max);

pDC->TextOut(rt+m_LH, tp+m_LH+m_LH, s);

//====== Готовимся изображать координатную сетку

CPen gridPen(PS_SOLID, 0, RGB(92,200, 178));

pDC->SelectObject(SgridPen);

pDC->SetTextAlign(TA_CENTER | TA_BASELINE);

//======Рисуем вертикальные линии сетки

for (double x = m_DataX.Start;

X < m_DataX.End - m_DataX.Step/2.;

x += m_DataX.Step) {

//====== Нормируем координату х

double xn = (x - m_DataX.Start) /

(m_DataX.End - m_DataX.Start) - 0.5;

//====== Вычисляем оконную координату

int xi = MapToLogX(xn);

//====== Пропускаем крайние линии,

//====== так как они совпатают с рамкой

if (x > m_DataX.Start && x < m_DataX.End)

{

pDC->MoveTo(xi, bm);

pDC->LineTo(xi, tp); )

//====== Наносим цифровую метку

pDC->TextOut (xi, bm+m_LH, MakeLabel(true, x)); }

//=== Повторяем цикл для горизонтальных линий сетки

pDC->SetTextAlign(ТА RIGHT | TA_BASELINE);

for (double у = m_DataY.Start;

у < m_DataY.End - m_DataY.Step/2.; у += m_DataY.Step)

{

double yn = (y - m_DataY.Start) /

(m_DataY.End - m_DataY.Start) - 0.5;

int yi = MapToLogY(yn);

if (y > m_DataY. Start &S, у < m_DataY.End)

{

pDC->MoveTo(lt, yi) ;

pDC->LineTo(rt, yi) ;

pDC->TextOut(lt-m_LH/2,yi,MakeLabel(false, y));

}

}

//====== Вывод меток осей

pDC->TextOut(lt-m_LH/2, tp - m_LH, m_sY);

pDC->SetTextAlign(TA_LEFT | TA_BASELINE);

pDC->TextOut(rt-m_LH, bm + m_LH, m_sX);

//====== Вывод заголовка

if (ra_sTitle.GetLength() > 40)

m_sTitle.Left(40);

pDC->SelectObject(Sm_TitleFont);

pDC->SetTextAlign(TA_CENTER | TA_BASELINE);

pDC->TextOut((It+rt)/2, tp - m_LH, m_sTitle);

//====== Вывод линии графика

DrawLine(pDC);

//====== Восстанавливаем инструменты GDI

pDC->RestoreDC(nDC);

}

Вывод линии графика начинается с создания и выбора пера. Эти действия можно вынести и поместить в какой-нибудь диалог по изменению атрибутов пера, но мы не будем этого делать, так как данное действие целесообразно только в случае, когда график состоит из нескольких линий. Обе координаты каждой точки сначала нормируются переходом к относительным значениям в диапазоне (-0.5*0.5), затем приводятся к оконным. После чего точки графика последовательно соединяются с помощью GDI-функции LineTo:

void CGraph::DrawLine(CDC *pDC) {

//====== Уничтожаем старое перо

if (m_Pen.m_hObject)

m_Pen.DeleteObject() ; //====== Создаем новое

m_Pen.CreatePen(PS_SOLID, m_Width, m_Clr);

pDC->SelectObject(im_Pen);

double x0 = m_DataX.dStart,

y0 = m_DataY.dStart,

dx = m_DataX.dEnd - x0,

dy = m_DataY.dEnd - y0;

//====== Проход по всем точкам

for (UINT i=0; i < m_Points.size(); i++) {

//====== Нормируем координаты

double x = (ra_Points[i].x - xO) / dx - .5,

у = (m_Points[i].у - y0) / dy - .5;

//====== Переход к оконным координатам

CPoint pt (MapToLogX(x) ,MapToLogY(y)) ;

//====== Если точка первая, то ставим перо

if (i==0)

pDC->MoveTo(pt);

else

pDC->LineTo(pt);

}

}

Вспомогательная функция

Напомним, что идеи, заложенные в алгоритме выработки цифровой метки на оси графика, принадлежат Александру Калимову, а сам алгоритм разрабатывался при его активном участии. Функция Make Label понадобилась нам в связи с тем, что переход к экспоненциальной форме числа требует некоторых усилий. Мы надеемся, что он будет происходить достаточно редко, так как алгоритм генерации цифровой метки использует методику «жизни без порядка в диапазоне семи порядков», описанную выше. Однако если все-таки диапазон изменения функции или даже координаты X выйдет за обозначенные пределы, то экспоненциальная форма неизбежна. При всем этом мы должны попытаться не делать метку слишком длинной. Экспоненциальная форма создается нами так, чтобы она была более компактной. Если доверить эту работу функциям системы, то они припишут ' знак порядка и лидирующие нули, от которых необходимо избавиться. Но если ее укоротить слишком сильно, то невозможно будет различить две соседние метки. Поэтому при определении количества необходимых разрядов мантиссы анализируется шаг сетки вдоль текущей оси графика. Вся эта черновая работа и производится в теле функции MakeLabel:

CString CGraph::MakeLabel(bool bX, doubles v) {

CString s = "0.0";

if (v == 0.)

return s;

//====== Сначала делаем грубую прикидку

//====== Пробуем поместиться в 20 позиций

s.Format("%20.10f",v);

//====== Выясняем порядок шага сетки,

//====== переворачивая его знак (трюк)

int nDigits = int(ceil(-loglO(bХ ?m_DataX.Step

: m_DataY.Step)) ) ;

//====== Если все изменения происходят до запятой,

//====== то цифры после запятой нас не интересуют

if (nDigits <= 0)

nDigits = -1;

else

if(bХ)

nDigits++; // Эстетическая добавка

//====== Слева усекаем все

s .TrimLeft () ;

//====== Справа оставляем минимум разрядов

s = s.Left(s.Find(".") + nDigits + 1);

int iPower = bX ? m_DataX.Power : m_DataY.Power;

( //====== Нужен ли порядок?

if (iPower != 0)

{

//=== Нужен, если не поместились в (10"-3, 10^А+4)

CString add;

add.Format("-e%+d",iPower);

s += add;

}

return s;

}

В настоящий момент можно запустить проект на выполнение. Вы должны увидеть распределение поля, изображенное на рис. 11.3.

Вид кривой определяется параметрами задачи, заданными нами по умолчанию. В рамках этой книги, носящей учебный характер, мы не собираемся разрабатывать достаточно серьезный инструмент для исследования решений краевых задач матфизики, однако, введя диалог по изменению параметров задачи, можем сделать нечто большее, чем просто учебный пример, иллюстрирующий использование динамических структур данных.

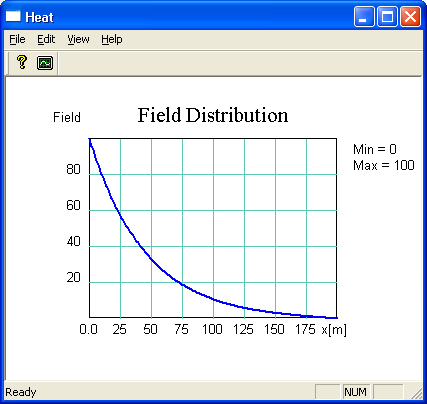
Рис. 11.3. Распределение поля для набора данных по умолчанию

Диалог для исследования решений

Сейчас мы быстрыми темпами, не углубляясь в детали, создадим диалог, работающий в немодальном режиме и позволяющий исследовать решения уравнения Пуассона при разных значениях свойств среды, произвольном расположении источников поля и произвольных граничных условиях.

Так как диалог будет вызываться по команде меню, откройте в окне редактора ресурс меню IDR_MAINFRAME и приведите его в соответствие со следующей схемой. В меню File должна быть только одна команда Exit, в меню Edit уберите все команды и вставьте одну команду Parameters, индекс (ID_EDIT_PARAMETERS) ей будет присвоен автоматически. Остальные меню оставьте без изменения. С помощью редактора диалогов создайте новое диалоговое окно (форму), которое имеет вид, изображенный на рис. 11.4. Типы элементов управления, размещенных в окне диалога, и их идентификаторы сведены в табл. 11.1. Затем создайте класс для управления диалогом.

1. Вызовите контекстное меню в форме диалога и выберите команду Add Class.
   
2. В качестве типа класса выберите MFC Class.
   
3. В окне мастера MFC Class Wizard задайте имя класса CParamDlg, базовый класс CDialog, идентификатор диалога: IDD_PARAM и нажмите кнопку Finish.
   

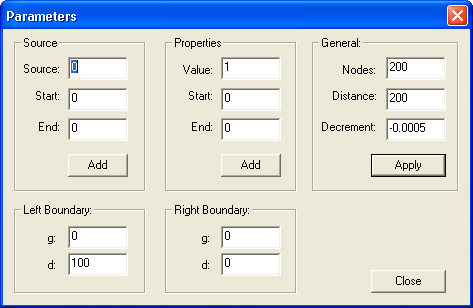
Рис. 11.4. Форма диалога для управления параметрами краевой задачи

Таблица 11.1. Идентификаторы элементов управления

Вручную введите изменения в файл с объявлением класса, так чтобы он стал: ftpragma once

class CParamDlg : public CDialog {

//===== Будем общаться с окном

friend class CChildView;

DECLARE_DYNAMIC(CParamDlg)

public:

//===== Будем помнить его адрес

CChildView *m_pView;

//===== В конструкторе запросим его адрес

CParamDlg(CChildView* р) ;

virtual ~CParamDlg () ;

// Dialog Data

enum { IDD = IDD_PARAM );

protected:

virtual void DoDataExchange(CDataExchange* pDX) ;

DECLARE_MESSAGE_MAP() );

Для всех четырех кнопок на форме диалога создайте обработчики уведомлений, или, используя терминологию Microsoft, Control Event типа BN_CLICKED. Вы помните, что это делается с помощью небольшой кнопки Control Event, которая расположена на панели инструментов окна Properties. В это окно надо входить в тот момент, когда фокус находится на соответствующей кнопке. Во всяком случае, именно так это работает в бета-версии Studio.Net.

Для обмена данными с шестью окнами редактирования (IDC_SOL)RCE, IDC_SOURCE1, IDC_SOURCE2, IDC_PROP, IDC_PROP1, IDC_PROP2) создайте с помощью мастера Add Member Variable Wizard шесть переменных:

//==== Интенсивность источника поля

double m_Source;

// Индекс ячейки сетки, где расположено начало источника

int m_Src!dl;

// Индекс ячейки сетки, где расположен конец источника

int m_Srdd2;

//==== Значение физического свойства ячейки сетки

double m_Prop;

// Индексы начала и конца области со свойством

m_Prop int m_PropIdl;

int m_PropId2;

В результате этих действий в классе CParamDlg кроме указанных переменных должны появиться шесть вызовов функции обмена данными DDX_Text, которые мастер размещает внутри функции CParamDlg::DoDataExchange. Вручную добавьте в DoDataExchange еще семь вызовов функции DDX_Text для обмена данными с переменными, которые расположены не в диалоговом, а в оконном классе (cchildview). После этого функция должна приобрести вид:

void CParamDlg::DoDataExchange(CDataExchange* pDX) {

DDX_Text (pDX, IDC_PROP2, m_Prop!d2);

DDXJText(pDX, IDC_PROP1, m_Prop!dl);

DDX_Text(pDX, IDC_PROP, m_Prop);

DDX_Text(pDX, IDC_SOURCE2, m_Srdd2);

DDX_Text(pDX, IDC_SOURCE1, ra_SrcIdl);

DDX_Text(pDX, IDC_SOURCE, m_Source);

//===== Обмен с переменными оконного класса

DDX_Text(pDX, IDC_NODES,m_pView->m__n);

DDX_Text(pDX, IDC_DIST, m_pView->m_L);

DDX_Text(pDX, IDC_DECR, m_pView->m_k);

DDX_Text(pDX, IDC_LEFTG, m_pView->m_g0);

DDX_Text(pDX, IDC_LEFTD, ra_pView->m_d0);

DDX_Text(pDX, IDC_RIGHTG, mj?View->m_gn);

DDX_Text(pDX, IDC_RIGHTD, m_pView->m_dn);

CDialog::DoDataExchange(pDX);

}

При нажатии на одну из кнопок Add в соответствующем контейнере параметров системы (m_f или m_r) должны произойти замены значений по индексам, определяемым диапазоном (m_Srddl, m_Srdd2) ИЛИ (m_Prop!dl, m_Prop!d2). В первом случае вы вводите новые источники поля, а во втором — изменяете свойства среды. В уже существующие заготовки функций обработки нажатия на кнопки введите такие коды:

void CParamDlg::OnClickedApply(void) {

//====== Считываем данные из окон

UpdateDataO ;

//====== Заново решаем систему и выводим график

m_jpView->Solve () ; }

void CParamDlg::OnClickedAddsource(void)

{

UpdateData();

//====== Изменяем контейнер m_f (источников поля)

for (int i=m_Src!dl; i <= m_Srdd2; i + + ) {

if (0 <= i && i < m_pView~>m_n)

m_pView->m_f[i] = -m_Source; )

m_pView->Solve0; }

void CParamDlg::OnClickedAddprop(void) { UpdateDataO ;

//====== Изменяем контейнер m_r (свойств среды)

for (int i=m_Prop!dl; i <= m_PropId2; i++) {

if (0 <= i &i i < m_pView->m_n && m_Prop > 0.)

m_pView->ra_r[i] = m_Prop; }

m_pView->Solve(); }

void CParamDlg::OnClickedCancel(void)

{

//====== Закрываем немодальный диалог

m_pView->m_pDlg = 0;

DestroyWindow(); }

Измените коды конструктора класса так, чтобы запоминался обратный указатель на объект оконного класса. Заодно сверьте начало файла ParamDlg.h с тем фрагментом, что приведен ниже:

#include "stdafx.h"

#include "Heat.h"

#include"ParamDlg.h"

IMPLEMENT_DYNAMIC(CParamDlg, CDialog)

CParamDlg::CParamDlg(CChildView* p)

: CDialog(CParamDlg::IDD, p)

{

m_pView = p;

//===== Начальное значение свойств среды

//===== не должно равняться нулю

m_Prop =1.0;

m_Prop!dl = 0;

m_Prop!d2 = 0;

m_Source =0.0;

m_Src!dl = 0;

m_Srdd2 = 0;

}

CParamDlg::~CParamDlg()

{

}

Инициализация диалога, как вы помните, должна производиться в обработчике сообщения WM_INITDIALOG. Здесь я опять попадаю в ловушку. В рамках Visual C++ Studio.Net вы не найдете WM_INITDIALOG в списке доступных сообщений, но вместо этого найдете функцию OnlnitDialog в списке виртуальных функций (overrides). Введите в класс CParamDlg эту функцию. В ней мы просто отодвинем окно диалога, чтобы оно при появлении на экране не заслоняло график. Другие установки должны происходить автоматически:

BOOL CParamDlg::OnInitDialog(void) {

CDialog:rOnlnitDialog();

CRect r;

//===== С помощью контекста устройства

//===== узнаем размеры всего экрана CClientDC dc(this);

int w = dc.GetDeviceCaps(HORZRES);

int h = dc.GetDeviceCaps(VERTRES);

//===== Узнаем размеры окна диалога GetWindowRect(&r);

//===== Смещаем его вправо и вниз

r.OffsetRect(w-r.right-10,h-r.bottom-30);

MoveWindow(Sr);

return TRUE;

}

В данный момент полезно запустить приложение и поучиться сражаться с ошибками, которые вызваны тем, что классы приложения не очень хорошо знакомы между собой. Добавьте директиву:

#include "ChildView.h"

в список директив файла ParamDlg.cpp, а также директиву

#include "ParamDlg.h"

в список директив файла ChildView.cpp. После этого исправления вы увидите еще одно сообщение об ошибке, которое напомнит вам о том, что еще не реализована работа с диалогом в немодальном режиме. Для этого надо немного потрудиться. Введите в класс CChildView реакцию на событие выбора пользователем команды меню ID_EDIT_PARAMETERS. Напомним, что это делается с помощью кнопки Events окна Properties. В обработчике мы открываем диалог в немодальном режиме:

void CChildView::OnEditParameters(void) {

//===== Если диалог не открыт,

if (!m_pDlg)

{

//== Динамически создаем объект диалогового класса

m_pDlg = new CParamDlg(this);

//== и после этого создаем окно диалога

m_pDlg->Create(IDD_PARAM);

}

}

В окне свойств для формы диалога установим в True свойство visible. В классе cParamDlg следует переопределить виртуальную функцию PostNcDestroy, в теле которой необходимо освободить память, занимаемую объектом диалогового класса:

void CParamDlg::PostNcDestroy(void)

{

delete this;

}

После этого диалог должен работать. Задайте точечный источник поля в узле 100, и вы увидите график решения, которое имеет вид, показанный на рис. 11.5.

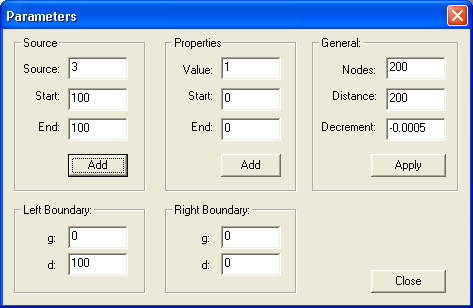
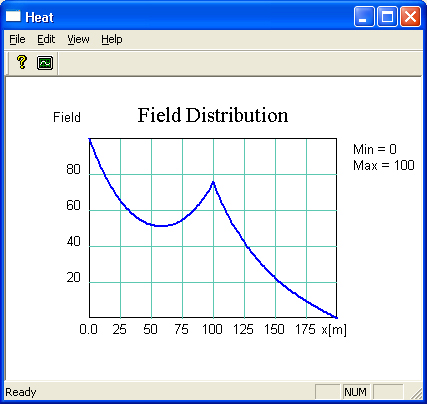
Рис. 11.5. Управление параметрами краевой задачи из диалога

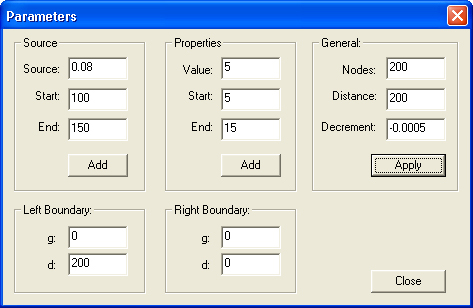
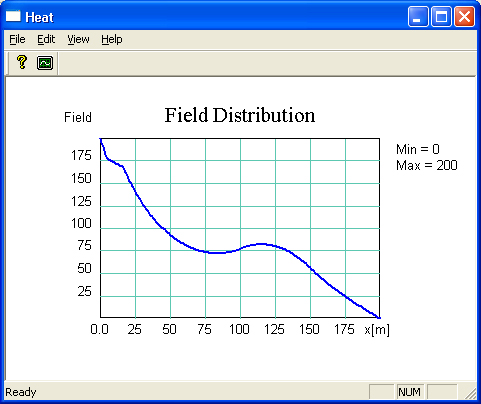
Рис. 11.6 Распределение поля в неоднородной среде при наличии осточнтков