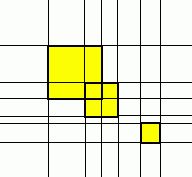
1 1 0 0 0
1 1 1 0 0
0 1 1 0 0
0 0 0 0 0
0 0 0 0 1
Задача g6_1041: Квадраты
Дано N квадратов на плоскости (1 < N < 100), причем стороны квадратов параллельны осям координат. Определить площадь области, которую определяют эти квадраты в совокупности (точка принадлежит этой области, если она находится хотя бы в одном из квадратов).
Формат входных данных
В первой строке входного файла находится число N.
В последующих N строках находятся тройки чисел (x, y, a), каждая из которых описывает один квадрат следующим образом: (x,y) - координаты центра квадрата, a - длина его стороны. Все числа - целые. -30000 < x,y < 30000. 0 < a < 1000.
Формат выходных данных
В выходной файл следует вывести площадь области, покрытой данными квадратами. Округлить значение до сотых и вывести ровно два знака после десятичной точки.
Пример ввода
3
0 0 2
1 1 2
-3 1 5
Правильный вывод для примера
32.00
Решение g6_1041:
Задача с ИМ-Y2K СамГУ. Самое неинтересное решение - создать массив 60000*60000 байт, т.е. около 3,5 Гб, но, к сожалению FP не может завести такой массив, а BP/TP тем более. Если у вас есть компьютер с хотя бы полу-гигабайтом опреативной памяти можете попробывать сжать размеры массива, т.к. нам достаточно всего одного бита для квадратика. К сожалению у моего компьютера всего 256 Мб. и тормозной винчестер, так что придется думать.
Найдем координаты левого верхнего и правого нижнего углов квадратиков. Теперь сольем все координаты в разные массивы - в один X, в другой - Y. Отсортируем эти массивы по возрастанию. У нас получится 2 набора координат по 200 штук в комплекте. Поставим им в соответствие таблицу 200*200 из элементов boolean, заполненную false.
Для каждого квадратика запустим процедуру, которая будет прорисовывать его хитроумную проекцию в таблицу. Она должны найти, каким номерам элементов отсортированных массивов с координатами соответствуют координаты левого верхенго и правого нижнего края. Двигаясь по X от номера левой координаты до номера правой и по Y от номера верхней до номера нижней будем присваивать этим элементам true - там находится один из квадратов или сегментов квадратов. (Пример приведен на рисунке, обратите внимание, что он не соответствует приведнным выше входным данным).
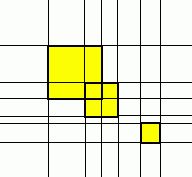 | 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 |
Теперь таблица заполнена! Осталось только посчитать площадь. Заведем цикл по всей таблице (т.е. два цикла по X и по Y). Как только нашли true, то к площади прибавляем произведение (X[I + 1] - X[I]) * (Y[J + 1] - Y[J]) ведь целочисленной координате в таблице из диапазона 1..200 соответствует целочисленное значение из -30000..30000 в отсортированном массиве координат.
Если написано слишком коряво, то напишите в гостевую книгу - переделаю.