2^n(#1021) Массивище(#1023)
#1022
Задача g6_1022: Ниточка
А.Петров, Н.Шамгунов
Злоумышленники варварски вбили в ни в чем неповинную плоскую поверхность N гвоздей, да так, что только шляпки остались. Мало того, они в своих подлых целях вбили все гвозди в вершины выпуклого многоугольника. После этого они... страшно сказать... они натянули ниточку вокруг всех гвоздей, так, что поверхности стало совсем грустно! Вот как, примерно, они это сделали:
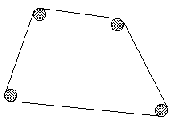Ваша задача - определить длину этой ниточки.
Ввод. В первой строке входного файла к этой задаче находятся два числа - количество гвоздей N, 1 < N < 100, и вещественное число R - радиус шляпок гвоздей. Все шляпки имеют одинаковый радиус. Далее во входном файле располагаются еще N строк, в каждой из которых записана через пробел пара вещественных координат центра очередного гвоздя; координаты не превосходят по абсолютной величине числа 100. Описания гвоздей приводятся в порядке обхода вершин многоугольника по или против часовой стрелки, начиная с произвольного гвоздя. Шляпки разных гвоздей не соприкасаются.
Вывод. Выходной файл должен в своей единственной строке содержать вещественное число, округленное до двух знаков после запятой - длину ниточки, натянутой вокруг всех гвоздей.
Пример файла input.txt.
4 1
0.0 0.0
2.0 0.0
2.0 2.0
0.0 2.0
Пример файла output.txt.
14.28
Решение g6_1022:
Заметим, что ниточка замкнута, т.е. радиус-вектор совершил полный оборот - угол в 2pi радиан. Несложно найти длину ниточки, обходящую вокруг шляпок гвоздей - 2pi*r, где r - радиус гвоздя. Если бы все гвозди были разные, то задача была бы посложнее, а так нам осталось только найти длину ниточки, соединяющей разные шляпки. В нашм случае для этого достаточно сложить расстояния между центрами гвоздей(не забыв соединить последний гвоздь с первым). Это делается очень просто S12 = sqrt(sqr(x1-x2) + sqr(y1-y2)).
Все.
Наверх