АЛГОРИТМЫ
Новости
Рассылка новостей
Форум
AlgoPascal
Редактор блок-схем
Статьи
О сайте
Контакты
Содержание - Системы линейных уравнений - Поиск фундаментальной системы решений с минимизацией невязки при помощи SVD-разложения для прямоугольной матрицыПоиск фундаментальной системы решений с минимизацией невязки при помощи SVD-разложения для прямоугольной матрицы
Для случая, когда система N линейных уравнений с N неизвестными Ax = b имеет одно и только одно решение, разработано большое число способов разрешения системы. Тем не менее, на практике иногда приходится решать системы уравнений, имеющие бесконечное число решений - в такой ситуации большинство методов откажутся работать, сообщив об ошибке. Также бывают случаи, когда система решения не имеет и надо найти лучшее приближение к нему. Также может ставиться задача поиска фундаментальной системы решений - т.е. не какого-то одного решения, а общего решения системы.
Этот алгоритм позволяет решить три проблемы - решение совместной системы, минимизацию невязки, поиск фундаментальной системы решений. Для решения используется сингулярное разложение матрицы A, т.е. её представление в виде A = U*W*V T, где U имеет размер MxN (а также ортонормированные или нулевые столбцы), W - диагональная с неотрицательными элементами на главной диагонали, V - ортонормированная размером NxN. Матрица A приводится к указанной форме, а после приведения такая система уравнений легко решается, если использовать указанные свойства матриц.
В случае, если определитель матрицы W не ноль, существует единственное точное решение, которое записывается в виде x = VW -1U T.
Если определитель ноль, то решение (или наилучшее приближение к нему) не единственно, вместо матрицы W -1 в произведении учавствует диагональная матрица D, в которой di,i = 1/wi,i , если wi,i не ноль, или di,i = 0, если wi,i ноль. Таким образом получается частное решение. Если xчастное - полученное частное решение (или приближение), Vi - столбцы матрицы V, а Ci - произвольные коэффициенты, то общее решение имеет вид
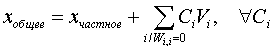
В результате работы алгоритма размерность пространства решений помещается в переменную Dimension, а само общее решение в матрицу Solutions, где в столбце с индексом 0 содержится частное решение, а в столбцах с индексом от 1 до Dimension содержатся базисные вектора общего решения.
Этот алгоритм работает примерно в 10-15 раз медленнее метода Гаусса, но обладает большей функциональностью и более устойчив при решении систем уравнений с плохо обусловленной матрицей.
Если нашли ошибку в алгоритме - сообщите!
Реализации алгоритма на различных языках:
Реализация алгоритма на C++Реализация алгоритма на DelphiРеализация алгоритма на Visual Basic 6Реализация алгоритма на AlgoPascal:
unit SVDSolveUnit;
interface SVDSolve;
implementation
const
(***********************************************
Максимальное число внутренних итераций алгоритма
Обычно сходимость уже на 7-9 итерациях. Взято с
запасом, благо скорость от этого не падает.
***********************************************)
MaxSVDIterations : Integer = 30;
(***********************************************************************
Процедура решения системы линейных уравнений вида:
A[1,1]*X[1] + .. + A[1,N]*X[N] = A[1,N+1]
....................
A[M,1]*X[1] + .. + A[M,N]*X[N] = A[M,N+1]
методом сингулярного разложения. Алгоритм решает систему уравнений и
находит фундаментальную систему решений. Матрица системы может иметь
любой ранг.
Входные данные:
A - матрица системы в столбцах с 1 по N и её правая
часть в (N+1)-ом столбце.
M - число строк в матрице (число уравнений)
N - число неизвестных
Epsilon - допуск. Если в диагональной матрице элемент на
главной диагонали по модулю меньше epsilon, то
он считается нулевым, а соответствующий ему вектор
считается базисным вектором пространства решений.
Выходные данные:
Solutions - фундаментальная система решений. Матрица размером
N*(Dimensions+1). Столбец с номером 0 содержит
частное решение системы уравнений (или решение
с минимальной невязкой, если система несовместна),
столбцы с номерами с 1 по Dimensions содержат
ортогональный набор векторов, являющихся базисом
пространства решений однородной системы.
Dimension - размерность пространства решений
Алгоритм не возвращает кода ошибки, так как при любой входной матрице
он завершается успешно.
***********************************************************************)
procedure SVDSolve(
A : array of array of Real;
M : Integer;
N : Integer;
out Solutions : array of array of Real;
out Dimension : Integer;
Epsilon : Real);
var
nm : Integer;
MinMN: Integer;
l : Integer;
k : Integer;
j : Integer;
jj : Integer;
its : Integer;
i : Integer;
z : Real;
y : Real;
x : Real;
scale: Real;
s : Real;
h : Real;
g : Real;
f : Real;
c : Real;
anorm: Real;
rv1: array of Real;
W: array of Real;
V: array of array of Real;
Flag: Boolean;
begin
////////////////////////////////////////////
//Осуществление SVD-разложения
//////////////////
SetBounds(rv1, [1, N]);
SetBounds(W, [1,N]);
SetBounds(V, [1,N], [1,N]);
if M<N then
MinMN:=M
else
MinMN:=N;
g := 0.0;
scale:=0.0;
anorm:=0.0;
for i:=1 to n do
begin
l:=i+1;
rv1[i]:=scale*g;
g:=0;
s:=0;
scale:=0;
if i<=m then
begin
for k:=i to m do
scale:=scale+AbsReal(a[k,i]);
if scale<>0.0 then
begin
for k:=i to m do
begin
a[k,i] := a[k,i]/scale;
s := s+a[k,i]*a[k,i]
end;
f:=a[i,i];
g:=-ExtSign(sqrt(s),f);
h:=f*g-s;
a[i,i]:=f-g;
if i<>n then
begin
for j:=l to n do
begin
s:=0.0;
for k:=i to m do
s:=s+a[k,i]*a[k,j];
f:=s/h;
for k:=i to m do
a[k,j] := a[k,j]+f*a[k,i];
end;
end;
for k:=i to m do
a[k,i] := scale*a[k,i];
end;
end;
w[i]:=scale*g;
g:=0.0;
s:=0.0;
scale:=0.0;
if (i<=m) and (i<>n) then
begin
for k:=l to n do
scale:=scale+AbsReal(a[i,k]);
if scale<>0.0 then
begin
for k:=l to n do
begin
a[i,k]:=a[i,k]/scale;
s:=s+a[i,k]*a[i,k];
end;
f:=a[i,l];
g:=-ExtSign(sqrt(s),f);
h:=f*g-s;
a[i,l]:=f-g;
for k:=l to n do
rv1[k] := a[i,k]/h;
if i<>m then
begin
for j:=l to m do
begin
s:=0.0;
for k:=l to n do
s:=s+a[j,k]*a[i,k];
for k:=l to n do
a[j,k]:=a[j,k]+s*rv1[k];
end;
end;
for k:=l to n do
a[i,k]:=scale*a[i,k];
end;
end;
anorm:=MyMax(anorm,(AbsReal(w[i])+AbsReal(rv1[i])))
end;
for i:=n downto 1 do
begin
if i<n then
begin
if g<>0.0 then
begin
for j:=l to n do
v[j,i] := (a[i,j]/a[i,l])/g;
for j:=l to n do
begin
s:=0.0;
for k:=l to n do
s:=s+a[i,k]*v[k,j];
for k:=l to n do
v[k,j]:=v[k,j]+s*v[k,i];
end;
end;
for j:=l to n do
begin
v[i,j]:=0.0;
v[j,i]:=0.0;
end;
end;
v[i,i]:=1.0;
g:=rv1[i];
l:=i;
end;
for i:=MinMN downto 1 do
begin
l:=i+1;
g:=w[i];
if i<n then
begin
for j:=l to n do
a[i,j]:=0.0;
end;
if g<>0.0 then
begin
g:=1.0/g;
if i<>n then
begin
for j:=l to n do
begin
s := 0.0;
for k:=l to m do
s:=s+a[k,i]*a[k,j];
f:=(s/a[i,i])*g;
for k:=i to m do
a[k,j]:=a[k,j]+f*a[k,i];
end;
end;
for j:=i to m do
a[j,i]:=a[j,i]*g;
end
else
begin
for j:=i to m do
a[j,i]:=0.0;
end;
a[i,i]:=a[i,i]+1.0;
end;
for k:=n downto 1 do
begin
for its:=1 to MaxSVDIterations do
begin
Flag:=True;
for l:=k downto 1 do
begin
nm:=l-1;
if (AbsReal(rv1[l])+anorm)=anorm then
begin
Flag:=False;
Break;
end;
if (AbsReal(w[nm])+anorm)=anorm then
begin
Break;
end;
end;
if Flag then
begin
c:=0.0;
s:=1.0;
for i:=l to k do
begin
f:=s*rv1[i];
if (AbsReal(f)+anorm)<>anorm then
begin
g:=w[i];
h:=Pythag(f,g);
w[i]:=h;
h:=1.0/h;
c:=g*h;
s:=-(f*h);
for j:=1 to m do
begin
y:=a[j,nm];
z:=a[j,i];
a[j,nm]:=(y*c)+(z*s);
a[j,i]:=-(y*s)+(z*c);
end;
end;
end;
end;
z:=w[k];
if l=k then
begin
if z<0.0 then
begin
w[k]:=-z;
for j:=1 to n do
v[j,k]:=-v[j,k];
end;
Break;
end;
x:=w[l];
nm:=k-1;
y:=w[nm];
g:=rv1[nm];
h:=rv1[k];
f:=((y-z)*(y+z)+(g-h)*(g+h))/(2.0*h*y);
g:=Pythag(f,1);
f:=((x-z)*(x+z)+h*((y/(f+ExtSign(g,f)))-h))/x;
c:=1.0;
s:=1.0;
for j:=l to nm do
begin
i:=j+1;
g:=rv1[i];
y:=w[i];
h:=s*g;
g:=c*g;
z:=Pythag(f,h);
rv1[j]:=z;
c:=f/z;
s:=h/z;
f:=(x*c)+(g*s);
g:=-(x*s)+(g*c);
h:=y*s;
y:=y*c;
for jj:=1 to n do
begin
x:=v[jj,j];
z:=v[jj,i];
v[jj,j]:=(x*c)+(z*s);
v[jj,i]:=-(x*s)+(z*c)
end;
z:=Pythag(f,h);
w[j]:=z;
if z<>0.0 then
begin
z:=1.0/z;
c:=f*z;
s:=h*z;
end;
f:=(c*g)+(s*y);
x:=-(s*g)+(c*y);
for jj:=1 to m do
begin
y:=a[jj,j];
z:=a[jj,i];
a[jj,j]:=(y*c)+(z*s);
a[jj,i]:=-(y*s)+(z*c)
end;
end;
rv1[l]:=0.0;
rv1[k]:=f;
w[k]:=x;
end;
end;
////////////////////////////////////////////
//Решение полученной системы уравнений:
//////////////////
Dimension:=0;
for I:=1 to N do
if AbsReal(W[I])<Epsilon then
Dimension:=Dimension+1;
SetBounds(Solutions, [1,N], [0,Dimension]);
//Transonse(U)*b
for I:=1 to N do
begin
Solutions[I,0]:=0;
for J:=1 to M do
Solutions[I,0]:=Solutions[I,0]+A[J,I]*A[J,N+1];
end;
//V*diag(1/w) и собираем базис решений
K:=1;
for J:=1 to N do
if AbsReal(W[J])>Epsilon then
begin
for I:=1 to N do
V[I,J]:=V[I,J]/W[J];
end
else
begin
for I:=1 to N do
Solutions[I,K]:=V[I,J];
K:=K+1;
end;
//получаем частное решение
//используем первую строку матрицы как временную переменную
for I:=1 to N do
begin
A[1,I]:=0;
for J:=1 to N do
if AbsReal(W[J])>Epsilon then
A[1,I]:=A[1,I]+V[I,J]*Solutions[J,0];
end;
for I:=1 to N do
Solutions[I,0]:=A[1,I];
end;
(************************************************************
Служебные подпрограммы
************************************************************)
function ExtSign(a:Real; b: Real):Real;
begin
if b>=0 then
Result:=AbsReal(a)
else
Result:=-AbsReal(a);
end;
function MyMax(a:Real; b:Real):Real;
begin
if a>b then
Result:=a
else
Result:=b;
end;
function Pythag(A:Real; B:Real):Real;
begin
if AbsReal(A)<AbsReal(B) then
Result:=AbsReal(B)*Sqrt(1+Sqr(A/B))
else
Result:=AbsReal(A)*Sqrt(1+Sqr(B/A));
end;
end.
Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU