Структуры данных.

Автор:Быстрицкий В.Д.

• Массивы.
• Связные списки.
• Стек.
• Деревья.
• Графы.

При разработке программ часто приходится решать вопрос, какие структуры использовать для хранения информации. Причем от выбора структуры данных зависит скорость написания и то насколько легко и быстро Вы сможете впоследствии модифицировать работу уже созданной программы. Я попытаюсь систематизировать в одной статье, часто используемые структуры.

Следует так же понимать, как любая из используемых структур реализуется конкретным языком программирования. Нельзя забывать, что иногда удобство написания программ может привести к существенным увеличениям затрат машинных ресурсов, а следовательно, к замедлению работы программы и ее повышенной требовательности к параметрам компьютера.

Массивы.

Начнем с наиболее часто используемой структуры, которая реализована практически во всех современных языках, а именно с массивов. Под массивом я буду понимать множество элементов одного типа, проиндексированный при помощи набора натуральных чисел. При этом следует сразу заметить, что я не оговариваю природу элементов (т.е. элементами массива могут быть целые или действительные числа, строки или нечто совсем экзотическое). Ограничим рассмотрение одномерными массивами (многомерные массивы можно получить из данного определения, предполагая, что элементы, наполняющие массив, сами являются массивом).

Основное отличие массивов от других структур - это возможность быстрого доступа к произвольному элементу, используя только его номер по порядку. При этом отсутствует необходимость просмотра других элементов массива. Второе отличие - фиксированное количество элементов массива (я не рассматриваю здесь разного рода нововведения, например, открытые массивы). Это кажется существенным ограничением, и иногда приводит к невозможности использования массивов для реализации тех или иных алгоритмов. Но с другой стороны существует большое число задач, в которых использование массивов возникает как естественное и единственно правильное решение. В качестве примера можно привести математические задачи: работа с матрицами, табличное задание функций и т.п., в этих задачах возможность доступа к элементам, используя индексную адресацию, важна, а фиксированное количество элементов не имеет значения.

Связные списки.

При программировании практических задач часто приходится работать с различными списками. Каждый элемент списка имеет, как правило, составную структуру. Для реализации списков можно использовать массивы, но существует ограничение присущие массивам (или любой структуре, которая хранит элементы в памяти последовательно), а именно:

Допустим, мы составили список работников некоего предприятия. При этом для удобства, упорядочили его относительно фамилий работников. Но вот один из работников уволился, и теперь нам необходимо удалить его запись из списка, эта простейшая задача приводит к серьезным проблемам: мало просто стереть запись, надо сдвинуть вперед все элементы идущие следом за удаляемым. Та же проблема "с точностью до наоборот" возникает при внесении нового элемента в список. В этом случае лучше использовать в качестве структуры хранения информации связный список.

В связном списке каждый элемент содержит одно (односвязный список) или два (двусвязный список) дополнительных поля - поля связи со следующим элементом, а для двусвязного списка и с предыдущим элементом. Дополнительно для определения связного списка необходима переменная (FIRST) для хранения указателя на первый элемент списка (для двусвязного списка дополнительно переменная (LAST) для хранения указателя на последний элемент) и некий символ (NIL) для указателя "в никуда". На рисунке представлена схема одно - и двусвязного списка.

Связные списки существенно облегчают задачи удаления элемента (достаточно просто переставить связи) и вставки нового элемента (опять достаточно внести изменения только в поле связи одного элемента). Так же намного проще становиться изменить порядок следования элементов (например при необходимости упорядочить список). Но при этом получить доступ к элементу с определенным номером, становиться существенно сложнее (необходимо пройти все предшествующие элементы). Сложность возникает и при необходимости просто подсчитать количество элементов в списке, для этого необходимо пройти весь список.

Стек.

В качестве примера односвязного списка рассмотрим стек. Механизм функционирования стека хорошо отражает другое его название - список типа «LIFO» (last in first out - «последним вошел - первым вышел»). При работе со стеком предполагаются только две операции: занесение элемента в вершину стека и удаление элемента, находящегося в вершине стека. Таким образом, операция удаления элемента из стека применима только к элементу, помещенному на стек последним. А значит, любой элемент не может удален из стека раньше, чем будут удалены все элементы, помещенные в стек после него.

Примером применение стека служит задача проверки правильности расстановки скобок. Проходя выражение слева направо, мы, при появлении открывающей скобки, помещаем ее в стек, а в случае появления закрывающей скобки пытаемся удалить элемент с вершины стека. Если в ходе работы возникает ситуация, когда стек пуст, а мы имеем закрывающую скобку, то это означает, что выражение составлено не правильно. В конце работы стек должен быть пуст, иначе мы так же делаем вывод о несоответствии скобок в выражении.

Деревья.

Формально деревья можно определить как конечное множество A, состоящие из одного или более узлов таких, что:   1. имеется один узел, называемый корнем дерева,   2. остальные узлы (кроме корня) содержаться в m > 0 попарно не пересекающихся множествах A₁, . . . , A_m, каждое из которых в свою очередь является деревом.

Деревья, как правило, дают хорошие представление о структуре отношения между элементами данных. Например, на рисунке показано дерево, представляющие формулу: (ab+cd)/bc.

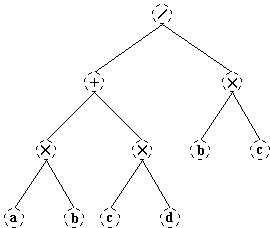
Один из классов деревьев следует выделить особо - это класс бинарных деревьев. Формально бинарное дерево - конечное множество узлов, которое либо пусто, либо состоит из корня и двух бинарных деревьев. Предыдущий рисунок пример дерева как раз такого класса.

При работе с деревьями часто приходится решать задачу обхода дерева. Для этого удобно использовать например такой рекурсивный алгоритм:

	1. Корень дерева.
	2. Если нет поддеревьев, то ВЫХОД, 
			иначе обходим все поддеревья слева направо.

Интересный способ реализации бинарных деревьев можно посмотреть в алгоритме сортировки массива методом Уильяма-Флойда.

Графы.

Графы - обобобщение структуры деревьев. Формально граф - пара G=(V,E), где V - множество объектов произвольной природы, называемых вершинами, а E - семейство пар e_i=(v_i1, v_i2), v_ij из V, называемых ребрами. Возможны случаи кратных ребер, но мы не будем на них останавливаться. Можно рассматривать взвешенные и невзвешенные, ориентированные и неориентированные графы. Граф, в котором нет кратных ребер, можно задать при помощи весовой матрицы. Для каждой пары вершин в матрице указывается вес ребра соединяющего вершины (если ребра нет, то полагаем соответствующий элемент матрицы равным бесконечности). Матрица может быть несимметричной в случае ориентированного графа.

В случае не взвешенного графа удобнее представлять его при помощи матрицы связности, элемент которой равен 1, если есть соответствующие ребро и 0, если ребро отсутствует.

Пример использования графа - это например задание условий в проблеме коммивояжера, здесь населенные пункты помещаются в вершины графа, а веса ребер определяют расстояние между соответствующими населенными пунктами.

Теория графов достаточно обширна и многие алгоритмы, рассматриваемые в ней, имеют интерес сами по себе. Для решения прикладных задач часто возникает необходимость определить связаны ли две вершины графа, а в случае наличия весов определить вес пути между ними. Некоторые из алгоритмов представлены у меня на странице теории графов, но при желании более углублено рассмотреть эту структуру, я настоятельно рекомендую обратиться к соответствующей литературе.

Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU