АЛГОРИТМЫ

Новости

Рассылка новостей

Форум

AlgoPascal

Редактор блок-схем

Статьи

О сайте

Контакты
Содержание - Системы линейных уравнений - Метод ортогонализации для прямоугольной матрицы с минимизацией невязки, заданной квадратичной формой

Решение СЛАУ с прямоугольной матрицей методом ортогонализации с минимизацией невязки, заданной квадратичной формой

Этот алгоритм является развитием предыдущего. Оригинальный алгоритм решал системы из N уравнений с N неизвестными (Ax=b), минимизируя норму невязки решения. В качестве нормы невязки брался скалярный квадрат вектора verror  = Ax-b.

В новом алгоритме M уравнений, N неизвестных (M < N, M=N или M > N) а норма невязки задается формулой verror  = (Ax-b) TP(Ax-b), где P - симметричная матрица размером NxN.

Алгоритм практически не изменился. В паре мест изменились индексы, по которым ведется суммирование (это из-за изменения размера матрицы), скалярное произведение теперь вычисляется при помощи умножения векторов и матрицы. К сожалению, алгоритм стал существенно медленнее - он требует порядка N 4 операций (скалярное произведение считается в N раз медленнее).

В принципе, эта задача может быть решена и по-другому: перейти к базису, в котором матрица P является единичной, при помощи преобразования Q такого, что Q TPQ = E. Затем решить систему уравнений (QA)x=Qb при помощи предыдущего алгоритма. Такой способ будет быстрее, так как будет требовать порядка N 3 операций на решение системы уравнений и ещё некоторое количество на итерационный поиск требуемого преобразования.

Проблема точности

Есть одна тонкость, которую следует обсудить. В формуле ортогонализации есть дробь, в знаменателе которой находится скалярный квадрат вектора bi . Если система векторов A линейно-зависима, то в одной из таких дробей в знаменателе окажется ноль. Решая задачу аналитически, мы просто отбросим нулевой вектор и продолжим процесс без него. Но при численном решении полученный вектор будет очень близок к нолю, но не равен ему из-за погрешностей при расчетах. Поэтому вместо проверки на равенство нолю надо проводить проверку на близость к нолю, и если вектор ближе заданной величины epsilon, то мы считаем его нулевым.

Тем не менее, при таком подходе возможно как ненахождение существующего решения, так и нахождение несуществующего. Рассмотрим это на примере:

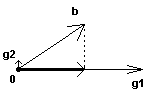
Пусть ортогонализируя матрицу A, мы получили два ортогональных вектора g1  и g2 . Правая часть системы равна b. Вектор g2  намного меньше вектора g1 . Вполне возможно, что он неравен нолю из-за возникшей при расчетах погрешности. Если мы не отбросим его (выбрав слишком малое epsilon), то сможем разложить вектор b по базису G и получим ошибочное решение. Т.е. система уравнений несовместна, а точное решение как будто бы существует. Разумеется, в результате мы получим мусор, а не решение.

Возможна и другая ошибка - мы выбрали слишком большое epsilon и отбросили вектор g2 , хотя этот вектор не равен нолю и не близок к нему. Тогда вместо вектора b мы получим только его проекцию на ось g1 , и решение будет ошибочным - мы заключим, что система несовместна, хотя она на самом деле совместна.

Одним из узких мест в работе метода ортогонализации является именно принятие решения о том, выражается ли один вектор через другой или нет. Именно здесь, если задать слишком малое epsilon, и возникают ошибки, искажающие решение. Если epsilon слишком мало, то при делении на него получаются слишком большие числа, которые просто переполняют разрядную сетку, что приводит к гигантской потере точности. К сожалению, нельзя дать никаких общих рекомендаций относительно выбора величины epsilon, так как её оптимальный выбор зависит от входных данных. Здесь всё зависит только от программиста.

Если нашли ошибку в алгоритме - сообщите!


Реализации алгоритма на различных языках:

Реализация алгоритма на C++
Реализация алгоритма на Delphi
Реализация алгоритма на Visual Basic 6

Реализация алгоритма на AlgoPascal:

unit MinimalMisclosureRectCustomUnit;

interface MinimalMisclosureRectCustomSolve;

implementation
(*******************************************************************
function MinimalMisclosureRectCustomSolve(
            A   :   array [1..M, 1..N+1] of Real;
            P   :   array [1..M, 1..M]   of Real;
    const   M   :   Integer;
    const   N   :   Integer;
    out     X   :   array [1..N]         of Real;
    const   Epsilon : Real):Boolean;

Функция решения системы линейных уравнений вида:
A[1,1]*X[1] + .. + A[1,N]*X[N] = A[1,N+1]
        ....................
A[M,1]*X[1] + .. + A[M,N]*X[N] = A[M,N+1]
с минимизацией вектора невязки.

Величина вектора невязки определяется, как скалярный  квадрат  этого
вектора. Функция скалярного произведения задается матрицей P,  пере-
даваемой в алгоритм, где P[I,J] равно скалярному произведению  I-ого
и J-ого базисных векторов. Таким  образом,  матрица  P  должна  быть
симметричной.

Функция   возвращает   True,   если  система уравнений имеет  точное
решение, и False, если система не имеет точного решения.
Вектор X содержит в себе точное решение (или одно из решений)    или
решение  с  минимальной невязкой при отсутствии точного решения.

Epsilon определяет, насколько столбец должен отличаться от ноля, чтобы
считаться неравным нолю и учавствовать в разложении других столбцов в
качестве базисного вектора.
*******************************************************************)
function MinimalMisclosureRectCustomSolve(
            A   :   array of array of Real;
            P   :   array of array of Real;
    const   M   :   Integer;
    const   N   :   Integer;
    out     X   :   array of Real;
    const   Epsilon : Real):Boolean;
var
    I               :   Integer;
    I2              :   Integer;
    J               :   Integer;
    K               :   Integer;

    L1              :   Real;

    IsBasisVector   :   array of Boolean;

    E               :   array of array of Real;
    C               :   array of Real;
begin
    SetBounds(IsBasisVector, [1,N+1]);
    SetBounds(X, [1,N]);
    SetBounds(C, [1,M]);

    //установим единичную матрицу, добавим фиктивный N+1-ый столбец
    SetBounds(E, [1,N], [1,N+1]);
    for I:=1 to N do
        for J:=1 to N do
            if I=J then
                E[I,J] := 1
            else
                E[I,J] := 0;
                
    //сохраним последний столбец
    for I:=1 to M do
        C[I]:=A[I,N+1];

    //ортонормируем систему стобцов
    for J:=1 to N+1 do
    begin
        for K:=1 to J-1 do
        begin
            if not IsBasisVector[K] then
                Continue;

            L1 := 0;
            for I:=1 to M do
                for I2:=1 to M do
                    L1 := L1+A[I,K]*A[I2,J]*P[I,I2];

            for I:=1 to M do
                A[I,J] := A[I,J]-A[I,K]*L1;
            for I:=1 to N do
                E[I,J] := E[I,J]-E[I,K]*L1;
        end;

        L1:=0;
            for I:=1 to M do
                for I2:=1 to M do
                    L1 := L1+A[I,J]*A[I2,J]*P[I,I2];
        L1:=Sqrt(L1);
        IsBasisVector[J] := L1>=Epsilon;
        
        if IsBasisVector[J] then
        begin
            for I:=1 to M do
                A[I,J] := A[I,J]/L1;
            for I:=1 to N do
                E[I,J] := E[I,J]/L1;
        end;
    end;

    //точное ли решение
    Result := not IsBasisVector[N+1];
    
    //вывод решения
    for I:=1 to N do
        X[I] := 0;
    for J:=1 to N do
    begin
        if not IsBasisVector[J] then
            Continue;

        L1:=0;
        for I:=1 to M do
            for I2:=1 to M do
                L1:=L1 + A[I,J]*C[I2]*P[I,I2];
        for I:=1 to N do
            X[I]:=X[I] + L1*E[I,J];
    end;

end;

end.

 


Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU