АЛГОРИТМЫ

Новости

Рассылка новостей

Форум

AlgoPascal

Редактор блок-схем

Статьи

О сайте

Контакты
Содержание - Системы линейных уравнений - Метод Крамера

Решение СЛАУ методом Крамера

Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными:

a1,1 x1 +a1,2 x2 + ... +a1,n xn  = a1,n+1 
a2,1 x1 +a2,2 x2 + ... +a2,n xn  = a2,n+1 
.....
an,1 x1 +an,2 x2 + ... +an,n xn  =an,n+1 

Процедура позволяет найти решение, если определитель основной матрицы A=(aij ) не равен нулю. Для нахождения i-ой компоненты корня ищем определитель:

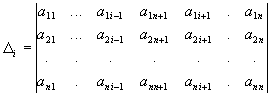
для всех i = 1..n. Тогда

В алгоритме вызывается функция вычисления определителя, в качестве которой можно использовать функцию приведенную здесь или другую имеющуюся у Вас. При сравнении определителя с нолем на самом деле проводится сравнение определителя с малым числом epsilon, передаваемым в алгоритм. Это же число передается алгоритму расчета определителя.

Если нашли ошибку в алгоритме - сообщите!


Реализации алгоритма на различных языках:

Реализация алгоритма на C++
Реализация алгоритма на Delphi
Реализация алгоритма на Visual Basic 6

Блоксхемы:

Посмотреть блок-схему алгоритма
Скачать блок-схему алгоритма

Реализация алгоритма на AlgoPascal:

unit LESKramerUnit;

declaration

(*******************************************************************
Функция расчёта определителя матрицы A[1..N,1..N].
Принимает матрицу A, размер матрицы, точность расчётов.
Число, меньше Epsilon, считается равным 0.
*******************************************************************)
function Det(A:array of array of Real; N:Integer; Epsilon:Real):Real;

interface LESKramerSolve;


implementation

(*******************************************************************
Функция решения системы линейных уравнений вида:
A[1,1]*X[1] + .. + A[1,N]*X[N] = A[1,N+1]
        ....................
A[N,1]*X[1] + .. + A[N,N]*X[N] = A[N,N+1]

Функция   возвращает   True,   если    det(A')<>0
(Х хранит решение), и False если det(A')=0,     в
таком случае X не хранит решение.
A' - матрица из первых N столбцов матрицы A.

Epsilon определяет точность сравнения чисел. Если
число по модулю меньше или равно Epsilon, то оно
считается равным 0. Это число позволяет указать
алгоритму, насколько именно переданная в него матрица
должна быть близка к вырожденной, чтобы вызвать выход
со значением True.

Чтобы проводить вычисления независимо от того, насколько
матрица близка к вырожденной, следует задать epsilon
равным 0.
*******************************************************************)

function LESKramerSolve(
            A   :   array of array of Real;
    const   N   :   Integer;
    out     X   :   array of Real;
    const   Epsilon : Real):Boolean;
var
    I   :   Integer;
    J   :   Integer;

    D   :   Real;
    DT  :   Real;
    B   :   array of array of Real;
begin
    SetBounds(X, [1,N]);
    SetBounds(B, [1,N], [1,N]);
    Result := False;
    for I:=1 to N do
        for J:=1 to N do
            B[I,J] := A[I,J];
    D:=Det(B, N, Epsilon);

    if AbsReal(D)>Epsilon then
    begin
        Result:=True;
        for I:=1 to N do
            for J:=1 to N do
                b[i,j]:=a[i,j];

        for I:=1 to N do
            b[i,1]:=a[i,n+1];

        for I:=2 to N do
        begin
            DT:=Det(B, N, Epsilon);
            x[i-1]:=DT/D;

            for J:= 1 to N do
            begin
                b[j,i-1]:=a[j,i-1];
                b[j,i]:=a[j,n+1];
            end;
        end;
        
        DT:=Det(B, N, Epsilon);
        x[n]:=DT/D;
    end;
end;

end.

 


Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU