
АЛГОРИТМЫ
Новости
Рассылка новостей
Форум
AlgoPascal
Редактор блок-схем
Статьи
О сайте
Контакты
Булева алгебра выпуклых полигонов
Автор: Павлов Дмитрий
- Введение
- Задачи приводящие к построению булевых операций над полигонами.
- Структуры данных.
- Поиск точек пересечения.
- Пересечение полигонов.
- Разность полигонов.
- Объединение полигонов.
- Оценка сложности
Введение
Постановка задачи: Построение булевой алгебры над различными типами полигонов и ее реализация.
Определение 1: Полигоном называется конечная упорядоченная последовательность точек плоскости {(xn, yn )} n=0,1,2,...N. При этом сами точки (xn, yn ) называются вершинами полигона. Ребрами полигона или границей, называются вектора (xn- xn-1, уn- уn-1 ) n=1,...,N. Точка называется внутренней точкой полигона, если почти все лучи выходящие из этой точки пересекают границу нечетное число раз.
Это самое общее определение полигона. Однако на практике приходится сталкиваться с частными случаями полигонов. Работа посвящена, как раз рассмотрению этих важных частных случаев.
Определение 2: Полигон называется простым, если множество точек пересечения ребер полигона между собой пусто.
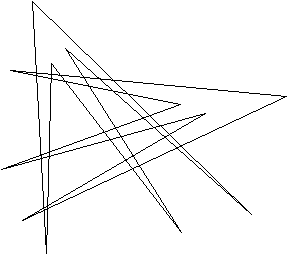
Здесь алгоритм нахождения точек пресечения требует количество операций порядка O(LM), где L число вершин в первом полигоне, M во втором полигоне. Вообще сложность операции нахождения точек пересечения полигонов, определяет сложность построения всех булевых операций. Для любых четных L и M можно построить примеры полигонов, у которых каждое ребро первого полигона пересекаются со всеми ребрами второго полигона (рис 1.), что покаэывает неулучшаемость оценки O(LM) для построения алгебры простых полигонов. (Можно ли построить соответствующие примеры для нечетного L и четного M? для нечетных L и М?)
|
| Рис. 1 |
Определение 3: Простой полигон называется выпуклым, если z[а,b]>0, где а=(xn- xn-1, уn- уn-1 ), b=(xn+1- xn, уn+1- уn ), n=1...N. (Сложение индексов происходит как в группе ZN+1).
Для выпуклых полигонов существует весьма оригинальный алгоритм нахождения точек пересечения, имеющий сложность O(L+M). Таким образом, все булевы операции над выпуклыми полигонами реализуются за линейное время.
Результаты булевых операций над выпуклыми и простыми полигонами выводят нас из класса простых полигонов, и приводят нас к понятию полигона с дырой.
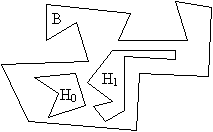
Определение 4: Полигон с дырами это множество полигонов Р={B, H0,H1, H2,...,HS}, где полигон B содержит Hi для всех i=0,...,S, называется внешним полигоном, а полигоны Hi, i=0,...,S со свойством Hi З Hj = Ж i,j=0..S, называются дырами. Точка является внутренней для полигона с дырой, если она принадлежит нечетному числу полигонов из Р.
Пример полигона с дырой приведен на рисунке 2.
|
| Рис. 2 |
Пусть есть два полигона с дырами и Р={B, H0,H1, H2,...,HS}, Q={D, G0,G1, G2,...,GK}. Оценим количество действий, необходимых для построения булевых операций. Пусть b количество вершин в полигоне В, d количество вершин в полигоне D, hi количество вершин в дыре Hi, gi количество вершин в дыре Gi.
Пусть H=max{hi,b} i=0..S, G=max{ gj,d} j=0..K. Тогда количество действий достаточных для реализации какой либо операции оценивается, как O(SKHG).
Задачи приводящие к построению булевых операций над полигонами.
Задача 1. Картография.
Дано: Имеется карта губернии города N. Имеется карта лесов Российского государства.
Требуется: Oпределить есть ли леса в губернии города N, если есть где расположены?
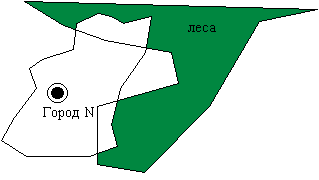
Рисунок 3 иллюстрирует данную ситуацию. Для решения необходимо, чтобы карты губернии и лесов были заданы как полигоны, далее, очевидно, надо взять их пересечение.
|
| Рис. 3 |
Задача 2. Движение какого либо виртуального объекта по дисплею.
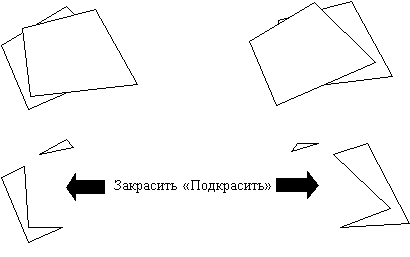
Предположим, что объект задан как полигон и уже отрисован. В момент времени t0 он находится в некотором положении (рис. 4). Чтобы отобразить объект в следующий момент времени, нет необходимости заново его отрисовывать. Необходимо найти разность старого положения и нового и закрасить цветом фона. Затем найти разность нового положения и старого и "подкрасить" объект.
|
| Рис. 4 |
Таким образом, есть возможность добиться более качественной анимации(?).
При этом если движение объекта предсказуемо, то предсказуемо и какие ребра старого полигона пересекутся с ребрами нового полигона. То есть в случае простых полигонов, например, можно уйти от оценки O(LM) для нахождения разности, что делает перерисовку объекта еще более быстрой.
На этом круг задач приводящих к построению булевых операций не исчерпывается. Желающие смогут найти несколько примеров подобного рода в книге Препараты и Шеймоса "Вычислительная геометрия".
Замечание:Знак (?) будет означать, что автор не до конца уверен в истинности данного утверждения
Структуры данных
Прежде чем приступить к описанию алгоритмов построения алгебры, остановимся на структурах данных, использовавшихся при этом. Ниже приведены структура sList и класс CPolygon.
struct sList
{
CPoint pointList;// Координаты вершины
BOOLEAN bTop; //Вершина собсвенная или добавленная
BOOLEAN bUsed; // Использовалась или нет
double z;
sList *pList; //Указатель на следующую вершину
sList *prevList; //Указатель на предыдущую вершину
};
Cтруктура sList хранит список вершин и представляет собой двусвязанную динамическую структуру данных.
class CPolygon
{
BOOLEAN bInit; // полигон задан или нет
sList *flist,*elist; //Указатели на первую и последнюю вершину
public:
long int nTop; //Число вершин (начинается с 0)
CPolygon() //Конструктор
{
nTop=-1;bInit=FALSE;
flist=elist=NULL;
}
sList *Init(sList *p); //Инициализация полигона
void Free();//Освобождение полигона
BOOLEAN GetbInit() {return bInit;}
void Show(CClientDC* p,COLORREF c);
void Show(CClientDC* pDC,COLORREF cl,int nWidthPen);
BOOLEAN GetbInit() {return bInit;}
void SetbInitFalse() {bInit=FALSE;}
sList *GetfList() {return flist;}
sList *GeteList() {return elist;}
void SeteList(sList *pe) {elist=pe;elist->pList=NULL;}
BOOLEAN PointBelong(CPoint point); // Принадлежность точки полигону как замкнутуму подмножеству R2
BOOLEAN PointBelong(CPoint point,BOOLEAN bFr); // Принадлежность точки полигону как открытому подмножеству R2
BOOLEAN PointBelong(double xt,double yt); // Принадлежность точки с рациональными координатами полигону
BOOLEAN PointBelongFr(CPoint point); //Принадлежность границе
void PlusVector(int dx,int dy); //Параллельный перенос полигона
void DelFalseTop();//Удалить из полигона точки пересечения
BOOLEAN OrientRight();//Ориентация правая или нет
void ChangeOrient();//Поменять ориентацию
void Circle() //Замкнуть полигон
{
if (nTop<0) return;
flist->prevList=elist;
elist->pList=flist;
}
void UnCircle() //Разомкнуть полигон
{
if (nTop<0) return;
flist->prevList=NULL;
elist->pList=NULL;
}
};
Замечание: Здесь и в дальнейшем, чтобы не загромождать основную идею алгоритмов, приводятся несколько упрощенные структуры данных, чем те, что используются в реальной программе.
Чтобы "вдохнуть жизнь" в полигон, необходимо сначала его инициализировать, то есть вызвать метод Init(sList *p). Параметром этого метода служит начало списка вершин.
Далее опишем класс CTwoPolygons, где мы и будем выполнять все наши булевы операции.
class CTwoPolygons
{
sList *pfInter,*peInter;//Список вершин с результатом операции
public:
CPolygon a,b; //Полигоны над которыми выполняются операции
BOOLEAN bTwoInit; //Истина, если полигоны a и b инициализированы, Ложь в противоположном случае
CTwoPolygons()
{
bTwoInit=FALSE;
pfInter=poInter=peInter=NULL;
}
int InsertCutPoint(); //Вставляет точки пересечения полигонов a и b, в оба полигона.
//Возвращает число вставленных точек.
int FindCutPoint(); //Возвращает число точек пересечения
sList *Intersection(); //Формирует список с пересечением
sList *Trim(); //Формирует список с разностью
sList *Weld();(); //Формирует список с объединением
BOOLEAN Ainsideb(); // а внутри b
BOOLEAN Binsidea(); //b внутри а
void OperationFree(); //Освобождение списка с результатом операции
};
Результаты операций даже над выпуклыми полигонами выводят нас из класса полигонов. Поэтому необходимо иметь класс, который бы умел принимать результаты булевых операций.
Ниже описывается структура sOperationPolygon и класс CResult.
struct sOperationPolygon
{
CPolygon polygon;
int typePolygon; //1-внешний полигон, 0-дырка
BOOLEAN bUsed; //Использовался или нет
sOperationPolygon *pOPolygon; //Указатель на следующий полигон
};
Структура sOperationPolygon представляет собой односвязанный список полигов.
class CResult
{
sOperationPolygon *pfOperation; // Первый полигон в списке
sOperationPolygon *peOperation; // Последний полигон в списке
BOOLEAN bInitResult; // Список пуст или нет
int nComponent; // Длина списка
public:
CResult()
{
pfOperation=NULL;
peOperation=NULL;
bInitResult=FALSE;
nComponent=0;
}
BOOLEAN InitResult(sList *p); //Заполнение списка
void ShowResult(CClientDC* p,COLORREF c);
void ShowResult(CClientDC* pDC,COLORREF cl,int nWidthPen);
void FreeResult(); //Освлбождение списка
void PlusVectorResult(int dx,int dy); //Параллельный перенос списка полигонов
void SetAllbUsedFalse();
void SetAllbUsedTrue();
BOOLEAN BelongResult(CPoint point); //Принадлежность списку
void AddPolygon(sList *pL,int type); //Добавить полигон в список
BOOLEAN ThereIsHole(); //Есть дырки в списке или нет
BOOLEAN DeleteHole(sOperationPolygon *p); //Удалить дырку
BOOLEAN DeletePolygon(sOperationPolygon *pt); //Удалить полигон из списка
BOOLEAN GetbInitResult() {return bInitResult;}
sOperationPolygon *GetpfOperation()
{return pfOperation;}
sOperationPolygon *GetpeOperation()
{return peOperation;}
int GetnComponent() {return nComponent;}
};
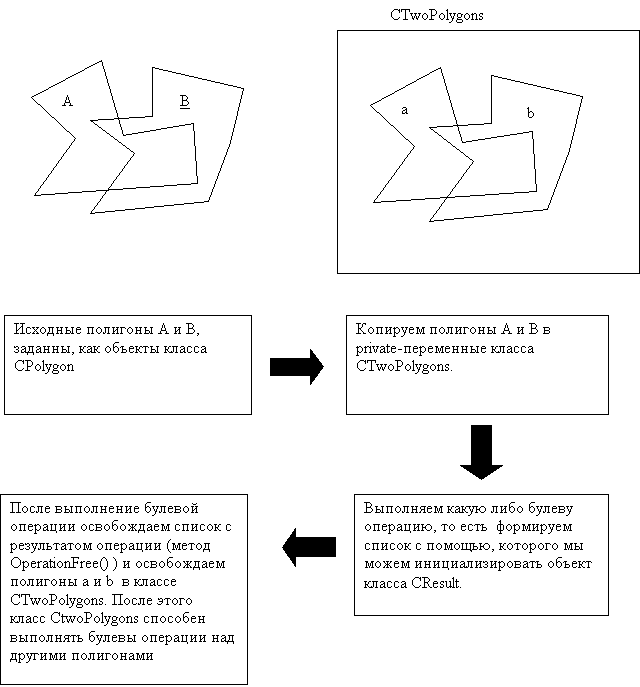
Дальнейшая схема действий приведена на рисунке 5.
|
| Рис. 5 |
Поиск точек пересечения
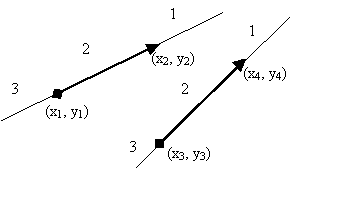
Метод поиска точек пересечения двух выпуклых полигонов подробно описан в работе "Вычислительная геометрия" Препарата, Шеймос. Здесь мы лишь вкратце напомним его. Положение двух ребер пересекаемых полигонов, описывается одной из шести (с точностью до перестановки) ситуаций. (рис. 6)
|
| Рис. 6 |
Пусть прямые порожденные ребрами полигона заданы в параметрическом виде:
X=x1+l*t; Y= y1+m*t; X=x3+p*s; Y= y3+q*s;
Где l= x2 -x1, m= y2 -y1, p= x4 -x3, q= y4 -y3.
Ребра пересекаются тогда, и только тогда, когда t,s содержатся в отрезке [0,1). Это ситуация (2, 2). Основная идея метода основана на разумном продвижении по ребрам полигона. Для создания механизма продвижения по границам необходимо рассмотреть каждый случай в отдельности. Следует двигаться по тому полигону, чья граница в данный момент не может принадлежать пересечению. Следуя этому методу за 2*(L+M) шагов мы найдем все точки пересечения. (Верно ли, что, если за L+M шагов мы не нашли ни одной точки пересечения, то их нет вообще?). Найденные точки пересечения мы загоняем в структуру sCutList.
struct sCutList
{
CPoint cutPoint;
double z; //Координата z векторного произведения ребра первого полигона на ребро
// второго полигона
double ta,tb; // параметры t,s (См. выше)
sList *paCutList; // Указатель на ребро
sList *pbCutList; // Указатель на ребро
sCutList *pCutList; // Указатель на следующую точку пересечения
sCutList *prevCutList; // Указатель на предыдущую точку пересечения
};
Далее, чтобы корректно вставить точки пересечения в полигон, необходимо должным образом их упорядочить. Выбираем первое ребро первого полигона и ищем точки пересечения соотвествующие этому ребру (переменная *paCutList), упорядочиваем их по параметру ta и затем вставляем в полигон. Вставка в динамичекую структуру данных выполняется за костантное время (?). Выполняем аналогичную процедуру для других ребер полигона. Аналогично поступаем и со вторым полигоном.
Описанные выше действия - поиск точек пересечения и вставку их в полигон выполняет метод класса CТwoPolygons InsertCutPoint(). Он возвращает число точек пересечения. Дальнейшие усилия будут направленны на непосредственное формирование списков с результатами булевых операций.
Пересечение полигонов
Пусть переменные класса CTwoPolygons: a, b уже содержат копии исходных полигонов.
Постановка задачи: Сформировать объект класса CResult I такой, что для всех x из того что x содержиться в I следует, что x содержится в a и x содержится в b.
Устанавливаем правую ориентацию полигонов. Вызываем метод N=InsertCutPoint(). Если N=0, то проверяем включения a в b, и b в а. Если ни одно из включений не выполнилось то возвращаем Null и выходим. Если выполнилось первое включение, то заполяем список вершинами полигона а, если второе вершинами полигона b.
Пусть N не равно 0.
1. В полигоне а находим вставленную вершину (у вставленных вершин bTop=FALSE) со значением z<0. Вставляем ее в список. Указателю pFirst присваиваем адрес этой вершины. Организум цикл while ( текущий указатель !=pFirst)
2. Организум цикл while (текущий указатель имеет bTop=TRUE). Заполняем список точками полигона а, до тех пор пока не наткнемся на вставленную вершину. Это означает, что пора переключиться на другой полигон.
3. Ищем во втором полигоне такую же вершину и снова запускаем цикл while (текущий указатель имеет bTop=TRUE).
4. Удаляем из полигонов вставленные вершины.
В результате будет сформирован список содержащий пересечение данных полигонов. В данном алгоритме мы использовали тот факт, что пересечение выпулых полигонов либо пусто либо односвязно.
Разность полигонов.
Разность выпуклых полигонов уже не может быть выпуклым полигоном, кроме того может расподаться на несколько полигонов и иметь дыры.
Постановка задачи: Сформировать объект класса CResult Т такой, что если x содержится в Т, то x содержится в a и x не содержится в b.
Устанавливаем правую ориентацию полигонов. Вызываем метод N=InsertCutPoint(). Если N=0, проверяем включения a в b, b в a. Если выполнилось первое включение возвращаем Null и уходим. Если выполнняется второе включение, заполняем список сначала вершинами полигона а, затем вершинами полигона b и уходим. Если ни одно из включений не выполнилось заполняем список вершинами полигона а и уходим.
Пусть N не равно 0.
1. Организуем цикл while (N)
2. В полигоне а находим вставленную вершину со значением z>0. N=N-1. Вставляем ее в список. Указателю pFirst присваиваем адрес этой вершины. Организум цикл while (текущий указатель !=pFirst)
3. Организум цикл while (текущий указатель имеет bTop=TRUE). Заполяем список точками полигона а, до тех пор пока не наткнемся на вставленную вершину. Это означает, что пора переключиться на другой полигон. N=N-1.
4. Ищем во втором полигоне такую же вершину и снова запускаем цикл while (текущий указатель имеет bTop=TRUE). Но по полигону b движемся в противоположном направлении.
5. Удаляем из полигонов вставленные вершины.
В итоге получим список, с помощью которого мы инициализируем объект класса CResult. Полученный список полигонов будет содержать искомую разность.
Объединение полигонов.
Постановка задачи: Сформировать объект класса CResult W такой, что если x содержится в W, то x содержится в a или x содержится в b.
Устанавливаем правую ориентацию полигонов. Вызываем метод N=InsertCutPoint(). Если N=0, проверяем включения проверяем включения a в b, b в a. Если выполнилось первое включение возвращаем список вершин полигона b, если второе список вершин полигона а. Если данные включения не выполняются, последовательно заполняем список вершинами полигонов a и b.
Пусть N не равно 0.
1. В полигоне а находим вставленную вершину со значением z>0. Вставляем ее в список. Указателю pFirst присваиваем адрес этой вершины. Организум цикл while ( текущий указатель !=pFirst)
2. Организум цикл while (текущий указатель имеет bTop=TRUE). Заполяем список точками полигона а, до тех пор пока не наткнемся на вставленную вершину. Это означает, что пора переключиться на другой полигон.
3. Ищем во втором полигоне такую же вершину и снова запускаем цикл while (текущий указатель имеет bTop=TRUE).
4. Удаляем из полигонов вставленные вершины.
В итоге будет сформирован список с искомым объединением.
Оценка сложности.
Для реализации любой булевой операции, в общем случае, достаточно 2*(L+M)+3*(L+M) шагов. 2*(L+M) шагов - чтобы найти точки пересечения и 3*(L+M) шагов - чтобы сформировать результат и вставить (удалить) точки пересечения. В случае, если ребра полигонов не пересекаются, через L+M шагов мы сумеем установить этот факт. L+M шагов требуется, чтобы проверить два включения. Таким образом, трудоемкость построения алгебры выпуклых полигонов оценивается следующим образом: 2*(L+M) ≤ T(L, M)≤ 5*(L+M)
Бочканов Сергей, Быстрицкий Владимир
Copyright © 1999-2004
При поддержке проекта MANUAL.RU