Алгоритмы перебора
И.И.Данилина
Задачи, разобранные в тексте и предложенные в качестве упражнений,
неоднократно предлагались в разные годы на различных олимпиадах и конкурсах, и
установить их авторов не представляется возможным. В этой серии статей
рассматривается класс алгоритмов реализующих перебор ситуаций. Такие
алгоритмы используются в самых разнообразных задачах — от игр до
проектирования печатных плат. В задачах такого рода часто приходится
вести поиск среди множества объектов (позиций, ситуаций), которые заданы не
сразу все (актуально), а неким правилом, их порождающим (потенциально). В
общем случае для поиска нужного объекта требуется рассмотреть все
возможные объекты, что в связи с большим числом и трудностью их получения
требует слишком большого времени и ресурсов. Однако в ряде случаев
удается не рассматривать заведомо неподходящие объекты. В таких задачах
большую роль играют как выбор модели, так и структура данных.
1. Волновой алгоритм
Для иллюстрации идеи рассмотрим задачу поиска по карте местности
кратчайшего маршрута, соединяющего две заданные точки ("компьютерный штурман").
Если бы все участки были проходимы, то оптимальный маршрут строился бы легко —
это отрезок прямой, соединяющий указанные точки. К сожалению, в жизни имеется
множество непреодолимых для выбранного способа передвижения (например, пешком)
преград (чащи, болота, строения и т.п.). Поэтому задача о выборе оптимального
маршрута не столь проста. Более того, она существенно зависит от того, кто ее
решает. Если решающий — человек, то, выбирая маршрут, он может обозревать карту
местности всю целиком (говорят еще, что человек обладает интегральным
зрением). Компьютеру же для анализа в каждый конкретный момент доступен лишь
некий элемент карты (у компьютера — локальное зрение). В этом различии
между интегральным и локальным зрением и кроется одна из причин затруднения, а
иногда и невозможности переформулирования алгоритма, используемого человеком, в
компьютерный алгоритм.
Прежде всего построим модель задачи. Здесь мы
должны решить, что означают слова: "карта местности", "непроходимый участок",
"кратчайший маршрут".
Одна из возможных моделей такова; карта
местности разбивается на мелкие квадраты, размером которых можно пренебречь, и
координаты точки пересечения диагоналей квадрата примем за координаты этого
квадрата. Тогда всю карту можно представить в виде двухмерного целочисленного
массива Map, индексы которого — координаты соответствующих точек, а
значения — признак возможности прохождения точки с координатами х и у.
Map [х, у] = 0, если участок проходим, и равно —1, если нет. Две точки будем
называть соседними, если они имеют только одну различную координату (например,
точки Map [5, 4] и Map [6, 4] — соседние, а точки Map [5,
4] и Map [6, 3] — нет). Маршрутом будем считать последовательность
соседних точек карты. Длиной маршрута будем считать число клеток в нем (это
определение соответствует случаю равнинной местности, когда при преодолении
любого квадрата проходится примерно одинаковый путь).
В терминах этой
модели исходная задача формулируется так: даны двухмерный числовой массив
Map с элементами, равными 0 и —1, и две пары индексов (две точки):
x_begin, y_begin и x_end, y_end. Требуется построить
последовательность соседних элементов с нулевыми значениями такую, чтобы первым
элементом в ней был Map [x_begin, y_begin] , а последним —
Map [x_end, y_end], причем число элементов в ней было бы
минимальным из всех возможных.
Таким образом, объектами перебора
являются все маршруты, соединяющие указанные точки. Эти маршруты, во-первых,
надо построить (они заданы лишь потенциально), что само по себе непросто,
во-вторых, их может быть очень много (существенно больше, чем число точек на
карте), и из множества построенных маршрутов выбрать маршрут минимальной
длины.
Волновой алгоритм позволяет обойти эти трудности путем
построения сразу оптимального маршрута. При этом, если поставленная задача
неразрешима (нет ни одного маршрута, соединяющего указанные точки), то это
становится известно на некотором этапе. Основная часть этого алгоритма —
построение множества точек, до которых можно добраться за К шагов и
нельзя быстрее (этот процесс аналогичен процессу распространения волны, откуда и
произошло название алгоритма).
Содержательное описание волнового
алгоритма таково:
1. Начальный этап. Пометим начальную
точку числом 1 (в эту точку ведет маршрут длины 0).
2.
Распространение волны. Если рассматриваемая точка помечена числом
К > 0 (в нее можно попасть за К—1 шагов), то все соседние
точки, помеченные нулем, надо пометить числом К + 1 (в них можно попасть за
К шагов). Распространение волны осуществляется до тех пор, пока это
возможно (есть еще соседние, помеченные нулем, точки) и целесообразно (еще не
дошли до конечной точки).
3. Проверка возможности построения
пути. Если после распространения волны конечная точка помечена некоторым
числом К > 0, то в нее можно попасть за К— 1 шаг. В противном случае
эта точка недостижима из начальной.
4. Построение
пути. Для того чтобы построить оптимальный маршрут, необходимо,
начиная с конечной точки, выбирать соседнюю с ней, помеченную числом на единицу
меньше. Затем проделать это же с новой точкой. И так далее, пока не доберемся до
начальной.
Из описания алгоритма видно, что он распадается на два
этапа: распространение волны (включая начальный этап) и построение пути. Такая
структура позволяет естественным образом разбить исходный алгоритм на две
процедуры.
Прежде чем приступить к реализации этих процедур, отметим,
что в них нам придется просматривать точки, соседние с заданной. И здесь нас
подстерегает одна техническая трудность: не у всех точек одинаковое число
соседей — у точек на границе карты соседей меньше. Чтобы избежать лишних
проверок, расширим массив Map и пометим всю границу как непроходимые точки.
Тогда все рассматриваемые точки будут не на границе и поэтому будут иметь
одинаковое число соседей — 4.
Начнем с процедуры распространения
волны. Основное действие — построение очередного фронта волны. Действие нужно
повторить, если очередной фронт волны был построен и до конечной точки еще не
дошли. Процесс построения фронта — просмотр в цикле элементов двухмерного
массива. Таким образом, в реализации построения фронта волны будем использовать
двойной цикл, а процедура распространения волны содержит тройной цикл.
Procedure Wave (x_begin, y_begin, x_end, y_end :
integer);
{ координаты начала и конца пути )
var
k : integer; { номер "фронта волны"
}
х, у : integer; { координаты текущей точки
}
flag : boolean; { признак необходимости строить
очередной фронт }
begin
Map[x_begin, y_begin] := 1; { начальный этап
}
k := 1; (в точку, помеченную
числом k, можно попасть за k-1 шаг
}
flag := true; { нужно строить
фронт }
while flag do { строим
очередной фронт }
begin
flag :=
false;
{ возможно, что волне продвинуться не удастся
}
for х := 1 to Length_Map do { Length_Map - максимальное значение индекса
х}
for у := 1 to Width_Map do { Width_Map - максимальное значение индекса
у}
if Map [х, у] = k
then
begin
{ просмотреть -соседей и пометить очередной
фронт)
if Мар [х+1, у] = 0
then
begin
Мар [х+1, у] := k+1; flag :=
true
end;
if Map [x, y-l] = 0
then
begin
Map [x, y-l] := k+1; flag :=
true
end;
if Map [x, y+l] = 0
then
begin
Map [x, y+l] := k+1; flag :=
true
end;
if Map [x-l, y] = 0
then
begin
Map [x-l, y] := k+1; flag :=
true
end;
end;
if Map[x_end, y_end] > 0 then flag := false
else k :=
k+1
{ переходим к следующему фронту
волны}
end
end;
Процедура формирования пути использует заполненный массив Map и
формирует на его основе массив Way,. начиная от конечной точки.
Procedure Track (x_end, у_end : integer); { построение
пути''}
var
k :
integer; { номер фронта волны
}
step : integer; { номер шага пути
}
х, у : integer; { координаты текущей
точки }
Procedure Way_Step; { присоединение очередной точки к
маршруту}
begin
Way [step, 1] := x; Way [step, 2]
:= у;
step := step+1; k := k-1 { метка следующей
точки }
end;
begin
step :=
1
Way [l, l] := x_end; Way[l, 2] :=
y_end;
k := Map [x_end, y_end] - 1; {
число, которым должна быть помечена следующая точка
}
х := x_end; у :=
у_end;
while k > 0 do { найти
следующую точку }
begin
if Map [x+l, y] =
k
then begin x := x+1; Way_Step
end
else if Map [x, y-l] =
k
then begin у := y-l; Way_Step
end
else if Map [x, y+1] =
k
then begin у := y+1; Way_Step
end
else if Map [x-l, y] =
k
then begin x := x-l; Way_Step end
end
end;
Доказательство оптимальности построенного маршрута достаточно простое. Его
можно предложить школьникам в качестве самостоятельного задания.
Теперь программа, решающая исходную задачу, будет выглядеть следующим
образом:
Program Short_Way;
const Length_Map = 10; Width_Map = 8; {размеры карты
}
var
x_begin, y_begin, x_end, y_end :
integer;
(начало и конец пути }
Map
: array [0..Length_Map+l, 0..Width_Map+l] of integer;
{
карта с добавленными границами }
Way : array
[1..Length_Map * Width_Map,1.. 2] of integer;
{ маршрут
}
i, j, k : integer;
{ описание процедур приведено
выше}
begin
{ перед началом нужно задать
концы маршрута и карту }
Wave (x_begin,
y_begin, x_end, y_end); { волна }
if Map
[x_end, y_end] > 0 { если до конечной точки можно добраться
}
then Track (x_end, y_end) { координаты
точек пути в массиве Way }
else writeln
( ' Маршрут непроходим! ' )
end.
Отметим в заключение, что если бы нас интересовал не сам путь, а лишь
его существование, то ответ на этот вопрос давал бы процесс распространения
волны. В этом случае можно было бы все доступные точки помечать одним и тем же
числом, и сам процесс геометрически означал бы постепенную закраску ограниченной
области. При этом процесс закраски можно ускорить, помечая вместе с соседней
точкой весь луч до границы области.
Упражнение
На шахматной доске расположены белый король и N черных пешек.
Король может брать пешки и ходить по обычным шахматным правилам (т.е. не вставая
на битое поле). Пешки, в отличие от обычной шахматной игры, не могут
перемещаться по доске. Напишите программу, определяющую, может ли король с
заданного поля попасть на другое заданное поле.
2. Волна на графе
Вновь рассмотрим задачу нахождения оптимального
маршрута из одного населенного пункта в другой, но при других
предположениях.
Чтобы достигнуть конечного пункта быстрее, будем
использовать самолет, а следовательно, строить авиационный маршрут. А поскольку
самое неприятное в полете — это взлет и посадка, будем минимизировать их число.
Таким образом, маршрут — это последовательность населенных пунктов А1, А2, ...,
Аn, таких что из Аk в Ak+1 можно долететь без
промежуточных посадок. Мы имеем набор точек, ряд из которых являются "соседними"
(в смысле беспосадочного перелета). Но в отличие от предыдущего случая, когда
каждая точка имела ровно четырех соседей, здесь число соседей может быть
различным у разных точек. Поэтому представить их массивом, аналогично массиву
Map, нам не удастся.
Задачи обработки некоторого набора
объектов, относительно любой пары которых можно сказать, находятся они в
некотором отношении друг к другу ( "соседи") или нет, встречаются довольно
часто. Такие структуры носят специальное название — графы, при этом
сами объекты (точки) называются вершинами, а пары вершин, непосредственно
связанных между собой (соседние), — ребрами.
Маршрутом на графе
называется последовательность вершин A1, А2 ..., Аn такая, что для всех
k = 1,..., n—1 вершины Аk и Аk+1 связаны
ребром.
В этих терминах рассматриваемая задача об авиационном маршруте
формулируется так: задан граф, в котором выделены две вершины, требуется найти
маршрут, соединяющий их и содержащий наименьшее число вершин.
К поиску
маршрута на графе приводят и задачи "трассировки печатных плат" — соединение
радиодеталей (здесь вершины — точки на плате, между которыми можно проводить
соединения, а ребра — возможные пути проведения), и задачи поиска выигрышных
стратегий в играх (здесь вершины — это всевозможные позиции или ситуации,
которые возникают в игре, а ребра — это соседние позиции, то есть такие, что
одна переходит в другую после очередного хода), и многие другие.
При
изображении графа его вершины обозначаются точками, а ребра — отрезками или
линиями, соединяющими вершины. Например, граф с пятью вершинами a, b, с, d,
e и ребрами (a, b), (a, c), (b, c), (с, d) и (d, е) можно изображать
так:
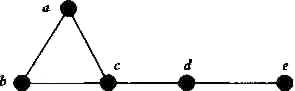
Рис. 1
Простейшим способом описания графа, содержащего п вершин,
является таблица смежности размера n х n. Она строится так:
вершины графа перенумеровываются, и на пересечении i-й строки с
j-й столбцом записывается 1, если вершины с номерами i и j
связаны между собой ребром, и 0 в противном случае. Так, таблица смежности для
графа, изображенного на рис. 1 с нумерацией вершин в алфавитном порядке,
имеет вид:
0 1 1 0 0
1 0 1
0 0
1 1 0 1 0
0 0 1
0 1
0 0 0 1 0
При таком способе описания информацию о графе удобно хранить в
двухмерном числовом массиве с числом строк и столбцов, равным числу вершин
(таблица смежности).
К сожалению, таблица смежности неэкономна, так
как в ней содержится избыточная информация, в то время как для работы с графом
достаточно перечислить лишь соседние пары (которых может быть существенно
меньше, чем всех пар).
Другим способом представления графов (и часто
более экономичным) являются списковые структуры, в которых ссылки указывают на
соседние вершины. Например, для графа, изображенного на рис. 1, списковую
структуру можно взять такую, как на рис. 2.
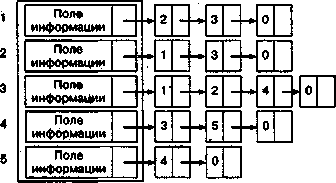
Массив записей;
каждый элемент
массива
содержит
имя вершины (номер) и указатель на список соседних с ней
вершин. Этот массив создается статически (перед началом работы
программы) |
Списки создаются динамически в процессе работы
программы |
Рис. 2
Ниже приведены описание данных и процедура создания списковой
структуры для представления графа:
{ . . . }
const max_graf = 100; {
максимальное число вершин
графа}
type list =
^elem;
elem =
record
num :
integer;
next :
list;
end;
var
Graf : array[1..max_graf] of elem;
{ . . . }
Procedure
CreateGraf(n:integer) ;
(n - число вершин графа)
var
a:integer;
sosed,sosed1 :
list;
begin
for i:=1 to n do { для каждой вершины
}
begin
new(sosed); {
выделили память для нового элемента
}
graf[i].next :=
sosed; { ссылка на новый элемент
}
Writeln ('Для
элемента ' , i , ' введите номер очередного соседа или 0 ')
;
repeat
Readln(a);
sosed^.num := а; { указатель на очередного соседа
}
if
а<>0
then
begin
new(sosed1);
sosed^. next :=
sosed1
sosed :=
sosed1
end;
until a=0 {
больше соседей нет}
end
end;
Задача поиска кратчайшего маршрута на графе полностью аналогична
рассмотренной ранее задаче поиска на карте (с той только разницей, что нет
вершин, запрещенных для использования, — их можно выбросить на этапе
формализации задачи, так как это в отличие от карты не нарушает общей структуры
рассматриваемых данных). Поэтому для ее решения можно применить волновой
алгоритм.
Покажем, как в этом случае будет выглядеть процедура
распространения волны.
Procedure Wave (num_begin, num_end : integer)
;
{ номера вершин начала и конца пути }
var
k : integer; { номер "фронта
волны" }
num :
integer; { номер текущей вершины }
flag : boolean; { признак необходимости строить очередной фронт
}
beg_qu, end_qu, elem_qu : list;
{ начало,
конец и элемент очереди }
Procedure Add (num : integer; var end_qu : list );
{ добавление элемента к
очереди }
var
elem_qu : list;
begin
end_qu^ .num:=num; {
поместили элемент в конец очереди }
new(elem_qu); {
выделили память под следующий элемент }
end_qu^.next:=elem_qu; {присоединили новый элемент }
end qu:=elem_qu
end;
Procedure Extract (var num : integer; var begin_qu : list );
{ извлечь
элемент из списка }
var
elem_qu :
list;
begin
num:=beg_qu^.num; { считали первый
элемент очереди }
elem_qu:=beg_qu; { запомнили
ссылку на первый элемент для последующего уничтожения
}
beg_qu:=beg_qu^.next; { переносим указатель начала
очереди на второй элемент}
Dispose(elem_qu) {
освобождаем память, уничтожив первый элемент
}
end;
begin
new(elem_qu);{ инициализация
очереди и размещение в ней первого элемента }
beg_qu:=elem_qu; { очередь пока пуста }
end_qu:=elem_qu;
Graf [ num_begin] .nurn := 1;
{начальный этап }
Add(num_begin, end_qu); {поместили
начало пути в очередь }
flag := true; {нужно строить
фронт }
while flag and (not goal) do { строим
очередной фронт }
begin
Extract (nurn,
beg_qu) ;
{ берем
значение очередного элемента очереди
}
k:=Graf[num].num; {
число шагов до извлеченного элемента — 1
}
{ просмотреть
соседей, пометить очередной фронт и добавить помеченные элементы в очередь
}
ref :=
graf[num].next
repeat
а:=геf^.num;
if a<>0 then
begin
{обработка очередного
соседа}
if
Graf[a].num=0
{пометить вершину следующим
фронтом}
then
begin
Graf[a].num:=
k+1;
Add(a,end_qu)
end;
ref :=
ref^.next
{ переходим к следующему соседу
}
end
until
a=0;
if Graf[num_end]
.num<>0
then goal:=true { дошли до цели
}
else
if beg_qu=end_qu then flag:=false {очередь пуста }
end
end;
Упражнение
Имеется механизм, состоящий из N расположенных в одной плоскости и
свободно надетых на зафиксированные оси пронумерованных шестеренок, зубья
которых сопрягаются друг с другом. Информация о механизме ограничивается
тем, что для каждой шестеренки перечислены все те, с которыми она находится
в непосредственном зацеплении. Напишите программу, определяющую, есть ли
такая шестеренка, поворачивая которую мы приведем в движение весь
механизм.
3. Бектрекинг на графе, заданном перечислением вершин и
ребер
Рассмотренный ранее волновой алгоритм имеет
существенный недостаток. Он требует хранения меток (номера волновых фронтов)
всех вершин, до которых докатилась волна (в самом худшем случае это будут все
вершины графа). Во-первых, при большом числе вершин может просто не хватить
памяти. Во-вторых (и это более существенно), мы должны иметь быстрый доступ ко
всем "соседям" очередного волнового фронта. Однако если граф задан
потенциально, то есть некоторым правилом порождения вершин и ребер
(например, граф шахматных позиций), то даже при не очень большом числе вершин
возникает проблема порядка их построения (и просмотра) и необходимых для этого
затрат (времени, памяти). При этом большинство вершин будут с точки зрения
окончательного маршрута построены зря.
Рассмотрим, например, задачу
выхода из произвольного лабиринта. Лабиринт — это система комнат,
некоторые из которых соединены коридорами. С абстрактной точки зрения это,
конечно, граф (вершины — комнаты, ребра — коридоры). Некто, заблудившийся в
лабиринте, желает выйти из него.
Формализация этой задачи внешне
выглядит знакомо: найти маршрут, возможно, и не кратчайший, соединяющий
начальную вершину с конечной. Однако при отсутствии плана лабиринта для
нахождения нужного маршрута заплутавший путник не может применить волновой
алгоритм (нельзя быть уверенным, что, например, пятая комната, в которую путник
попал, начав свой поиск, действительно принадлежит четвертому фронту волны, а не
меньшему — возможно, по другому коридору можно попасть в эту комнату сразу из
первой).
В этом случае поиск можно вести следующим методом (являющимся
с житейской точки зрения методом проб и ошибок).
1. При
продвижении вперед всегда входить в новую комнату, в которую еще не входили (для
определенности можно считать, что эта комната с наименьшим номером из
возможных).
2. Если этого сделать нельзя, то необходимо вернуться
назад (в предыдущую комнату), пометив покинутую комнату как запрещенную для
входа в нее.
На рисунке приведен пример лабиринта, а ниже показан
процесс работы нашего алгоритма для этого лабиринта (определяется путь из
комнаты № 1 в комнату № 16; выписывается пройденный путь, то есть номера комнат,
через которые надо пройти).
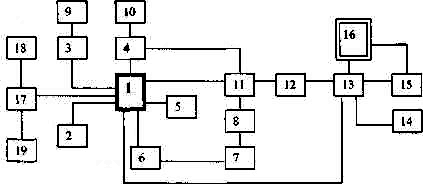
1
1-2 из комнаты № 2 никуда пойти нельзя — это тупик, надо
вернуться;
1
1-3
1-3-9 комната № 9 — тоже тупик, надо вернуться;
1-3
теперь из комнаты № 3 тоже некуда пойти, так как в комнате № 9 мы уже побывали,
снова возвращаемся;
1
1-4
1-4-10 комната № 10 ~ снова
тупик;
1-4
1-4-11
1-4-11-8
1-4-11-8-7 из комнаты № 8 можно идти
только в комнату № 7, так как в комнате № 11 мы уже были:
1-4-11-8-7-6 из
комнаты N' 6 попасть в новую комнату уже нельзя — надо
возвращаться;
1-4-11-8-7
1-4-11-8
1-4-11
1-4-11-12
1-4-11-12-13
1-4-11-12-13-14
комната № 14 -
тупик;
1-4-11-12-13
1-4-11-12-13-15
1-4-11-12-13-15-16
На этом примере мы видим, что формирование пути можно вести с
использованием стека — структуры данных, устроенной так же, как и очередь, с той
лишь разницей, что извлечь (удалить из стека) можно только последний добавленный
элемент. При этом считается, что добавляются и удаляются элементы из вершины
стека. Рассмотренный алгоритм гарантирует, что никогда не получится маршрут,
являющийся продолжением забракованного, с другой стороны, не исключаются из
дальнейшего рассмотрения никакие другие маршруты, кроме уже
забракованных.
Характерная черта метода — возвращение к предыдущей
вершине. Поэтому его называют еще методом поиска с возвратом, или
бектрекингом (back tracking (англ.) — обратное следование).
Отметим, что на каждом шаге алгоритма приходится просматривать соседей лишь
одной вершины и помнить информацию лишь об уже рассмотренных, что существенно
сокращает требуемые ресурсы (в нашем примере вершины с номерами 17, 18 и 19 не
рассматривались совсем).
Однако маршрут, получаемый бектрекингом,
существенно зависит от выбранного порядка просмотра соседей и, вообще говоря, не
самый короткий (в нашем примере кратчайший маршрут: 1—11—12—13—16).
Приступим к реализации бектрекинга в случае поиска маршрута в
лабиринте.
Граф, соответствующий лабиринту, представим списковой
структурой, хранящейся в массиве Graf. В поле Graf [i] , num хранится информация
о том, были мы в комнате i или нет (1 — были, 0 — нет).
После
работы алгоритма массив Graf уже отличается от того, каким он был в начале (как,
впрочем, и лабиринт, если пройденные комнаты помечать мелом или краской).
const max_graf = 100;(максимальное число комнат в лабиринте}
type list
=^elem;
elem =
record
num :
integer;
next :
list;
end;
var
Graf: array [1. . rnax_graf] of elem;
ref:
list;
n, i, a :
integer;
goal, go_on : boolean;
{признаки достижения цели и необходимости
продолжения}
beg_num,end_num :
integer;
beg_st, end_st, elem_st : list; {
начало, конец и элемент стека }
. . .
Procedure
CreateGraf(n:integer);
{чтение исходных данных из текстового файла и
формирование графа}
var
sosed,
sosed1 : list;
begin
for i:=l
to n do
begin
new(sosed);
graf[i].next :=
sosed;
repeat
Readln(inf,a)
;
sosed^.num :=
a;
if а<>0
then
begin
new(sosed1);
sosed^.next :=
sosed1;
sosed :=
sosed1
end
until a=0
end
end;
Формирование маршрута ведется с использованием стека. Процедуры Add и
Del предназначены соответственно для добавления и удаления элементов стека.
Procedure Add (num: integer; var beg_st : list );
{ добавление элемента к
стеку }
var
elem_st
: list;
begin
new(elem_st); { выделили память под следующий элемент
стека}
elem_st^.next:=beg_st; {присоединили новый элемент к стеку
}
elem_st^.num:=num; {занесли
информацию)
beg_st:=elem_st {установили указатель на новое начало стека}
end;
Procedure Del (var begin_st : list ) ;
{ удалить элемент из стека
}
var
elem_st :
list;
begin
elem_st:=beg_st;
beg_st:=beg_st^.next; { переносим указатель начала (вершины) стека на второй
элемент}
Dispose(elem_st) {
освобождаем память, уничтожив первый элемент}
end;
Основное действие алгоритма — это обработка очередной вершины графа, в
результате чего мы либо добавляем к маршруту новую вершину, либо возвращаемся в
предыдущую. Порядок просмотра соседей определяется порядком следования
полей-ссылок в перечне вершин-соседей, который соответствует одной записи в
текстовом файле.
Procedure Way (num_begin, num_end : integer); { номера вершин начала и конца
пути }
var
num : integer; { номер текущей
вершины }
flag : boolean; { признак
необходимости продолжения пути }
begin
Graf
[num_begin] .num : = 1; { начальный этап }
Add
(num_begin, beg_st) ; {поместили начало пути в. стек
}
flag := true; {нужно продолжать построение
пути }
while flag and (not goal) do { строим
очередной фронт }
begin
num := beg_st^.num
;
{
берем значение вершины стека
}
ref := graf
[num].next;
go_on :=
false; {признак того, что путь
увеличился}
repeat
a: =ref^
.num;
if а<>0
then
begin
{обработка очередного
соседа}
if Graf[a]. num=0 {пометить вершину следующим
фронтом}
then
begin
Graf [a].num :=
1;
Add(a, beg_st)
;
go_on := true; {путь увеличился на
шаг}
end
else
ref := ref^.next { переходим к следующему соседу
}
end;
until
(a=0) or
(go_on);
if Graf [num_end].num<>0 then goal :=true { дошли до цели.
}
else
if not go_on
then
begin
del (beg_st)
;
if beg_st=end_st then
flag:=false
{ стек пуст, задача неразрешима
}
end
end
end;
Теперь программу поиска маршрута можно записать так (структура графа
считывается из текстового файла):
program BackTracking;
. .
.
begin
for i:=1 to
Max_Graf do Graf [i].num :=0;
assign (inf, 'graf.txt');
{ в
файле приведен пример, разобранный в тексте
(рис.3)}
reset
(inf);
readln (inf,n); { число
вершин графа }
CreateGraf (n)
;
close (inf)
;
new (elem_st) ; { инициализация
стека }
beg_st:=elem_st; { стек
пока пуст,}
end_st:=elem_st; {
призак этого: beg_st = end_st}
goal := false;
Writeln;
Writeln('Введите номер
начальной и конечной вершины'};
Readln (beg_num, end_num) ;
Way
(beg_num, end_num) ;
if goal
then
{
построение и печать маршрута }
. .
.
end.
Упражнение
Напишите процедуру
построения и печати пути по лабиринту.
4. Алгоритм бектрекинга на потенциально заданном
графе
Проницательный читатель, вполне возможно, остался
не удовлетворен решением задачи о выходе из лабиринта. И причина этого в
несоответствии идеи алгоритма и формы представления данных. Поиск ведется в
предположении, что граф задан потенциально (путник не имеет плана, а видит лишь
данную вершину и может попасть в соседнюю, "построив" ее), а форма представления
соответствует актуально заданному графу (в массиве Graf хранится
информация обо всех вершинах). То есть в данном случае компьютер
выступает в роли "высшего существа", которому известно все, но который прячет
часть информации от управляемого им путника.
Авторы пошли на это
сознательно, чтобы продемонстрировать идею метода в чистом виде, не осложняя ее
новыми проблемами представления исходных данных. Теперь, когда, надеемся, сам
метод бектрекинга понятен, можно переходить и к общему случаю.
Рассмотрим такую задачу: заданы к конвертов с размерами Аi X Вi и
k прямоугольных открыток с размерами Сi х Di. Написать алгоритм для
раскладки (если это возможно) открыток по конвертам.
Если бы открытки
и конверты можно было упорядочить таким образом, что если какая-то открытка
помещается в данный конверт, то в этот конверт помещается и любая другая
открытка с меньшими размерами (и, соответственно, рассматриваемая открытка
помещается в любой конверт с большими размерами), то задача решалась бы легко.
После такого упорядочения мы получили бы соответствие между конвертами и
открытками, которое либо удовлетворяет условиям, либо задача неразрешима. Это
можно было бы сделать, если бы открытки и конверты были стандартными, в том
смысле, что отношение размеров (А:В к C:D) было бы постоянным. Однако в нашем
случае это не так.
Попытка решить эту задачу простым перебором,
последовательно формируя всевозможные перестановки из к чисел (этих
перестановок к! = 1 • 2 • 3 • ... • k) и проверяя, подходят ли они
нам (проверка — цикл, повторяющийся еще k раз), дает алгоритм, который
работает очень долго.
Другой подход связан с постепенным наращиванием
искомой последовательности. А именно, если нам уже удалось заполнить первые
n конвертов открытками, то на следующем шаге надо попытаться заполнить
еще один конверт, т.е. увеличить последовательность на одно число. Либо, если
этого сделать нельзя, освободить последний конверт, т.е. уменьшить исходную
последовательность на одно число, так как этот вариант "тупиковый". После чего
повторять все сначала. Таким образом, мы не будем рассматривать все варианты,
начинающиеся с тупиковой последовательности. И если эта последовательность
коротка, например длины 1, то нам удастся отбросить много заведомо неподходящих
последовательностей. Можно заметить, что процесс построения итоговой
последовательности подобен процессу построения маршрута выхода из лабиринта, то
есть бектрекингу.
Займемся реализацией алгоритма для данного
случая.
Исходную информацию удобно хранить в двух массивах —
Env и Card.
program Envelopes;
const max = 100; {ограничение на число конвертов и
открыток}
var
inf:text; {файл с
исходными данными }
Card :
array[1..max] of {
открытки}
record
length : integer; { длина
}
width : integer; { ширина
}
In_E : boolean { открытка в конверте или нет
}
end;
Env : array[1..max] of {
конверты
)
record
length : integer; { длина
}
width : integer; { ширина
}
N_card : integer { номер открытки в этом конверте
}
end;
n, i :
integer;
N_card, NC, NC1, N_env :
integer;
flag : boolean; {признак
необходимости продолжать процесс }
Отметим особо, что в силу специфики задачи мы не можем прийти к одной
и той же последовательности конвертов (вершине) различными путями. Поэтому нет
необходимости запоминать все уже просмотренные ранее ситуации, а надо лишь
обеспечить выбор действительно нового соседа. При этом поиск связан с перебором
открыток, еще не помещенных в конверт. Чтобы отличить "свободные" открытки от
уже размещенных, используется поле In_E в каждой открытке.
Ввод исходных данных удобно организовать из файла:
Procedure Input;
{ ввод данные из файла Env.txt
}
var
i :
integer;
begin
assign (inf, '
env_car,. txt' );
reset (inf)
;
readln (inf, n); { число
конвертов }
for i:=1 to n
do
begin
Readln (inf, Env[i] . length, Env[i] . width); Env[i] .
N_card:=0
end;
for i :=1 to n
do
begin
Readln (inf ,Card[i] . length, Card.[i] .width) ; Card[i] .
In_E:=false
end;
close(inf)
end;
Проверку соответствия открытки конверту удобно оформить в виде
логической функции
Function Voidet (a, b, с,
d:integer):boolean;
begin
Voidet:=(a>c) and (b>d) or (a>d) and (b>c)
end;
Основной шаг алгоритма — обработка последовательности конвертов
(вершины графа), в результате чего либо эта последовательность увеличивается на
единицу, либо уменьшается на единицу. При этом, чтобы обеспечить рассмотрение
нового "соседа", необходимо начинать просмотр по-разному, в зависимости от того,
что было сделано на предыдущем шаге, — продвижение вперед или назад. В первом
случае все свободные в данный момент открытки являются претендентами на
помещение в очередной конверт. Во втором случае рассматриваются лишь те
открытки, которые еще в этот конверт не помещались. Для этого введем N_card
— наименьший номер открытки, начиная с которого ведется поиск. Тогда,
выбирая на каждом шаге подходящий конверт с наименьшим номером, мы получим
следующее правило определения N_card: после продвижения вперед
N_card должно быть равно 1, а после возвращения назад — на 1 больше
номера неподошедшей открытки.
Итак, алгоритм в окончательном виде
выглядит следующим образом:
begin
N_env := 1; { текущий
номер конверта }
N_card :=1; {
наименьший номер открытки — претендента на текущий
конверт}
flag := true; { нужно
продолжать процесс раскладки }
while flag do
begin
NC := N_card; {
номер текущей открытки
}
NC1 :=
0; { номер положенной открытки
}
While NC
<= n do
begin
if not Card[NC],In_E then { открытка NC свободна
}
begin
if Voidet(Env[N_env] . length, Env[N_env] . width, Card[NC] . length,
Card[NC].width)
then { открытку положили, из цикла вышли
}
begin NC1 := NC; NC := n+1
end
end;
NC := NC+1 { перейти к следующей открытке
}
end;
if NC1 > 0 then { открытка NC может быть положена в конверт N_env
}
begin Env [N_env] . N_card :=
NC1;
if N_env =
n
then flag
:=.false
else
begin
N_env := N_env +
1;
Card[MC1].In_e :=
true;
N_card :=
1
end
end
else { в текущий конверт ничего положить нельзя
}
if N_env = 1
then
begin
writeln ('Задача
неразрешима');
flag :=
false;
end
else
begin
N_card := Env[N_env-l] . N_card
+1;
{ мин. номер открытки, которую еще не пытались вложить в предыдущий
конверт}
N_env := N_env -
1;
Card[N_card - l] . In_e :=
false
end
end;
if N_env = n then (все
открытки удалось разложить по
конвертам}
for i := 1 to n do write (Env[i].N_card,' '); { номера открыток в конвертах
}
else write ('Задача
неразрешима');
writein
end.
Упражнение
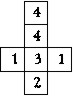
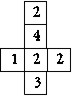
Напишите программу для решения головоломки "Американские
кубики". Даны четыре кубика — на рисунке изображены их развертки.
Нужно сложить из них башню 1 х 1 х 4, чтобы на каждой боковой грани встречались
все четыре
цифры.
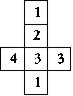

Идеи
алгоритмов заимствованы из следующих источников:
1. Абрамов
С.А. Математические построения и программирование. М.: Наука, 1978. С.
192.
2. Липский В. Комбинаторика для программистов.
М.: Мир, 1988. С. 213.
3. Холл П. Вычислительные структуры.
Введение в нечисленное программирование. М.: Мир, 1978. С. 214.







