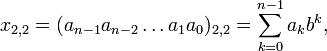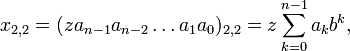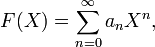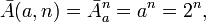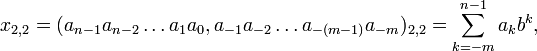Двоичная система счисления

Системы счисления в культуре
Индо-арабская система счисления
Арабская Индийские Тамильская Бирманская	Кхмерская Лаоская Монгольская Тайская
Восточноазиатские системы счисления
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные системы счисления
Абджадия Армянская Ариабхата Кириллическая	Греческая Эфиопская Еврейская
Другие системы
Вавилонская Египетская Этруская Римская	Аттическая Кипу Майская
Позиционные системы счисления
Десятичная система счисления (10)
2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 60
Нега-позиционная система счисления
Непозиционные системы счисления
Единичная (унарная) система счисления
Список систем счисления

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).

История

• Полный набор из 8 триграмм и 64 гексаграмм, аналог 3-битных и 6-битных цифр, был известен в древнем Китае в классических текстах книги Перемен. Порядок гексаграмм в книге Перемен, расположенных в соответствии со значениями соответствующих двоичных цифр (от 0 до 63), и метод их получения был разработан китайским учёным и философом Шао Юн в XI веке. Однако нет доказательств, свидетельствующих о том, что Шао Юн понимал правила двоичной арифметики, располагая двухсимвольные кортежи в лексикографическом порядке.

• Индийский математик Пингала (200 год до н. э.) разработал математические основы для описания поэзии с использованием первого известного применения двоичной системы счисления.

• Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы, так и не числовых записей в двоичной системе кодирования. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись.

• Наборы, представляющие собой комбинации двоичных цифр, использовались африканцами в традиционных гаданиях (таких как Ифа) наряду со средневековой геомантией.

• В 1605 году Френсис Бэкон описал систему, буквы алфавита которой могут быть сведены к последовательностям двоичных цифр, которые в свою очередь могут быть закодированы как едва заметные изменения шрифта в любых случайных текстах. Важным шагом в становлении общей теории двоичного кодирования является замечание о том, что указанный метод может быть использован применительно к любым объектам. (См. Шифр Бэкона)

• Современная двоичная система была полностью описана Лейбницем в XVII веке в работе Explication de l’Arithmétique Binaire. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени.

• В 1854 году английский математик Джордж Буль опубликовал знаковую работу, описывающую алгебраические системы применительно к логике, которая в настоящее время известна как Булева алгебра или алгебра логики. Его логическому исчислению было суждено сыграть важную роль в разработке современных цифровых электронных схем.

• В 1937 году Клод Шеннон представил к защите кандидатскую диссертацию Символический анализ релейных и переключательных схем в MIT, в которой булева алгебра и двоичная арифметика были использованы применительно к электронным реле и переключателям. На диссертации Шеннона по существу основана вся современная цифровая техника.

• В ноябре 1937 года Джордж Штибиц, впоследствии работавший в Bell Labs, создал на базе реле компьютер «Model K» (от англ. «Kitchen», кухня, где производилась сборка), который выполнял двоичное сложение. В конце 1938 года Bell Labs развернула исследовательскую программу во главе со Штибицом. Созданный под его руководством компьютер, завершённый 8 января 1940 года, умел выполнять операции с комплексными числами. Во время демонстрации на конференции American Mathematical Society в Дартмутском колледже 11 сентября 1940 года Штибиц продемонстрировал возможность посылки команд удалённому калькулятору комплексных чисел по телефонной линии с использованием телетайпа. Это была первая попытка использования удалённой вычислительной машины посредством телефонной линии. Среди участников конференции, бывших свидетелями демонстрации, были Джон фон Нейман, Джон Мокли и Норберт Винер, впоследствии писавшие об этом в своих мемуарах.

Запись двоичных чисел

Двоичная система счисления является частным случаем сдвоенных двоичных показательных позиционных систем счисления с обоими основаниями (a и b) равными 2. Положительные целые числа (без знака) записываются в виде:

$\ x_{2,2} = (a_{n-1} a_{n-2}\dots a_{1} a_{0})_{2,2} = \sum_{k=0}^{n-1} a_k b^k,$

где:

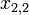• $\ x_{2,2}$ — представляемое число,
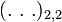• $\ (.\ .\ .)_{2,2}$ — запись числа, строка цифровых знаков,
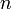• $\ n$ — число цифр (знаков) в числе x_2,2,
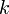• $\ k$ — порядковый номер цифры,
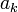• $\ a_k$ — цифры числа x_2,2 из множества a={0,1}, в двоичной системе счисления основание внутриразрядной системы счисления равно 2,
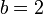• $\ b=2$ — основание показательной весовой функции, основание межразрядной системы счисления,
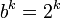• $\ b^k=2^k$ — весовая показательная функция, создающая весовые коэффициенты.

Целые числа со знаком записываются в виде:

$\ x_{2,2} = (za_{n-1} a_{n-2}\dots a_{1} a_{0})_{2,2} = z\sum_{k=0}^{n-1} a_k b^k,$

где:

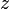• $\ z$ — знак числа из множества z={+,-}, у положительных целых чисел знак зачастую опускается.

Целые числа являются частными суммами степенного ряда:

$F(X) = \sum\limits_{n=0}^{\infty}a_nX^n,$

в котором коэффициенты a_n берутся из кольца R=a{0,1}, X=2, n=k, а верхний предел в частных суммах ограничен с 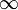$\infty$ до — n-1.

Основание показательной функции — b определяет только диапазон представляемых числами x_2,b величин.
Число записываемых кодов от основания показательной функции - b не зависит.
Число записываемых кодов зависит от основания внутриразрядной системы счисления - a, определяется в комбинаторике и равно числу размещений с повторениями:

$\bar{A}(a,n)=\bar{A}_a^n=a^n=2^n,$

где a=2 — 2-х элементное множество a={0,1} из которого берутся цифры a_k, n — число элементов (цифр) в числе x_2,b.

Дробные числа записываются в виде:

$x_{2,2} = (a_{n-1} a_{n-2}\dots a_{1} a_{0},a_{-1} a_{-2}\dots a_{-(m-1)} a_{-m})_{2,2} = \sum_{k=-m}^{n-1} a_k b^k,$

где:

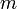• $\ m$ — число цифр дробной части числа,
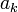• $\ a_k$ — весовые коэффициенты из множества 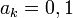$\ a_k={0,1}$, основание внутриразрядной системы счисления равно 2,
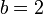• $\ b=2$ — основание показательной весовой функции, основание межразрядной системы счисления.

Следует отметить, что число может быть записано в двоичном виде, а система счисления при этом может быть не двоичной, с другим основанием. Пример: двоично-десятичное кодирование, в котором десятичные цифры записываются в двоичном виде, а система счисления — десятичная.

Сложение, вычитание и умножение двоичных чисел

Таблица сложения

+	0	1
0	0	1
1	1	10

Пример сложения «столбиком» (14 + 5 = 19):

		1	↖
+		1	1	1	0
			1	0	1
	1	0	0	1	1

Таблица вычитания

-	0	1
0	0	1
1	1	0

Таблица умножения

×	0	1
0	0	0
1	0	1

Пример умножения «столбиком» (14 × 5 = 70):

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0

Преобразование чисел

Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:

512

256

128

64

32

16

8

4

2

1

Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1, называется двоичной точкой.

Преобразование двоичных чисел в десятичные

Допустим, вам дано двоичное число 110001. Для перевода в десятичное просто запишите его справа налево как сумму по разрядам следующим образом:

$1\times 2^0 + 0\times 2^1 + 0\times 2^2 + 0\times 2^3 + 1\times 2^4 + 1\times 2^5 = 1\times 1 + 0\times 2 + 0\times 4 + 0\times 8 + 1\times 16 + 1\times 32= 49$.

Можно записать это в виде таблицы следующим образом:

512	256	128	64	32	16	8	4	2	1
				1	1	0	0	0	1
				+32	+16				+1

Точно так же, начиная с двоичной точки, двигайтесь справа налево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа.
Таким образом, двоичное число 110001 равнозначно десятичному 49.

Преобразование методом Горнера

Перевод целых чисел методом Горнера Для того, чтобы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47. Перевод дробных чисел методом Горнера 1) 0,1101₂=0,X₁₀ (рассматриваем цифры в обратном порядке)
1:2=0,5
0,5+0=0,5
0,5:2=0,25
0,25+1=1,25
1,25:2=0,625
0,625+1=1,625
1,625:2=0,8125
Ответ: 0,1101₂= 0,8125₁₀
2) 0,356₈=0,X₁₀ (рассматриваем цифры в обратном порядке)
6:8=0,75
0,75+5=5,75
5,75:8=0,371875
0,371875+3=3,371875
3,371875:8=0,46484375
Ответ: 0,356₈=0,46484375₁₀
3) 0,A6E₁₆=0,X₁₀ (рассматриваем цифры в обратном порядке)
14:16=0,875
0,875+6=6,875
6,875:16=0,4296875
0,4296875+10=10,4296875
10,4296875:16=0,65185546875
Ответ: 0,A6E₁₆=0,65185546875₁₀

Преобразование десятичных чисел в двоичные

Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :

19 /2 = 9  с остатком 1
9  /2 = 4  c остатком 1
4  /2 = 2  без остатка 0
2  /2 = 1  без остатка 0
1  /2 = 0  с остатком 1

Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справа налево. Т.е. нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.

Преобразование дробных двоичных чисел в десятичные

Нужно перевести число 1011010.101 в десятичную систему. Запишем это число следующим образом:

$\begin{align}&1\times 2^6 + 0\times 2^5 + 1\times 2^4 + 1\times 2^3 + 0\times 2^2 + 1\times 2^1 + 0\times 2^0 + 1\times 2^{-1} + 0\times 2^{-2} + 1\times 2^{-3} = \\ &= 1\times 64 + 0\times 32 + 1\times 16 + 1\times 8 + 0\times 4 + 1\times 2 + 0\times 1 + 1\times \frac{1}{2} + 0\times \frac{1}{4} + 1\times \frac{1}{8} = 90,625 \end{align}$

Преобразование дробных десятичных чисел в двоичные

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

• Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
• Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
• В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
• Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0.232
.232 • 2 = 0.464
.464 • 2 = 0.928
.928 • 2 = 1.856
.856 • 2 = 1.712
.712 • 2 = 1.424
.424 • 2 = 0.848
.848 • 2 = 1.696
.696 • 2 = 1.392
.392 • 2 = 0.784
и т. д.
Получим: 206,116₁₀=11001110,0001110110₂

Применения

В цифровых устройствах

Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:

• Чем меньше значений существует в системе, тем проще изготовить отдельные элементы, оперирующие этими значениями. В частности, две цифры двоичной системы счисления могут быть легко представлены многими физическими явлениями: есть ток (ток больше пороговой величины) — нет тока (ток меньше пороговой величины), индукция магнитного поля больше пороговой величины или нет (индукция магнитного поля меньше пороговой величины) и т. д.
• Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать. Например, чтобы закодировать три состояния через величину напряжения, тока или индукции магнитного поля, потребуется ввести два пороговых значения и два компаратора, что не будет способствовать помехоустойчивости и надёжности хранения информации.^{[источник не указан 465 дней]}
• Двоичная арифметика является довольно простой. Простыми являются таблицы сложения и умножения — основных действий над числами.

В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует (очевидно) один двоичный разряд двоичного регистра, то есть двоичный триггер с двумя состояниями (0,1).

В английской системе мер

При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7¹⁵/₁₆″, 3¹¹/₃₂″ и т. д.

См. также

• Битовые операции
• Системы счисления
• Бит
• Байт
• Единицы измерения информации
• Двоичные логические элементы
• Двоичный триггер
• Двоично-десятичный код
• Двоичное кодирование
• Азбука Морзе

Примеры чисел-степеней двойки

Степень	Значение
1	2
2	4
3	8
4	16
5	32
6	64
7	128
8	256
9	512
10	1024
11	2048
12	4096
13	8192
14	16384
15	32768
16	65536
17	131072
18	262144
19	524288
20	1048576
21	2097152
22	4194304
23	8388608
24	16777216
25	33554432
26	67108864
27	134217728
28	268435456
29	536870912
30	1073741824
31	2147483648
32	4294967296
33	8589934592
34	17179869184
35	34359738368
36	68719476736
37	137438953472
38	274877906944
39	549755813888
40	1099511627776
41	2199023255552
42	4398046511104
43	8796093022208
44	17592186044416
45	35184372088832
46	70368744177664
47	140737488355328
48	281474976710656
49	562949953421312
50	1125899906842624

Ссылки

• Учебное пособие «Арифметические основы ЭВМ и систем». Часть 1. Системы счисления
• Hexadecimal Decimal Binary Octal Converter for programmers