Олимпиадные задачи по программированию.

Вычислить значение суммы

S = 1/1! + 1/2! + ... + 1/k!

[Решение]

Написать программу определения количества шестизначных 'счастливых' билетов, у которых сумма первых 3 десятичных цифр равна сумме 3 последних десятичных цифр.

[Решение]

Написать программу определения количества 2*N -значных билетов, у которых сумма первых N десятичных цифр равна сумме N последних десятичных цифр; при этом N -произвольное натуральное число.

[Решение]

Фишка может двигаться по полю длины N только вперед. Длина хода фишки не более K. Найти число различных путей, по которым фишка может пройти поле от начала до конца.

Пример. N=3, K=2

Возможные пути:

1,1,1

1,2

2,1

Ответ: 3.

[Решение]

Покупатель имеет купюры достоинством A(1), ...,A(n), а продавец - B(1), .. ,B(m). Необходимо найти максимальную стоимость товара Р, которую покупатель не может купить, потому что нет возможности точно рассчитаться за этот товар с продавцом, хотя денег на покупку этого товара достаточно.

[Решение]

Задан массив М [1:N] натуральных чисел, упорядоченный по неубыванию, т.е.: M[1]<=M[2]<=...<=M[N].

Найти первое натуральное число, не представимое суммой никаких элементов этого массива, при этом сумма может состоять и из одного слагаемого, но каждый элемент массива может входить в нее только один раз.

[Решение]

У покупателя есть n монет достоинством H(1),..., H(n). У продавца есть m монет достоинством B(1),...,B(l). Может ли купить покупатель вещь стоимости S так, чтобы у продавца нашлась точная сдача (если она необходима).

[Решение]

Задан массив М [1:N] натуральных чисел, упорядоченный по неубыванию, т.е.: M[1]<=M[2]<=...<=M[N].

Написать алгоритм выплаты заданной суммы S минимальным количеством купюp достоинством M(1), ..., M(N).

[Решение]

По матрице A(N,N) построить матрицу B(N,N). Элемент B(I,J) равен максимальному из элементов матрицы А принадлежащем части, ограниченной справа диагоналями, проходящими через A(I,J).

[Решение]

Вводится матрица a(m,n) из 0 и 1. Найти в ней квадратную подматрицу из одних единиц максимального размера.

[Решение]

Вводится матрица a(m,n) из 0 и 1. Найти в ней прямоугольную подматрицу из одних единиц максимального размера (т.е. с максимальным произведением высоты на длину).

[Решение]

Фермер хочет построить на своей земле как можно больший по площади сарай. Но на его участке есть деревья и хозяйственные постройки, которые он не хочет никуда переносить. Для простоты представим ферму сеткой размера MxN. Каждое из деревьев и построек размещается в одном или нескольких узлах сетки. Прямоугольный сарай не должен ни с чем соприкасаться (т.е. в соседних с ним узлах сетки не может ничего быть).

Найти максимально возможную площадь сарая и где он может размещаться.

Дан массив A[N,M]. Необходимо найти максимальную сумму элементов прямоугольного подмассива по всем возможным прямоугольным подмассивам.

[Решение]

Задана матрица натуральных чисел A(n,m). За каждый проход через клетку (i,j) взымается штраф A(i,j). Необходимо минимизировать штраф и

а) Пройти из какой-либо клетки 1-ой строки в n-ую строчку, при этом из текущей клетки можно перейти

1) в любую из 3-х соседних, стоящих в стpоке с номеpом на 1-цу большем;

2) в любую из 8 соседних клеток;

б) Реализовать пункт a) для перехода из клетки (1,1) в (n,m).

[Решение]

Дан выпуклый n-угольник, n=>3, своим обходом по контуру. Разбить его на треугольники (n-3)-мя диагоналями, непересекающимися кроме как по концам, таким образом чтобы

а) Cумма их длин была минимальной;

б) Максимальная из диагоналей имела наименьшую длину.

[Решение]

Задано число А и два вектора b[1..n] и c[1..n].

Найти множество I, являющееся подмножеством множества {1,...,n}, такое, что

является максимальной из всех

возможных

[Решение]

Пусть x=(a₁,a₂,...,a_m) и y=(b₁,b₂,...,b_n) - две заданных строки символов.

Определим d(x,y) как минимальное число вставок, удалений и замен символа, которое необходимо для преобразования x в y.

Например: d(ptslddf,tsgldds)=3

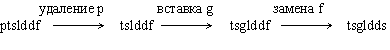
Для заданных x и y найти d(x,y).

[Решение]

Вводится три неотрицательных числа d, i, c и две строки X и Y. Найти преобразование строки X в Y минимальной стоимости. Допустимы следующие три операции:

удалить любой символ из X (стоимость операции d);

вставить любой символ в X (стоимость операции i);

заменить символ в X на произвольный (стоимость операции e).

[Решение]

Даны две строки x и y. Строка x состоит из нулей и единиц, строка y из символов A и B. Можно ли строку x преобразовать в строку y по следующему правилу: цифра 0 преобразуется в непустую последовательность букв A, а цифра 1 - либо в непустую последовательность букв A, либо в непустую последовательность букв B?

[Решение]

Пусть известно, что для перемножения матрицы размера n*m на матрицу размера m*k требуется n*m*k операций. Необходимо определить, какое минимальное число операций потребуется для перемножения n матриц А₁,...А_n, заданных своими размерами n(i)*m(i). При этом можно перемножать любые две рядом стоящие матрицы, в результате чего получается матрица нужного размера.

Замечание:

n(i) - число строк в матрице A_i

m(i) - число столбцов в матрице A_i

n(i)=m(i)+1.

[Решение]

а) Из последовательности, состоящей из N чисел, вычеркнуть минимальное количество элементов так, чтобы оставшиеся образовали строго возрастающую последовательность.

б) Из заданной числовой последовательности A[1..N] вычеркнуть минимальное число элементов так, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего кроме, быть может, одной пары соседних элементов ( одного "разрыва" возрастающей подпоследовательности).

Например: A=(1,2,3,2,4,3,4,6);

Искомая подпоследовательность (1,2,3,2,3,4,6)

Разрыв подчеркнут. ---

б) Из заданной числовой последовательности A[1..N] вычеркнуть минимальное число элементов так, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего кроме, быть может, m пар соседних элементов ( возрастающая подпоследовательность с m "разрывами").

[Решение]

В заданной последовательности целых чисел найти максимально длинную подпоследовательность чисел такую, что каждый последующий элемент подпоследовательности делился нацело на предыдущий.

[Решение]

Возвести число А в натуральную степень n за как можно меньшее количество умножений.

[Решение]

Заданы z и y - две последовательности. Можно ли получить

последовательность z вычеркиванием элементов из y.

[Решение]

Найти максимальную по длине последовательность z, полученную

вычеркиванием элементов как из x, так и из y.

[Решение]

Пусть x и y - две бинарных последовательности (т.е. элементы последовательностей - нули и единицы); x и y можно рассматривать как запись в двоичной форме некоторых двух натуральных чисел.

Найти максимальное число z, двоичную запись которого можно получить вычеркиванием цифр как из x, так и из y. Ответ выдать в виде бинарной последовательности.

[Решение]

Вверх по странице, к оглавлению и навигации.