Олимпиадные задачи по программированию.

(1 вариант). Перевернем (расположим в обратном порядке) отдельно начало и конец массива, а затем перевернем весь массив как единое целое.

(2 вариант, А.Г.Кушниренко). Рассматривая массив записанным по кругу, видим, что требуемое действие - поворот круга. Как известно, поворот есть композиция двух осевых симметрий.

(3 вариант). Рассмотрим более общую задачу - обмен двух участков массива x[p+1]..x[q] и x[q+1]..x[s]. Предположим, что длина левого участка (назовем его A) не больше длины правого (назовем его B). Выделим в B начало той же длины, что и A, назовем его B1, а остаток B2. (Так что B = B1 + B2, если обозначать плюсом приписывание массивов друг к другу.) Нам надо из A + B1 + B2 получить B1 + B2 + A. Меняя местами участки A и B1 - они имеют одинаковую длину, и сделать это легко,- получаем B1 + A + B2, и осталось поменять местами A и B2. Тем самым мы свели дело к перестановке двух отрзков меньшей длины. Итак, получаем такую схему программы:

  p := 0; q := m; r := m + n;
  {инвариант: осталось переставить x[p+1]..x[q], x[q+1]..x[s]}
  while (p <> q) and (q <> s) do begin
  | {оба участка непусты}
  | if (q - p) <= (s - q) then begin
  | | ..переставить x[p+1]..x[q] и x[q+1]..x[q+(q-p)]
  | | pnew := q; qnew := q + (q - p);
  | | p := pnew; q := qnew;
  | end else begin
  | | ..переставить x[q-(r-q)+1]..x[q] и x[q+1]..x[r]
  | | qnew := q - (r - q); rnew := q;
  | | q := qnew; r := rnew;
  | end;
  end;

Оценка времени работы: на очередном шаге оставшийся для обработ- ки участок становится короче на длину A; число действий при этом также пропорционально длине A.

[Назад]

  p1:=1; q1=1; r1:=1;  
  {инвариант: x[p1]..x[p], y[q1]..y[q], z[r1]..z[r]  
   содержат общий элемент }   
  while not ((x[p1]=y[q1]) and (y[q1]=z[r1])) do begin  
  | if x[p1]<y[q1] then begin
  | | p1:=p1+1;
  | end else if y[q1]<z[r1] then begin
  | | q1:=q1+1;
  | end else if z[r1]<x[p1] then begin
  | | r1:=r1+1;
  | end else begin
  | | { так не бывает }
  | end;
  end;
  {x[p1] = y[q1] = z[r1]}
  writeln (x[p1]);
  

[Назад]

Позиция (1,1) проигрышная для игрока, который должен с нее сделать свой очередной ход (фишка уже стоит в позиции (1,1). Все соседние позиции - (1,2), (2,2), (2,1) - выигрышные для делающего текущий ход (они приводят в выигрышную позицию (1,1). Позиции (3,1),(1,3),(3,3) - также проигрышные (любой ход из них приводит в выигрышную позицию, и игрок, делающий следующий ход, выигрывает).

Анализируя позиции дальше, получаем предположение, что позиции с обеими нечетными координатами являются проигрышными для начинающего, все остальные позиции - выигрышные для него. Это действительно так: из проигрышной позиции с обеими нечетными координатами после любого допустимого хода мы попадаем в позицию, где хотя бы одна из координат четная (выигрышную). Из позиции с хотя бы одной четной координатой мы всегда можем опять попасть в позицию с обеими нечетными координатами (проигрышную для делающего очередной ход). Так как последняя позиция (1,1) имеет обе нечетные координаты, то человек, начинающий с позиции, где хотя бы одна из координат четная, всегда сможет сделать так, чтобы после любого его хода фишка была в позиции с обеими нечетными координатами, а в конце концов - в позиции (1,1).

Итак, если i и j нечетные, то первый игрок при наилучших ходах второго всегда проигрывает, иначе - выигрывает.

[Назад]

Будем обозначать текущую ситуацию в игре парой (S,i), где S количество бананов, оставшихся в куче, перед текущим ходом i-ой обезьяны (i равно 1 или 2).

Для того, чтобы (S,1) была выигрышной для игрока 1, среди возможных ситуаций после его хода (S-a₁,2), ... ,(S-a_k,2) должна быть хоть одна проигрышная для игрока 2 (в эту то ситуацию и надо будет перевести игру); если все ситуации выигрышные для игрока 2, то (S,1) - проигрышная для игрока 1 (как бы он не поступал, он все равно проиграет).

Пусть ситуация после хода игрока 1 стала (S',2). Опять же делаем все допустимые ходы из этой позиции и смотрим является ли получившаяся ситуация (S",1) выигрышной, проигрышной или такой, которую мы еще не можем оценить. Если выполняется последняя альтернатива, то из (S",1) мы опять делаем все возможные ходы, анализируем, и т.д.

Если мы в конце концов определили, для кого является выигрышной текущая позиция, то возвращаемся к предыдущему ходу и пытаемся определить, какая позиция для делающего ход и т. д., пока не вернемся к ситуации (L,1).

const l1=200;
s=10;
var a: array [0..l1,1..2] of byte; {в ячейке a[L,i] хранится информация, кто выигрывает в ситуации (L,i)}
b: array [1..2,0..s] of byte; {массив возможных ходов первого и второго игроков в b[i,0] хранится число возможных ходов игрока i}
l,i,j:integer;
Function f(ba:Integer;No: Byte): Byte;
Var i,p,r: Byte; {рекурсивная функция вычисления (L,i)}
Begin {f=i, если в (ba,i) выигрывает i}
if Ba<0 {после хода монет <0?}
Then f:= 3-No {выигрыш игрока с номером 3-Nо}
else if ba=0 {монет = 0?}
then begin {выигрыш No}
f:=No;
a[ba,no]:=no;
end
Else if a[ba,no]<>0 {в этой ситуации мы уже были}
Then F := a[ba,no] {в ней выигрывает a[ba,no]}
Else
Begin {эту ситуацию мы еще не рассматривали}
r := 0;
{мы будем делать все возможные ходы}
For i := 1 to b[No,0] do
if ba-b[no,i]>=0 {если ход возможен, то делаем его}
then r := r or F(Ba-B[No,i],3-No);
if r=0 then r:=no;
If (No and R)<>0 {есть выигрышный ход?}
Then p := No {да, (ba,i)=No}
Else p := 3-No; {нет, (ba,i)=3-No}
A[Ba,No]:=p; {запоминаем эту информацию}
f:=p;
End;
end;
begin
for i:=0 to l1 do
for j:=1 to 2 do A[i,j] := 0;
write('s=');
readln(b[1,0]); {b[1,0] = количество ходов первого игрока}
for i:=1 to b[1,0] do
begin
write('a',i,'='); {сами ходы}
Readln(b[1,i]);
end;
write('k=');
Readln(b[2,0]); {b[2,0] = количество ходов второго игрока}
For j := 1 to b[2,0] do
begin
write('b',j,'=');
Readln(b[2,j]); {ввод ходов}
end;
repeat {для данных ходов вводятся значения L}
write('L='); {число бананов}
readln(l);
if f(l,1)=1 {вызов рекурсивной функции-проверки}
then writeln('1-я выиграла')
else writeln('1-я проиграла');
for i:=1 to b[1,0] do {распечатка результатов возможных ходов}
if (l-b[1,i])>=0 {из начальной позиции L}
then writeln('b=',b[1,i],' winner=',a[l-b[1,i],2]);
writeln;
until false;
end.

[Назад]

Идея решения аналогична изложенной в задаче про обезьян.

[Назад]

Если n=1, и единственное слово начинается и заканчивается на одну и ту же букву, то цепочка построена.

Для того, чтобы можно было переупорядочить слова A₁, ..., A_n из набора A в "цепочку", необходимо, чтобы совокупность букв, на которые заканчиваются слова, совпадала с совокупностью букв, на которые эти слова начинаются (другими словами, чтобы каждой завершающей букве слова соответствовала такая же начальная буква какого-то слова). То, что это не достаточное условие, показывает пример: AB, BC, CA, DE, ED. "Цепочку" построить нельзя.

Так как цепочка обязана пройти через каждое слово, то все равно, с какого слова набора A начинать. Возьмем слово A₁. Удаляем его из множества A: A:=A\A₁. Ищем в A какое-нибудь слово A_i, начинающееся с последней буквы слова A₁ (такое слово всегда существует, так как мы считаем, что необходимое условие, упомянутое выше, выполняется). Удаляем A_i из A: A:=A\A_i, ищем в A какое-нибудь A_j, начинающееся с последней буквы A_i и т.д. Продолжаем до тех пор, пока либо все слова A₁, ... ,A_n не войдут в цепочку (тогда задача решена), либо пока не окажется, что A не пусто, и в нем нет слова, начинающегося на последнюю букву x последнего слова (кстати, из необходимого условия следует, что эта буква x совпадает с первой буквой первого слова). Мы нашли какую-то подцепочку.

Пример: A=(AB,BC,CA,BD,DC,CB).

Подцепочка1: AB,BC,CA.

Цепочка существует: AB,BD,DC,CB,BC,CA.

Пусть мы нашли подцепочку 1. Берем опять какое-нибудь слово из A в качестве начального для очередной подцепочки и опять повторяем построение следующей подцепочки, и т.д.

В конце концов пусть множество A стало пустым, и весь начальный набор слов A₁, ... ,A_n распался на k подцепочек. Начнем их склеивать:

Пусть в подцепочках i и j соответственно есть слова u и v такие, что в u и v совпадают первые буквы. Пусть цепочка i имеет вид i=BuC, а j=EvD (тут B,C,D,E - некоторые последовательности слов). Склеенная из i и j цепочка будет иметь вид

EuCBvD.

(Проверьте, что такая склейка корректна!)

Склеивая все подцепочки, получим искомую цепочку. Если на каком-то шаге окажется, что склейка никаких двух подцепочек невозможна, то задача неразрешима.

Пример 1. Для приведенного в предыдущем примере набора слов будет 2 подцепочки:

AB, BC, CA и

BD, DC, CB.

У них совпадают первые буквы в словах BC и BD. После склейки получаем

AB, BD, DC, CB, BC, CA.

Пример 2. A=(ACA, BB). Две подцепочки: ACA и BB. Слов с совпадающими первыми буквами в них нет, задача неразрешима.

Вариант #2 решения задачи.

Если при составлении цепочки оказалось, что в наборе A нет слова с первой буквой, совпадающей с последней буквой последнего слова A_j цепочки, то A_j "отщепляем" от нее и пытаемся найти другое подходящее слово. Если это не удается, то "отщепляем" очередное последнее слово цепочки и т.д. Если на каком-то шаге A пусто, то задача решена, иначе если на каком-то шаге цепочка стала пустой, то задача неразрешима.

Пусть есть набор слов A=(A₁, ... ,A_n). Каждому слову приписан его уникальный номер, равный индексу. Слова упорядочены по возрастанию индекса.

Цепочка = A₁
A=A\A₁; инд=1.
Пока (A не пусто) и (цепочка не пустая) повторять
нц
Если в A есть подходящее слово с индексом > инд
то приписываем к цепочке это слово,
слово удаляем из A
инд=1
иначе "отщепляем" от цепочки последнее слово A_j
инд=j
A_j заносим в A
кц
Если A пусто, то цепочка найдена
иначе задача не имеет решения.

Этот метод называется "перебор с возвратом" ("backtracking").

[Назад]

Предположим, что левая фишка (будем называть ее Ф₁) можем ходить только вправо, а правая фишка Ф₂ - только влево, и ход передавать нельзя. Решение задачи в первоначальной постановке сводится к решению задачи при налагаемых выше ограничениях.

Пусть первый ход делает Ф₁. Ф₁ выигрывает, если количество клеток между фишками d(Ф₁,Ф₂) (вначале оно равно m-2) не делится нацело на k+1. Действительно, пусть Ф₁ делает такой ход, что d(Ф₁,Ф₂) кратно k+1. Какой бы ход не сделала Ф₂ (например, на L клеток влево), Ф₁ следующим ходом смещается на k+1-L клеток вправо, и, таким образом, после хода Ф₁ расстояние d(Ф₁,Ф₂) снова кратно k+1. А так как 0 также делится на k+1 нацело, то наступит момент, когда d(Ф₁,Ф₂)=0 и предыдущий ход был ходом Ф₁, т.е. Ф₂ проиграла. Если (m-2) mod (k+1)=0, то Ф₁ при наилучших ходах Ф₂ проигрывает.

Если разрешить фишкам ходить как влево, так и вправо, то всегда выигрывает та фишка, после хода которой d(Ф₁,Ф₂) кратно k+1.

[Назад]

Последовательность строится так: сначала пишется 0, затем повторяется следующее действие: уже написанную часть приписывают справа с заменой 0 на 1, 1 на 0, т.е.

0 -> 01 -> 0110 -> 01101001 ->...

Докажите, что предложенная последовательность удовлетворяет условию задачи.

Если не смогли этого сделать, то вот доказательство:

Будем нумеровать цифры последовательности, начиная с нуля. Итак, a(0)a(1)=01, a(2)a(3)=10=a(1)a(0). Отметим, что последовательность состоит из 'кирпичиков' 01 и 10 (любые a(2k)a(2k+1) есть либо a(0)a(1), либо a(1)a(0)). Любой отрезок четной длины, начинающийся с элемента с четным индексом a(2k) имеет поровну нулей и единиц. Предположим, что в M есть три смежных одинаковых отрезка. Если есть такие отрезки, то есть и отрезки минимальной длины. Можно считать, что сначала идет начальный отрезок P, затем подряд три смежных одинаковых отрезка S₁,S₂ и S₃ минимальной длины, S₁=S₂=S₃= =S:

P S₁ S₂ S₃.

Будем обозначать длину отрезка A через IAI.

Есть 4 возможных варианта:

1) IPI=2k, ISI=2l.

Будем писать 0* вместо 01 и 1* вместо 10. С помощью этих символов последовательность M записывается так же, как и раньше:

Значит и P, и S можно записать с помощью символов 0* и 1*; начальный отрезок P будет состоять из k знаков 0* и 1*, а S - из l знаков. Уберем звездочки у цифр - последовательность M от этого не изменится. А из P,S₁,S₂ и S₃ мы получим новые отрезки P', S₁',S₂' и S₃' с длинами вдвое меньшими. Отрезки S₁',S₂' и S₃' остаются одинаковыми, а длина каждого из них станет l. Мы получили противоречие с утверждением о минимальности длины S.

2) IPI=2k, ISI=2l+1.

Отрезок S₁ начинается элементом с четным индексом. Длина отрезка S₁ S₂ четная (она равна 4l+2), и в нем одинаковое число нулей и единиц. Длина S₁ нечетная, и, без нарушения общности, предположим, что нулей в S₁ больше, чем единиц, тогда в S₂ единиц будет больше чем нулей?! Противоречие с тем, что S₁=S₂.

3) IPI=2k+1, ISI=2l+1.

Отрезок S₂ S₃ имеет четную длину и начинается элементом с четным индексом. Далее рассуждения аналогичны приведенным в пункте 2.

4) IPI=2k+1, ISI=2l.

Последний элемент отрезка P имеет индекс a(2k) (вспомните, что нумерация элементов начинается с нуля). Пара a(2k) a(2k+1) есть либо 01, либо 10, и всегда a(2k)<>a(2k+1). Первые элементы S₁,S₂ и S₃ будут, соответственно, a(2k+1), a(2k+2l+1), a(2k+4l+1). Поэтому из совпадения S₁=S₂=S₃ следует, что

Следовательно, так как

то мы можем считать, что повторяющиеся отрезки S₁ S₂ S₃ начинаются в позиции a(2k), IPI=2k, ISI=2l, а этот случай уже разобран в пункте 1.

[Назад]

Рассмотрим сначала случай, когда a, b, c, x_i - натуральные.

1) Разбивка на слагаемые.

Если a<c, то задача неразрешима, если a лежит на [c,d], то задача решена.

Пусть a>d. Минимальное число слагаемых будет тогда, когда каждое из слагаемых будет как можно больше. Введем функцию ceil(x)=k+1, если k<x<=k+1, k - целое. Покажем, что в случае, если разложение существует, то необходимо ceil(a/d) слагаемых.

Пусть k=ceil(a/d). Если мы возьмем k слагаемых по d, то превышение над a будет p=k*d-a. Каждое из k слагаемых мы можем уменьшить не более чем на d-c. Количество уменьшаемых слагаемых должно быть n=ceil(p/(d-c)). Если n>k, то разложения не существует (слагаемых, которые надо уменьшить, больше, чем у нас есть, другими словами, a div c = a div d, и a mod c <> 0, a mod d <> 0). Если n<=k, то L, L=p div (d-c), слагаемых уменьшаем на (d-c), одно слагаемое - на p mod (d-c), остальные остаются без изменений (равными максимальному).

Если a, b, c, x_i - целые, то алгоритм практически не изменяется.

2) Разбивка на сомножители.

Метод решения этой задачи аналогичен использованному при решении задачи о нахождении максимальной по длине возрастающей подпоследовательности введенной последовательности (см. задачу 20 главы "Рекуррентные соотношения и динамическое программирование").

Опять будем рассматривать только случай a>d.

Обозначим через L упорядоченное по возрастанию множество делителей числа A, лежащих на отрезке [c,d], количество делителей не превышает 2*SQRT(A) (если a=f*g, то f<=SQRT(a), g>=SQRT(a), всего разных f - не более SQRT(a), столько же и разных g). Пусть L₁ минимальный элемент из L, a L₂- максимальный. В массив S[1..k] занесем по возрастанию все делители числа a (включая и само число a=S[k]), начиная с минимального элемента из L. Из утверждения выше следует, что k<=2*SQRT(A)+1.

Будем искать минимальную по длине последовательность элементов массива S, ведущую из множества L в число a=S[k] такую, что каждый последующий элемент последовательности при делении на предыдущий дает частное, принадлежащее множеству L, и нулевой остаток.

Заведем массивы B[1..k] и C[1..k]. В B[i] будем заносить индекс последующего элемента в подпоследовательности минимальной длины, ведущей из S[i] в S[k] (B[i]=0, если в a из S[i] попасть невозможно), в C[i] будет храниться число элементов в этой минимальной последовательности (отметим, что мы рассматриваем только такие последовательности, у которых частное от деления последующего члена последовательности на предыдущий принадлежит множеству L, а остаток от деления нулевой).

Сначала во все элементы C, кроме последнего, занесем какое-нибудь большое число, например 2*A. Если C[i]=2*A, то будем считать, что последовательности элементов, идущей от S[i] к S[k], пока не обнаружено.

После заполнения матриц A и B мы находим минимальную длину цепочки, ведущей из множества L в число a.

for i:=1 to k-1 do C[k]:=2*A; {последовательности нет}
C[k]:=1; {последовательность из одного элемента A}
B[k]:=0; {предыдущего элемента нет}
for i:=k-1 downto 1 do
for j:=i+1 downto k do
if (S[j] div S[i] >=L₁) and {частное S[j]/S[i]}
(S[j] div S[i] <=L₂) and {принадлежит L, и}
(S[j] mod S[i] =0) {остаток нулевой}
then if C[i]>C[j]+1 {если длина обнаруженной}
then begin {сейчас подпоследовательности,}
{идущей от S[i] к S[k], меньше, чем}
C[i]:=C[j]+1; {ранее найденная, то кор ректируем длину и индекс следующего элемента}
B[i]:=j
end;
i:=1; min:=2*A; j:=0;
while S[i]<=L₂ do
begin
if C[i]< min
then begin
min:=C[i]; {корректируем минимум}
j:=i; {сохраняем индекс первого элемента}
end;
i:=i+1
end;
if j=0
then writeln('Разложения не существует')
else begin
writeln('Разложение:');
write(A[j]);
for i:=1 to min-1 do
begin
P:=j;
j:=B[j];
write(A[j]/A[p]) {распечатка сомножителя}
end
end

В случае, если a, c, d, x_i - целые, в массив S помещаем в порядке возрастания модуля все делители числа A, начиная с минимального элемента в L. Далее - аналогично.

[Назад]

См. решение задачи о том, является ли введенное слово периодическим повторением какого-то другого слова (Задача 21).

[Назад]

Решается аналогично задаче 23 (глава "Рекуррентные соотношения и динамическое программирование").

[Назад]

Если последовательности B и C совпадают, то вычеркнутых букв определить нельзя.

Если B и C различаются ровно в одной позиции (т.е. в A были вычеркнуты соседние буквы), то определить вычеркнутые буквы можно, а последовательность A - нет (пример: A='ABCDB', B='ACDB', C='ABDB').

Чуть-чуть упростим задачу. Уберем из начала и конца последовательностей B и C все совпадающие элементы. Получим последовательности B' и C'. Пример B='albce', C='alcde', B'='bc', C'='cd', т.к. первые два и последний символ у B и C совпадают. Если мы сможем восстановить слово, из которого получается B' и C', то мы сможем восстановить и A.

Пусть B'=b₁b₂b₃ ... b_k

C'=c₁c₂c₃ ... c_k.

Если b₁=c₂=b₃=c₄= ... и (*)

C₁=b₂=c₃=b₄= ...,

то определить последовательность A нельзя, выброшенные буквы

- это b₁ и c₁.

Пример: B='abab', C='baba'. В качестве A можно взять как

'babab', так и 'ababa').

Если же (*) не выполняется, то можно найти и A, и вычеркнутые

буквы. Мы находим такие элементы в B' и C', что c(i)=b(i+1) и b(i)<>c(i+1) (или c(i)<>b(i+1), а b(i)=c(i+1)), и получаем начальную строчку A=b(1) ... b(i)b(i+1)c(i+1)b(i+2)

... b(k) (или A=c(1) ... c(i)c(i+1)b(i+1)c(i+2) ... c(k)).

Пример: B'='bc'

C'='cd'

Слово из которого получается и B' и C' - 'bcd'.

[Назад]

Эту же последовательность можно записать и так:

2, 4, 8, 16, 32, 64, 128, ...

Очередной член последовательности - 28.

[Назад]

Члены последовательности есть запись числа 6 в двоичной, троичной, четверичной, пятеричной шестеричной, ... системах счисления. Все остальные члены последовательности равны 6.

[Назад]

Определим вначале ситуации, когда можно можно определить фальшивую монету за одно взвешивание. Это возможно сделать, если:

есть две неизвестные монеты и одна стандартная (заведомо не

фальшивая);

есть три неизвестные монеты и известен вес фальшивой монеты

(т.е. информация о том, больше или меньше ее вес).

Алгоритм:

Разобьем 13 монет на 3 части: 4,4 и 5 монет.

1. вес монет в первых частях равны. Тогда это стандартные монеты. Будем обозначать их через с а возможные фальшивые монеты через ф.

2-е взвешивание

ссс и ффф (остались неопределенными только фф из третьей части).

Если веса равны, то фальшивая среди оставшихся двух. Если

нет, то среди взвешенных трех, но ее вес известен.

2. Веса монет в первых частях не равны. Тогда монеты из третьей части - стандартные монеты. Определим взвешенные монеты как т (тяжелые) или л (легкие) в зависимости от результатов взвешивания.

2-е взвешивание

ссст и тттл

Если веса равны, то фальшивая среди оставшихся трех легких. Если нет, то возможны следующие ситуации.

2.1. ссст легче тттл. Понятно, что фальшивая монета находится среди трех тяжелых монет.

2.2. ссст тяжелее тттл. Понятно, что фальшивая монета находится среди двух монет: тяжелой монеты слева или легкой справа.

Поэтому фальшивую монету можно определить за одно оставшееся

взвешивание.

[Назад]

{Задача "Быки и коровы"

Пользователь загадывает число из 4 цифр, каждая из которых от 1 до 6, причем все цифры различны. Разработать алгоритм, который угадывает число по следующим правилам: выводится число и пользователь сообщает, сколько в нем "быков" и "коров", т.е. сколько цифр стоят на своих местах и сколько цифр содержатся в обоих числах, но совпадают лишь по значению. Например, пусть загадано число 1264, спрошено 1256. В этом случае 2 быка (1,2) и одна корова (6)

б) Правила игры те же, но загадывается 6-значное число с цифрами от 1 до 9, причем среди цифр допускаются одинаковые.

Примечание : Спрошенное число должно удовлетворять правилам для загадываемого; компьютеру на ход дается 1 минута .

Итак, 1-ое что приходит в голову играть по следующему правилу: называть первое попавшееся число, которое может быть задуманно, т.е. при сопоставлении любого ранее спрошенного числа с новым должно получится такое-же количество 'быков' и 'коров'. Число будем представлять в виде массива цифр.}

const MaxSgn = 6; {Максимальное значение в числе}
Sgn = 4; {Количество цифр в числе}
type S = 1..MaxSgn;
Numb = array[1..Sgn] of S;
function cows(n1,n2:Numb):byte;
{Сравнивает два числа и возвращает результат сравнения в виде <количество быков>*10+<количество коров>}
var i1,i2 : 1..Sgn;
a : byte;
begin
{Необходимо сравнивать все цифры первого числа со всеми цифрами второго}
a:=0;
for i1:=1 to Sgn do
for i2:=1 to Sgn do
if n1[i1]=n2[i2] then
if i1=i2 then a:=a+10 {Встретился 'Бык'}
else inc(a);
cows:=a;
end;
type Step = Record {Информация об одном вопросе - ответе}
n : Numb; {Спрошенное число}
answer : byte; {Ответ}
end;
Game = array[1..32] of step;
{Информация о всех вопросах - ответах}
var Nstep : byte; {Номер текущего шага}
Info : Game;
Curnumb : Numb; i,j : integer; b : boolean;
BEGIN
clrscr;
for i:=1 to Sgn do Curnumb[i]:=i;
Nstep:=0;
while true do
{Пока не будут перебраны все числа или не найденно решение}
begin
{Спросить текущее число}
for i:=1 to Sgn do write(Curnumb[i]);
write(' ? ');
inc(Nstep);
Info[Nstep].n:=Curnumb;
readln(Info[Nstep].Answer);
{Пользователь должен ввести число, первая цифра которого 'Быки', вторая - 'Коровы'}
if (Info[Nstep].Answer div 10+Info[Nstep].Answer mod 10)>Sgn then
begin writeln('Плохая игра !'); exit; end;
{'Быков' и 'Коров' вместе не может быть больше, чем цифр}
if Info[Nstep].Answer=10*Sgn then exit;
{Далее идет генерация нового числа}
repeat
i:=Sgn;
{Увеличение числа на 1-цу}
while (i>=1) and (Curnumb[i]=MaxSgn) do
begin
Curnumb[i]:=1;
dec(i);
end;
if i<1 then
begin {Все числа перебраны, а ответ не найден}
writeln('Вы неправильно отвечали !'); exit; end;
inc(Curnumb[i]);
b:=true;
{Проверка на встречающиеся одинаковые цифры}
for i:=1 to Sgn do
for j:=i+1 to Sgn do
b:=b and (Curnumb[i]<>Curnumb[j]);
for i:=1 to Nstep do b:=b and (cows(Curnumb,Info[i].n)=Info[i].Answer);
until b;
end; {while}
END. {program}

Итак, наша программа работает следующим образом: мы путем последовательного увеличения на 1 генерируем все возможные 6-значные числа, отбираем среди них те, в которых все цифры различные, и, наконец, те из них, которые удовлетворяют хранящимся в массиве Info ответам, задается пользователю в качестве вопроса. Возникает ряд резонных вопросов: сколько всего интересующих нас 4-значных цифр и какая их часть не содержит повторений.

За сколько шагов может угадать ответ самый быстрый алгоритм и насколько хороша наша стратегия?

Давайте попытаемся ответить на них. Итак сколько всего чисел? Пусть k цифр и m позиций. В первой позиции может стоять любая

Из k цифр, что нам дает k вариантов. Во второй-также любая из k цифр, т.е. k². И так далее m раз, т.е. всего k^m вариантов. Обобщим эту идею.

Определение: размещение с n повторением из k элементов по m называется m-элементный массив натуральных чисел, каждое из которых не превосходит k.

Утверждение: Число размещений с повторениями из k по m равно k^m. Доказательство проводим по индукции:

Базис индукции: При m=1 у нас ровно k вариантов.

Индуктивный переход: Пусть утверждение верно при m=n-1. Докажем, что оно верно при m=n. Зафиксируем число 1. Справа к этому числу припишем kⁿ⁼¹ размещений из k по n-1. Аналогично поступим с 1,2,3...k. Получим k^n-1*k=kⁿ вариантов.

Таким образом, число 4-значных чисел с цифрами от 1 до 6 равно 6⁴=1296. Теперь посмотрим, сколько из них не содержит повторяющихся цифр.

Определения: размещением из k элементов по m называется m-элементный массив каждая компонента которого не превосходит k и среди них не встречаются одинаковые. Очевидно, что множество размещений не пусто лишь при m<=k.

Число размещений из k по m принято обозначать A.

Утверждение A=k*(k-1)*...(k-m+1)=k!/(k-m+1)!

Доказательство проводим по индукции:

Базис индукции: При m=1 у нас ровно k вариантов.

Индуктивный переход: Пусть утверждение верно при m=n-1. Выберем любое из k!/(k-n+1)! размещений из k по n-1. Чисел, которые в нем не участвуют-(k-n+1). Приписывая их поочередно справа к выбранному размещению мы получим (k-n+1) вариантов. Перебирая все размещения:

Таким образом,число 4-значных чисел с цифрами от 1 до 6 без повторений равно A46=6*5*4*3=360, т.е. в 3 раза меньше, чем число вариантов, которые мы перебирали. Итак мы нашли один способ для оптимизации нашей программы: генерировать не все числа, а лишь те, которые не содержат повторяющихся цифр. Возьмем это на заметку, а сейчас попробуем оценить максимальное число шагов, за которое отгадывает лучший игрок. Вариантов ответа у нас:

Пусть угадано 4 цифры. Среди них могут быть 2,1,0 "быков". Пусть угаданы 3 цифры. Среди них могут быть 3,2,1,0 "быков". И так далее: получаем 3+4+2+1=10 вариантов.

Таким образом за каждый вопрос количество допустимых чисел уменьшается, если мы рассматриваем худший случай, не более чем в 10 раз. Число шагов, за которое угадывает лучший игрок, не менее чем [log₁₀ 360]+1=3

Ну а теперь попытаемся повысить эффективность работы программы. Как уже было отмечено выше, нам достаточно перебрать не 1096 комбинаций, а всего лишь 360. Это не отразится на быстроте угадывания, т.е. числе шагов, так как не изменим стратегии "первый попавшийся из подходящих", но уменьшит время обдумывания хода.

Генерировать числа будем следующим образом: для начала выберем множество цифр, которое в него входит, ну а затем будем переставлять элементы этого множества между собой. Множество цифр удобно, для наших целей, представить в виде массива длины 4, элементы которого расположены в порядке возрастания. Будем генерировать эти массивы в лексикографическом порядке, т.е. сначала сравниваются первые цифры, если они равны - вторые, и так далее. То есть:

Значит, мы должны увеличить самую правую цифру, какую это возможно, и уменьшить затем те цифры, какие стоят за ней. Заметив, что номер цифры, которую нужно увеличивать, уменьшается на 1, а как только последний элемент массива можно будет увеличить, скачкообразно становится равной длине массива, приходим к следующему алгоритму:

{A-массив который содержит текущие комбинации}

Var
p:integer;
{номер элемента ,который увеличивается в данный момент}
Var
i:integer;
for i:=1 to n do
a[i]:=i;{Начальное значение}
p:=n;{увеличивается крайняя правая цифра}
while p>=1 do
begin
{Write(A)}-{Последовательность готова};
for i:=k downto p do
A[i]:=A[p]+i-p+1;
if a[k]=n then dec(p);
else p:=k;
end;

Для генерирования всевозможных перестановок множества служит следующая идея: Пусть у нас сформированы всевозможные перестановки длины N-1. Вставляя оставшийся элемент в каждую перестановку во все возможные позиции, мы получим все комбинации длины n. Например, число 1 в перестановку 2 3 можно вставить следующими 3-мя способами:

Следует отметить, что получающиеся перестановки обладают приятным свойством: каждая перестановка получается из предыдущей путем обмена двух соседних элементов. Применяя эту идею рекурсивно, мы получим, например, следующую последовательность перестановок:

Для применения этого алгоритма в рекурсивной форме нам понадобится хранить всевозможные перестановки. Давайте попытаемся привести этот алгоритм к нерекурсивной форме. Для i-го элемента нам необходимо знать:

Куда он сейчас движется - вправо или влево.

Мы приходим к следующему алгоритму:

{B - массив элементов перестановки}
{Direc - массив направлений, i-й элемент равен TRUE, если тело i движется вправо}
{Posit - массив положения i-го элемента в перестановке n-i элементов}
for i:=1 to n do
begin
B[i]:=i;
Posit[i]:=1;
Direc[i]:=TRUE;
end;
Posit[n]:=0;

Давайте попытаемся привести этот алгоритм к нерекурсивной форме. Для i-го элемента нам необходимо знать:

Куда он сейчас движется-вправо или влево.

Номер возможного из n-i+1 мест в перестановке длине n-i, которое он сейчас занимает.

Мы проходим к следующему алгоритму:

{В-массив элементов перестановки}
{Direc-массив направлений. i-й элемент равен true, если число i движений вправо}
{Posit- массив положения i-го элемента в перестановке
n-i элементов}
For i:=1 to n do
begin
b[i]:=i;
posit[i]:=1;
direc[i]:=true;
end;
posit[n]:=0;
i:=1;
while i<n do
begin
direct[i]:=not direct[i];
posit[i]:=1;
if direct[i] then inc(x);
inc(i)
end;
if i<n then
begin
if pirof[i] then k:=c[i]+x
else k:=n-i+1-c[i]+x;
b[k]<->b[k+1];
inc(posit[i])
end
end;
И, наконец, новый вариант программы игры
Const MaxSgn=6;
Sgn=4;
Type s=1..MaxSgn; {цифра}
Numb=array[1..Sgn] of s;
function cows(n1,n2:Numb):byte;
{Сравнивает два числа и возвращает результат сравнения в виде <количество быков>*10+<количество коров>}
var i1,i2 : 1..Sgn;
a : byte;
begin
{Необходимо сравнивать все цифры первого числа со всеми цифрами второго}
a:=0;
for i1:=1 to Sgn do
for i2:=1 to Sgn do
if n1[i1]=n2[i2] then
if i1=i2 then a:=a+10 {Встретился 'Бык'}
else inc(a);
cows:=a;
end;
type Step = Record {Информация об одном вопросе - ответе}
n : Numb; {Спрошенное число}
answer : byte; {Ответ}
end;
Game = array[1..32] of step;
{Информация о всех вопросах - ответах}
var NStep:byte;
Info:game;
Procedure testnumber;
{процедура проверяет, удовлетворяет ли входное число ранним ответам, и, если да, то задает его в качестве вопроса. В случае, если число угадано, заканчивает игру}
Var i:byte;
begin
for i:=1 to nstep do
if cows(n,info[i].n)<>info[i].answer then Exit;
inc(Nstep);
info[nstep].n:=n;
for i:=1 to sgn do write(n[i]);
write(' ? ');
readln(info[nstep].answer);
if info[nstep].answer=sgn*10 then
halt;
{игра окончена}
end; {test number}
Var tset{текущее n-элементное подмножество}
,tn:number;
i,j,k,l:byte;
direc:array[1..sgn] of boolean; posin:array[1..sgn] of byte;
begin
{инициализация}
nstep:=0;
for i:=1 to sgn do tset[i]:=i; i:=sgn;
while i>=1 do
begin
tn:=tset;
for j:=1 to sgn do begin
posit[i]:=1;
direct[i]:=true;
end;
posit[sgn]:=0;
j:=1;
testnumber(tn);
while j<sgn do
begin
j:=1;
k:=0;
while posit[j]=sgn-j+1 do
begin
posit[j]:=1;
direct[j]:=not direct[j];
if direct[j] then inc(x);
inc(j);
end;
if j<sgn then
begin
if direct[j] then l:=posit[j]+n;
else l:=sgn-j+1+posit[j]+k;
inc[posit[j];
end;
end;
writeln('Плохая игра');
end.

[Назад]

Тесты должны проверять не только работу программы на корректных данных, но и на некорректных. Например:

Какие еще тесты можно предложить?

[Назад]

Решение задачи 19 (Прохоров В.В.).

Обозначим условия через F(x,y):

т.е. F(6,-2) должна равняться и True и False одновременно! Следовательно такого < условия выполнения итерации > не существует. Задача алгоритмически не разрешима. Но если мы разрешим использовать в условии обращение к функции F(x,y), которая возвращает всегда логическое значение False, и изменяет аргументы x и y требуемым образом, то тело цикла не будет выполняться, и в этом случае задачу можно решить.

[Назад]

Во всех узлах (трубках) схемы мы должны получить состояние G_i'. Первоначально установим G₁, G₂ и G₃ в G₁', G₂' и G₃', выбрасывая, по необходимости, шарики через входы A, B и С соответственно. Для того, чтобы G₁,G₂ и G₃ оставались в состоянии G₁', G₂' и G₃' необходимо, чтобы через каждый из входов забрасывалось лишь четное число шариков.

Если проследить за шариками, заброшенными в игровой автомат, то мы можем заметить, что результат хода, например, ABC аналогичен результату хода BCA, т.е. от порядка заброски шариков ничего не зависит!

Рассмотрим узлы,состояние которых может меняться при забрасывании шариков через вход A, т.к. при выбранной методике забрасывания только четного числа

шариков через входы всегда G₁=G₁', то состояний G₆ G₄ G₇ может быть лишь 2³=8, от 000 до 111. Если мы будем забрасывать через A пары шариков, то при забросе серии максимум из 8 пар шариков какое-то состояние G₆ G₄ G₇ должно обязательно повториться на протяжении серии, а далее состояния будут циклически повторяться, и случай с забрасыванием более 8 пар шариков сводится к случаю с количеством пар, не превосходящим 8.

Аналогично, для забрасывания шариков через B мы получаем серию из не более чем 2⁵=32 пар шариков, на протяжении которой будут установлены все возможные состояния G₄ G₅ G₆ G₇ G₈, а для входа C серия, как и для A, будет иметь длину не более 8 пар.

Перебирая все возможные комбинации A2x B2y C2z забрасывания шариков (тут A2x обозначает серию из 2X забрасываний шариков через вход A, 0<= x,y <=8, 0<=z<=32 ) получаем либо комбинацию-решение задачи, либо определяем отсутствие решения.

[Назад]

Для решения данной задачи введем так называемую функцию отказов F(j), принимающей целочисленные значения [ Ахо А. и др. Построение и анализ вычислительных алгоритмов., М., 1979, с.386]. Функция F задается так: F(j) -- наибольшее число s<j, для которого A₁ A₂ ... A_s -- суффикс цепочки A₁, A₂, ..., A_j, т.е.

A₁ A₂ ... A_s = A_j-s+1 A_j-s+2 ... A_j

Если такого s=>1 нет, то F(j)=0.

Определим функцию F^(m)(j) следующим образом:

1) F⁽¹⁾ (j)=F(j)

2) F^(m) (j)=F(F^(m-1) (j)) для m>1.

Будем вычислять функцию F итеративно. По определению F(1)=0.

Допустим, что вычислены F(1), F(2), ... , F(j). Пусть F(j)=i. Чтобы вычислить F(j+1) исследуем A_j+1 и A_i+1 . Если A_j+1 = A_i+1 , то

F(j+1)=F(i)+1 ,

поскольку

A₁ A₂ ... A_i A_i+1 = A_j-i+1 A_j-i+2 ... A_j A_j+1 .

Если A_j+1 <> A_i+1 , то тогда надо найти наибольшее значение i, для

которого

A₁ ... A_i = A_j-i+1 ... A_j и A_i+1 = A_j+1 ,

если такое i существует. Если такого i нет, то очевидно, что F(j)=0. Пусть i₁ , i₂ , ... - наибольшее, второе по величине и т.д. значения i, для которых

A₁ A₂ ... A_i = A_j-i+1 ... A_j .

С помощью простой индукции убедимся, что

i₁ =F(j), i₂ =F(i₁)=F⁽²⁾(j), ..., i_k =F(i_k-1)=F^(k)(j), ....

Итак, в случае A_j+1 <> A_i+1 находим наименьшее m, для которого либо

1) F^(m)(j)=u и A_j+1 = A_u+1 , и полагаем тогда F(j+1)=u+1,

либо

2) F^(m)(j)=0 и A_j+1<> A₁, и тогда F(j+1) полагаем равным 0.

Алгоритм вычисления F следующий:

begin
F[1]:=0;
for j:=2 to n do
begin
i:=F[j-1];
while ( A[j]<>A[j+1] ) and ( i>0 ) do
i:=F[i];
if ( A[j]<>A[i+1] ) and ( i=0 )
then F[j]:=0
else F[j]:=i+1;
end;
end.

Этот алгоритм вычисляет F за O(n) шагов. Чтобы доказать это,

покажем, что сложность оператора while при работе программы (пропорциональная числу уменьшений значения i оператором i:=F[i]) линейно зависит от N.

Единственный способ увеличить i в этом фрагменте программы -это выполнить оператор F[j]:=i+1 в третьей от конца программы строке. Этот оператор может выполняться не более N-1 раза, следовательно, и уменьшение i в операторе while может произойти не более N раз. Остальная часть алгоритма имеет сложность O(n), и поэтому и весь алгоритм имеет сложность O(n).

Итак, мы вычислили F(n)=U, это означает, что

A₁ A₂ ... A_U = A ... A_N-U+1 (*)

Для того, чтобы последовательность

A₁ ... A_N

была периодической необходимо и достаточно, чтобы длина общей части двух строк в (*)

A_N-U+1 ... A_U

была кратна длине периода (в качестве периода последовательности тут выступает строка A₁ ... A_N-U ).

Действительно, если A₁ ... A_N-U = A_N-U+1 ... A_2(N-U) , то по

свойству (*) и A_N-U+1 ... A_2(N-U) = A_2(N-U)+1 ... A_3(N-U) и т.д.

Для окончательного решения задачи

1) найдем длину l перекрывающейся части строк в (*)

l=U-(N-U+1)+1 =2*U-n;

в случае l<=0 последовательность A₁ ... A_N непериодическая. Стоп.

2) Если l>0 , то проверим, делится ли нацело l на длину периода (т.е. на N-U)

l mod (N-U) = (2U-N) mod (N-U) = - ((N-U)-U) mod (N-U) =

= U mod (N-U) = R

Если R=0, то последовательность периодическая с периодом A₁ ... A_N-U ,

иначе - нет.

[Назад]

Назовем скобочное выражение элементарным, если оно представимо в виде (S), где S - правильное скобочное выражение. Очевидно, что каждое непустое скобочное выражение можно единственным образом представить в виде

ES,

где

E - элементарное скобочное выражение;

S - скобочное выражение (возможно, пустое).

Обозначим через S(n) число правильных скобочных выражений с 2n скобками. Тогда число элементарных скобочных выражений с 2n

скобками есть S(n-1). Таким образом

S(n)=(S(i-1)*S(n-i)).

Замечая, что S(0)=1, - одно пустое скобочное выражение,

мы приходим к алгоритму сложности O(n²).

ДРУГОЕ РЕШЕНИЕ этой задачи:

Будем изображать знаком / открывающую скобку, а \ - закрывающую. Правильное скобочное выражение (ПСВ) при n=1 будет выглядеть

так:

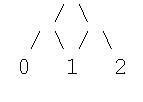
Если мы возьмем картинку

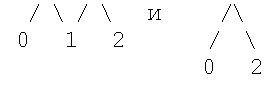
то все ПСВ с n=2 будут такими:

- то есть каждому ПСВ соответствует свой единственный и неповторимый путь между вершинами 0 и 2. Аналогично, все ПСВ с n=3 будут описываться путями в графе

и т.д. Подсчитаем число ПСВ (число путей) при n=3.

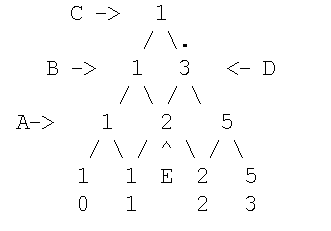
В вершину A мы можем попасть единственным способом - из точки 0, равно в B,C и точку 1 можно попасть, соответственно, только из точек A, B, A. В E можно попасть как из 1, так и из B, поэтому пометка E есть сумма пометок этих узлов, т.е. 2. В D можно попасть либо из Cи (пометка 1), либо из E (пометка 2), и, следовательно, пометка D=3 и т.д.

Аналогично находим количество ПСВ для любого n.

[Назад]

Один из возможных алгоритмов решения задачи такой:

1. Предположим, что существует текст, дешифровка которого неоднозначна, следовательно, существует и текст минимальной длины, для которого возможны по меньшей мере две разбивки

b[1] b[2]...b[k] = c[1] c[2]...c[m]

на слова множества A. Представляя текст в виде отрезка DE, эти разбивки мы можем изобразить следующим образом

Из того, что текст минимальной длины, следует, что концы слов в разных разбивках не могут лежать на одной вертикали (кроме конца текста), т.к. b[1] <> c[1], то одно из кодовых слов (например b[1]) должно входить в другое в качестве префикса и представляться в виде c[1] = b[1] p[1] , где p[1] - это оставшаяся часть слова (суффикс). Далее, либо p[1] входит в b[2] (b[2] =p[1] p[2]), либо b[2] входит в p[1] (p[1] = b[2] p[1] ) в качестве префикса. Определяем новый суффикс p[2]. Продолжая выделять префиксы и суффиксы, получаем, что на каком-то шаге p[j] совпадет с одним из кодовых слов.

Эти рассуждения являются основой следующего алгоритма :

На нулевом шаге возьмем все пары (a[i], a[j]), i <> j, таких кодовых слов, что одно из них есть префикс другого, и найдем все суффиксы p[0,k].

На j-ом шаге для всех пар (p[j-1,k], a[i]), где одно из слов является префиксом другого, опять находим все суффиксы, и те из них, которые не появлялись на предыдущих шагах алгоритма, обозначим p[j,k].

Эти шаги повторяем либо до тех пор, пока какой-либо суффикс не совпадет с одним из кодовых слов (и тогда существует неоднозначно декодируемый текст), либо пока на очередном шаге не появится ни одного нового суффикса (и тогда для любого текста существует единственная дешифровка).

Т.к. количество кодовых слов ограничено, то и суффиксов также конечное число, и на каком-то шаге алгоритм обязательно остановится.

Этот алгоритм принадлежит в первоначальном варианте A. Сардинасу и Дж. Паттерсону (см. Кибернетический сборник, вып.3 стр. 93102 ).

2. Если существует текст, который, используя A, дешифруется неоднозначно, то начинаем выбрасывать из A слова и их комбинации, пытаясь получить множество A' с максимальным числом слов такое, что все тексты, составленные из слов A' дешифруются однозначно.

Сначала из A удаляем i-ое слово , i = 1, 2, ... , n, и делаем проверку по пункту 1. Если удалением одного слова из A мы не получаем искомого множества A', то тогда генерируем все сочетания по n-2 слова из множества A, и для каждого полученного множества делаем проверку по пункту 1, и т.д.

Воспользуемся следующим алгоритмом генерации сочетаний по i слов из множества A:

В массиве B будут находиться индексы используемых на данном шаге элементов из A (общее их число i). В качестве начальной конфигурацией возьмем следующую: B[j]=j, j=1,...,n.

Ищем B[j] с максимальным индексом j такое,что B[j]<n+j-i, увеличиваем это B[j] на 1, а для всех k>j полагаем B[k]=B[k-1]+1 (B[j] растут с ростом j, и мы ищем и увеличиваем на 1 такое B[j] с максимальным номером j, чтобы при заполнении возрастающими значениями элементов массива B[k], k>j, последний элемент B[i] не превосходил бы n). Если такого B[j] не существует, то генерация сочетаний для данного i закончена.

Начинаем генерацию с i=n-1 и проводим ее с уменьшением i до тех пор, пока либо i не станет равно 1 (тогда A' состоит из единственного слова), либо пока проверка по пункту 1 не даст однозначности декодировки.

3. Этот пункт реализуется следующим рекурсивным алгоритмом поиска с возвращением (все слова массива A упорядочены по номерам):

Если ни одно из а[i] не входит в качестве префикса в дешифруемую сейчас строку, то осуществляем возврат на пункт а), предварительно добавляя в начало строки последнее удаленное оттуда слово, и пытаемся выделить из текста слово с большим номером в A. Если возврат осуществить невозможно (т. к. мы находимся в начале исходной строки), то алгоритм заканчивает свою работу. Все возможные дешифровки найдены.

Задача 1. Докажите следующую теорему (Марков А. А.):

Для однозначности декодировки текста достаточно выполнения одного из двух следующих условий:

1) не существует ни одной пары кодовых слов (a[i], a[j]), i<>j, такой, что одно из этих слов есть префикс другого.

2) не существует ни одной пары кодовых слов (a[i], a[j]), i<>j, такой, что одно из них есть суффикс другого.

Задача 2. Приведите пример такого множества кодовых слов, что для него не выполняется ни условие 1, ни условие 2 из предыдущего пункта, а декодировка любого текста, составленного при помощи этоих слов - однозначная.

[Назад]

Обратите внимание на то, что от посылки сигнала на интерфейс до приема сигнала должно пройти некоторое время. В программе необходимо учесть возникновение этой паузы.

[Назад]

Чтобы суммы меток ребер при вершинах были равны, необходимо, чтобы эта сумма равнялась 2*(1+2+...+12)/8, так как каждому ребру смежны 2 вершины (т.е. оно подсчитывается дважды), а количество вершин - 8. Но число 2*(1+2+...+12)/8=2*12*13/(2*8) - не целое. Поэтому нумерации не существует.

[Назад]

Полное описание решения этой задачи можно найти в журнале

"Информатика и образование" N 5-6 за 1992 г.

[Назад]

        l:=0; r:=n;
        {инвариант: a[1]..a[l]<=b; a[r+1]..a[n]>=b}
        while l <> r do begin
        | if a[l+1] <= b then begin
        | | l:=l+1;
        | end else if a[r]>=b then begin
        | | r:=r-1;
        | end else begin {a[l+1]>b; a[r]<b}
        | | поменять a[l+1] и  a[r]
        | | l:=l+1; r:+r-1;
        | end;
        end;

[Назад]

Потребуются три границы: до первой будут идти элементы, меньшие b, от первой до второй - равные b, затем неизвестно какие до третьей, а после третьей - большие b. (Более симметричное решение использовало бы четыре границы, но вряд ли игра стоит свеч.) В качестве очередного рассматриваемого элемента берем элемент справа от средней границы.

     l:=0; m:=0; r:=n;
     {инвариант: a[1..l]<b; a[l+1..m]=b; a[r+1]..a[n]>b}
     while m <> r do begin
     | if a[m+1]=b then begin
     | | m:=m+1;
     | end else if a[m+1]>b then begin
     | | обменять a[m+1] и a[r]
     | | r:=r-1;
     | end else begin {a[m+1]<b}
     | | обменять a[m+1] и a[l+1]
     | | l:=l+1; m:=m+1;
     end;

[Назад]

Вверх по странице, к оглавлению и навигации.