 |
Используемая терминология.
Граф.
На пальцах...
Вообще говоря, граф - система точек и связывающих их отрезков. Иногда отрезкам приписаны направления. Тогда граф называется ориентированным, а отрезки изображаются стрелочками. Циклы в этом случае - пути из вершины-точки в себя по ребрам-стрелкам в указанном направлении.
Иногда ребрам приписаны цены(веса) - некоторые числа, которые могут характеризовать, например, стоимость пути из одной вершины в другую. Такие цены обычно хранятся в матрице A, где aij - цена пути из вершины i в вершину j.
Математическое определение.
Графом G называется пара множеств G = {V, E} V - вершин, E - дуг и отображение Г: E --> V * V сопоставляющее каждой дуге e из E пару вершин (v,w) - начало и конец дуги.
Иногда начало и конец дуги не различают, называя их просто концами. В таком случае граф называют неориентированным, а дугу - ребром. v,w называются смежными, если существует e из E такое, что Г(e)=(v,w) или Г(e)=(w,v). В этом случае также говорят, что е и v (e и w) - инцидентны. Отношение смежности или инцидентности полностью характеризуют граф. Локальные свойства вершин графа задаются множествами смежных вершин:
Г(v,-)={ w из V | существует е из Е, е=(v,w) } - множество
концов дуг с началом в v.
Г(v,+)={ w из V | существует е из Е, е=(w,v) } - множество
начал дуг с концом в v.
Соответствующие множества дуг назовем Е(v,-) и E(v,+).
Числа r(v,-) = |Е(v,-)| и r(v,+) = |E(v,+)| - полустепени исхода и захода вершины v, r(v)= r(v,-) + r(v,+) - степень вершины. Вершина v изолирована, если |r(v)| = 0 и называется висящей вершиной или листом графа, если |r(v)| = 1.
Если из Е удалить часть дуг, получится частичный граф исходного графа, при удалении части вершин и всех дуг инцидентных этим вершинам - подграф. Граф называется пустым, если |Е| = 0, (смежных вершин нет), полным, если любые две вершины смежные, граф дополняет исходный, если в нем смежены те и только те вершины, которые не смежные в исходном графе. Граф называется простым или двудольным, если для любой его вершины v из V r(v,-) = 0 или r(v,+) = 0.
Примеры подграфов. Дуги инцидентные одной вершине, вместе с их концами, образуют куст. Другой важный пример. Список вершин {v0, v1, v2, v3, ... , vk} вместе с множеством дуг e1=(v0, v1), e2=(v1, v2), e3=(v2, v3), ... ,e1=(vk-1, vk), содержащихся в Е, составляют k - звенный путь в G , если среди v0, v1, v2, ... , vk - нет одинаковых.
Путь однозначно определяется множеством составляющих его дуг или списком вершин. Вершина v0 называется началом, vk - концом пути. Если в тех же условиях v0 = vk , подграф называется контуром. В неориентированном случае (когда вместо дуги e2=(v1,v2) может присутствовать, e2=(v3, v2) ) эти же конструкции называются цепью и циклом. Цикл из одной дуги называется петлей.
Если снять условие различия v0, v1, ... , vk, то аналогичная конструкция будет называться обходом графа.
Граф называется связным, если любая пара его вершин является концами некоторой цепи этого графа.
Hетрудно показать, что отношение 'две вершины связаны цепью' удовлетворяет всем свойствам отношения эквивалентности и разбивает множества вершин V на непересекающиеся подмножества V1, V2, ... , Vr. Эти подмножества вершин задают разбиение G на компоненты связности - наибольшие связные подграфы.
Конструктивно доказывается следующая теорема. Пусть G = {M, N}
- связный граф. Тогда существует N' - подмножество N, такое, что
1) {V, E'} - связен,
2) | E'| = | V | - 1
3) Существует нумерация p: V ---> 1 : m , q: E' ---> 2 : m
такая, что каждому (w,v) из Е
q( (v,w) ) = MAX { p(v), P(w) }
Этот результат позволяет эффективно реализовать некоторые алгоритмы, а также лежит в основе важного комбинаторного объекта - дерева. Деревом называется граф, который
а) связен.
б) не содержит ни одного цикла.
Дерево также обладает следующими свойствами:в) число дуг дерева на единицу меньше числа вершин.
г) при удалении любой дуги этот граф теряет связность.
д) при добавлении любой дуги в этом графе появляется цикл (такой цикл называют основным).
е) любые две вершины этого графа связаны единственной цепью.
Свойства г) и д) характеризуют этот граф как экстремальный (минимальный связный и максимальный без циклов на заданном множестве вершин) свойство е) лежит в основе обоснования корректности некоторых важных вычислительных алгоритмов.
Дерево характеризуется следующими наборами перечисленных свойств: а),б) (определение) <=> а),в) <=> б),в) <=> а),г) <=> б),д) <=> е).
Hекоторую произвольно выбранную вершину дерева v0 иногда называют его корнем. Тогда уровень любой вершины дерева определяется как число звеньев цепи, соединяющей ее с корнем.
Вершина w потомок v, если v лежит на пути соединяющем w и v0, и непосредственный потомок v, если уровень w равен уровню v + 1. Понятие, обратное к отношению потомка - предок вершины всегда только один. Дерево назовем иерархическим, если любая цепь с началом в вершине v0 обязательно яляется путем (все дуги ориентированы от корневой). Дерево называется двоичным (бинарным), если каждая вершина имеет не более двух потомков.
Сетью называют граф, дугам и (или) вершинам которого при- писаны числовые параметры.
Метрика.
Метрика задается функцией d с следующими свойствами:
| Неотрицательность |
d(x,y) > 0 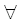 x,y x,y |
(1) |
| Свойство нуля | d(x,y) = 0 <=> x=y | (2) |
| Симметричность | d(x,y) = d(y,x) 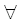 x,y x,y |
(3) |
| Неравенство треугольника | d(x,z) < d(x,y) + d(y,z) 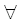 x,y,z x,y,z |
(4) |
Последовательности длины n иногда объявляют векторами в Rn и применяют обычные расстояния: 'шахматной доски' maxi |xi-yi|, 'сити-блок' ('городских кварталов') 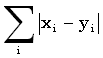 и Евклида
и Евклида 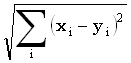 .
.
 Вверх по странице, к оглавлению и навигации.
Вверх по странице, к оглавлению и навигации.