|
|
| Обозначение |
 |
| Область значений |
 |
| Параметры | Параметр формы a > 0 |
| Плотность |
|
| Функция распределения | Не выражается в элементарных функциях |
Если 
~
, i=1,2, то 
~
.
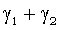Если ~, i=1,2, то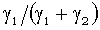 
~
.
Если 0 < a <1, возьмем три независимых случайных числа r1, r2, r3, равномерно распределенных на отрезке [0,1]. Положим 
, 
. Если s1+s2>1, то возьмем вместо r1, r2 другую пару таких же случайных чисел. Так будем поступать до тех пор, пока не получим 
. В этом случае зададим y, x1 и x2 следующими соотношениями:
y=s1/(s1+s2)
, x1 = -y ln(r3), x2 = -(1-y) ln(r3).Случайные числа x1 и x2 независимы и распределены как и 
соответственно.
Для значений параметра, больших единицы, можно дополнить этот метод, воспользовавшись свойством аддитивности.
Легко получить степенные ряды, позволяющие вычислять гамма-распределение (cм. Абрамовиц, Стиган [6.5.29]):
,
.
Как обычно, второй ряд – из-за положительности членов – ведет себя с вычислительной точки зрения лучше первого. Но с ростом x скорость сходимости степенного ряда довольно быстро падает. Зато с ростом x растет скорость сходимости цепной дроби (cм. Абрамовиц, Стиган [6.5.31]):
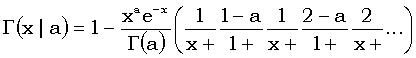
И снова подпоследовательность ее четных подходящих дробей монотонно сходится к нужному значению.
Численные эксперименты показывают, что для x, меньших a, лучше использовать степенной ряд, а для больших – цепную дробь. Оказывается, когда x примерно равняется
a, требуется просуммировать около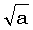 
членов ряда, причем с уменьшением x число требуемых членов ряда быстро убывает. Аналогично ведет себя цепная дробь при 
.
В большинстве статистических пакетов (в частности, в широко распространенных в России пакетах Statistica и SPSS) функция гамма-распределения зависит от двух параметров, которые принято называть форма (shape) и масштаб (scale). Пусть a – параметр формы, b – параметр масштаба; для функции гамма-распределения будем использовать обозначение 
. Формула для плотности выглядит в этом случае следующим образом:
Внимание: иногда в качестве параметра формы используется 
.
В приведенных ниже кодах предлагается именно этот вариант, ставший де-факто стандартом в прикладной статистике. По умолчанию параметр масштаба равен 1, этот случай соответствует рассмотренному в "основном" тексте. Приводимые коды следует, естественно, рассматривать лишь как иллюстрацию, хотя и работоспособную во всех статистических задачах, с которым я сталкивался.
Для работы с этими кодами необходимо уметь вычислять гамма-функцию (см. Приложение А и файлы loggamma.h и loggamma.cpp).
/***********************************************************/
/* Gamma distribution */
/***********************************************************/
#ifndef __GAMMA_H__ /* To prevent redefinition */
#define ENTRY extern
#define LOCAL static
class GammaDF {
public:
GammaDF(double shape, double scale=1);
double value(double x); // Функция распределения Gamma(x|shape,scale)
double inv(double p); // Обратная функция: Gamma(x|shape,scale)=p
private:
double a, shape, scale, lga;
double fraction(double x);
double series(double x);
};
#define __GAMMA_H__ /* Prevents redefinition */
#endif /* Ends #ifndef __GAMMA_H__ */
|
/***********************************************************/
/* Гамма-распределение */
/***********************************************************/
#include <math.h>
#include <assert.h>
#include "gammaDF.h"
#include "logGamma.h"
LOCAL const double zero = 0.0;
LOCAL const double one = 1.0;
LOCAL const double two = 2.0;
GammaDF::GammaDF(double shape, double scale):
a(shape), shape(shape), scale(scale), lga(logGamma(shape))
{
assert(shape > 0 && scale > 0);
}
double
GammaDF::series(double x)
// См. Abramowitz & Stegun,
// Handbook of Mathematical Functions, 1964 [6.5.29]
// М.Абрамовиц, И.Стиган
// Справочник по специальным функциям (М: Мир, 1979)
//
// Для вычисления неполной гамма функции P(a,x)
// используется ее разложение в ряд Тейлора.
//
{
double sum, prev_sum, term, aa = a;
long i = 0;
term = sum = one / a;
do {
aa += one;
term *= x / aa;
prev_sum = sum; sum += term;
i++;
} while(fabs(prev_sum) != fabs(sum));
return sum *= exp(-x + a * log(x) - lga);
}/* incGamma_series */
double
GammaDF::fraction(double x)
// См. Abramowitz & Stegun,
// Handbook of Mathematical Functions, 1964 [6.5.31]
// М.Абрамовиц, И.Стиган
// Справочник по специальным функциям (М: Мир, 1979)
//
// Для вычисления неполной гамма функции P(a,x)
// используется ее разложение в цепную дробь Лежандра
//
// P(a,x)=exp(-x +x*ln(a))*CF/logGamma(a),
//
// где
//
// 1 1-a 1 2-a 2
// CF = --- ----- --- ----- --- ....
// x+ 1+ x+ 1+ x+
//
// Используются подходящие дроби CF(n) = A(n) / B(n)
//
// где
// A(n) = (s(n) * A(n-1) + r(n) * A(n-2)) * factor
// B(n) = (s(n) * B(n-1) + r(n) * B(n-2)) * factor
// причем
// A(-1) = 1, B(-1) = 0, A(0) = s(0), B(0) = 1.
//
// Здесь
//
// s(0) = 0, s(1) = x, r(0) = 0, r(1) = 1,
//
// так что
//
// A(1) = one * factor, B(1) = r * factor
//
// и, следовательно,
//
// r(i) = k - a if i = 2k, k > 0
// r(i) = k if i = 2k+1,
// s(i) = 1 if i = 2k,
// s(i) = x if i = 2k+1
//
// factor - шкалирующий множитель
//
{
double old_sum=zero, factor=one;
double A0=zero, A1=one, B0=one, B1=x;
double sum=one/x, z=zero, ma=zero-a, rfact;
do {
z += one;
ma += one;
/* two steps of recurrence replace A's & B's */
A0 = (A1 + ma * A0) * factor; /* i even */
B0 = (B1 + ma * B0) * factor;
rfact = z * factor;
A1 = x * A0 + rfact * A1; /* i odd, A0 already rescaled */
B1 = x * B0 + rfact * B1;
if (B1) {
factor = one / B1;
old_sum = sum;
sum = A1 * factor;
}/* if */
} while (fabs(sum) != fabs(old_sum));
return exp(-x + a * log(x) - lga) * sum;
}/*fraction*/
double
GammaDF::value(double x)
// Вычисляется Gamma(x|a):
// вероятность того, что случайная величина,
// подчиняющаяся центральному гамма-распределению с параметром 'a',
// меньше или равна 'x'.
{
x *= scale;
if(x <= zero)
return zero; /* НЕ ошибка! */
else if(x < (a + one))
return series(x);
else
return one - fraction(x);
}/*value*/
double
GammaDF::inv(double p)
// Ищет такое значение 'x', для которого Gamma(x|a) = p,
// т.е. равна 'p' вероятность того, что случайная величина,
// подчиняющаяся центральному гамма-распределению с параметром 'a',
// меньше или равна 'x'.
{
double fx, l = 0, r = 1, x;
if (p == 0) return 0;
assert(p > 0 && p < 1);
for(l=0, r=a/2; value(r) < p; r+=a/2) l=r;
x=(l+r)/2;
do {
fx = value(x);
if (fx > p) r = x; else
if (fx < p) l = x; else
break;
x = (l + r)* 0.5;
} while ((l!=x) && (r!=x));
return x;
}/*inv*/
|
|
|
Дата последней модификации: 25 октября 2000 г.
, где 
– (полная) гамма-функция от параметра a.