 |
Cтруктуры данных. Хранение информации.
Рекурсивные структуры данных: общие сведения.
© Кантор И.
Основа всех подобных структур - список. Объявим его элемент следующим образом:
typedef struct list_ {
int data; // Место для данных, естественно, не всегда int.
struct list_ *next; // Указатель на такой же элемент (или на NULL)
} list;
Cоздадим такой элемент и проинициализуем его:list *OurList; OurList = (list *)malloc(sizeof(list)); Ourlist->data = 123; // Данные, естественно, могут быть любые Ourlist->next = NULL; // На NULL всегда указывает только последний в списке
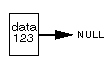 |
Появился элемент данных, содержащий указатель на элемент того же типа (пока еще он пустой: NULL). |
Теперь мы можем добавить еще один элемент за ним:
OurList -> next = (list *)malloc(sizeof(list));
И, при необходимости, переместить его вперед:
OurList -> next -> next = OurList; // 'разворачиваем' новый элемент OurList -> next = NULL; // А теперь - старый
Такие операции могут иметь свои нюансы, но, поняв устройство структуры, вы легко составите нужный алгоритм. Обычно что-то странное может быть с первым и последним элементом нашего 'паровозного состава'.
Один элемент в списке всегда указывает на NULL - чтобы циклу, перебирающему элементы списка, или другой программе было видно, где конец списка (ведущий элемент 'поезда').

Предполагая, что X и P являются указателями, число 18 можно вставить в такой список следующим образом:
X->Next = P->Next; P->Next = X;
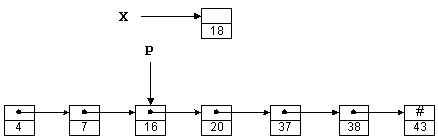
Вначалe вы можете создать указатель last_vagon, указывающий на начальный элемент списка (последний в 'поезде'), и далее 'продвигаться по вагонам' при создании новых элементов или поиске нужных.
Создание и инициализация списка.
last_vagon = OurList;
while ( Требуется создать элемент списка )
{
// Переходим к следующему вагону.
OurList = Ourlist -> next;
// инициализация элемента
OurList = (list *)malloc(sizeof(list));
Заполнить данными ( OurList );
}
// Конец указывает на NULL
OurList -> next = NULL;
...
Начало не потеряно - есть указатель last_vagon ! От него мы можем добраться до любого элемента списка.
Таким образом мы можем сохранять указатели на любые фиксированные элементы. Обычно их нужно 1-2 штуки кроме основного.
Очевидно, возможна реализация, когда каждый новый элемент добавляется с другого конца списка - в этом случае
// Прибавление к списку с левого конца элемента NewElem temp = OurList; NewElem -> next = OurList; // OurList будет всегда указывать на конец состава. OurList = new; ...
Пример функции, последовательно обрабатывающей все элементы, следующие за OurList.
last_vagon = OurList;
while ( OurList -> next != NULL )
{
// Переходим к следующему вагону.
OurList = Ourlist -> next;
Обработать (OurList);
}
// OurList теперь указывает на правый конец списка.
// Начало не потеряно: есть указатель last_vagon !
// От него мы cможем добраться до любого элемента списка.
...
Списки бывают односвязные - как описано и двусвязные - с указателями в обе стороны.
Мы можем создавать свои функции для работы со списками и менять сами списки для обеспечения максимального удобства.
Перечислю стандартные реализации (которые, естественно, могут быть выполнены и на массивах):
-
Очередь - список со следующими операциями:
- Проверку непустоты списка.
- Добавление дополнительного элемента s, следующего за последним в очереди. При этом s становится последним.
- Извлечение из очереди первого элемента с записью его в s. Первым при этом становится элемент, непосредственно следующий за s.
- Проверку непустоты списка.
-
Стек - нечто вроде столбика из кирпичей - каждый следующий кладется 'поверх' предыдущих, в начало списка. Стеком назовем список S , допускающий три операции:
-
Проверку непустоты списка.
- Добавление дополнительного элемента s, следующего за последним в Стеке. При этом s становится последним.
- Извлечение из S последнего элемента с записью его в s. Последним при этом становится элемент, непосредственно предшествующий s.
Дек - комбинированная структура. Есть доступ и к концу и к началу списка. Реализованы операции и очереди и стека.
Кольцо - первый элемент указывает на последний.
-
Проверку непустоты списка.
-
Дерево: у дерева есть корень - нулевой уровень, от которого идет в случае бинарного дерева - не более двух ссылок на поддеревья, в случае тернарного - не более трех ссылок, а в случае бора - сколько потребуется. Элементы, от которых ссылок нет - 'листья'.
уровень: 0 | 0 - корень | /|\ | / | \ | / | \ 1 | 1 2 3 | /| |\ | / | | \ 2 |4 5 6 7 | \ | \ 3 | 8 Бинарное дерево.
Чем хороши/плохи структуры, основанные на списках ?
В первую очередь по сравнению с массивом:Плюсы:
- Динамические вставка и удаление.
Памяти выделяется всегда сколько нужно. Массив же инициализуется один раз.
- Возможность вставки элемента между
В массиве такое почти не реально или чрезвычайно медленно и неэффективно.
- Память тратится на указатели
Часто такие затраты незначительны, по сравнению с данными, однако имеют место.
- Нет мгновенного доступа к элементам
В обычном списке элемент можно найти за O(n) операций.
Cписки в чистом виде используются редко, они - инструмент для организации словарей - удобных структур хранения информации с быстрой вставкой/поиском и удалением элементов.
 Вверх по странице, к оглавлению и навигации.
Вверх по странице, к оглавлению и навигации.