| В этой
главе рассмотрим ещё один приём перечисления всех элементов некоторого
множества. Его называют ╚поиск с возвратами╩, ╚метод ветвей и границ╩ или
╚обход дерева╩.
Перед изучением темы необходимо познакомиться с понятиями: граф, дерево - связный граф с минимальным числом рёбер. Обход дерева. Перебор с возвратами. Во многих книгах
приводятся головоломки, интересные тем, что для их решения не требуется
особых математических или каких-либо других специальных научных знаний.
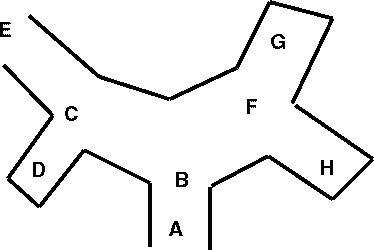
К таким задачам относятся поиск пути в сложном лабиринте, чтение текста
ходом шахматного коня, расстановка фигур на шахматной доске таким образом,
чтобы удовлетворить известным условиям.
Из пункта А мы попадаем в пункт В, из В - в С, из С - в D. Отсюда дороги нет. Мы снова возвращаемся на ближайший ╚перекресток╩ С и из него пробуем пройти по новой дороге в пункт Е. Здесь мы обнаруживаем выход. Задача решена. Её решение - путь АВСЕ. Заметим, узнав, что мы пошли неверным путем, мы не начинаем решать задачу заново, а делаем лишь один шаг назад и снова пытаемся идти с этого места. Если , сделав шаг назад, обнаруживаем, что нет новых неисследованных путей, делаем назад ещё один шаг и т.д. до тех пор, пока мы не доходим до места, из которого можно пойти новым, не испробованным путем. Если возвращаясь, мы дошли до исходной точки и из нее нет новых путей, то задача не имеет решения. Решая любую
задачу по программированию требуется сначала создать математическую модель.
В задаче, которую мы будем рассматривать, такой моделью является дерево.
Дерево это частный случай графа.
В подобных задачах полезно рассмотреть частный случай (с фиксированным малым количеством переменных), на основе частного случая составить алгоритм и обобщить его на n переменных. Задача о
восьми ферзях - хорошо известный пример использования метода перебора
с возвратом. В 1850 г. Эту задачу исследовал К.Ф.Гаусс, однако полностью
он её так и не решил, т.к. для подобных задач характерно отсутствие аналитического
решения. Они требуют огромного количества изнурительной работы.
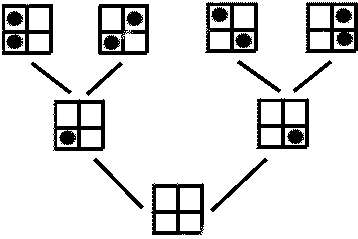
Нарисуем ⌠дерево
позиций■: его корнем будет единственная 0-позиция, а из каждой k-позиции
выходит n стрелок вверх в (k+1)-позиции. Эти n позиций отличаются положением
ферзя на (k+1)-ой горизонтали. Будем считать, что расположение их на рисунке
соответствует положению этого ферзя: левее та позиция, в которой
ферзь расположен левее.
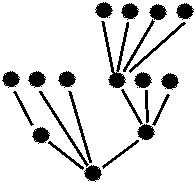
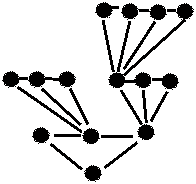
Точнее, назовем k-позицию допустимой, если после удаления верхнего ферзя оставшиеся не бьют друг друга. Наша программа будет рассматривать только допустимые позиции. 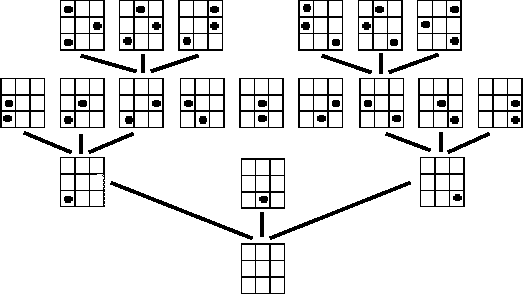 Разобьем задачу на две части: (1) обход произвольного дерева и (2) реализацию дерева допустимы позиций. Сформулируем задачу обхода произвольного дерева. Будем считать, что у нас имеется робот, который в каждый момент находится в одной из вершин дерева (вершины изображены на рисунке кружочками). Он умеет выполнять команды:
Доказательство правильности приводимой далее программы использует такие определения. Пусть фиксировано положение Робота в одной из вершин дерева, тогда все листья дерева разбиваются на три категории: над Роботом, левее Робота, и правее Робота. (Путь из корня в лист может проходить через вершину с Роботом, сворачивать влево, не доходя до нее и сворачивать вправо, не доходя до нее.) Через (ОЛ) обозначим условие ⌠обработаны все листья левее Робота■, а через (ОЛН) ≈ условие ⌠обработаны все листья левее и над Роботом■.
Левее Над Правее
procedure вверх_до_упора_и_обработатьОсновной алгоритм: дано: Робот в корне, листья не обработаныОсталось воспользоваться следующими свойствами команд Робота (в каждой строке в первой фигурной скобке записаны условия, в которых выполняется команда, во второй ≈ утверждения о результате ее выполнения): (1) {ОЛ, не есть_сверху} обработать {ОЛН}Реализуем операции с деревом позиций. Позицию будем представлять с помощью переменной k: 0..n (число ферзей) и массива c: array [1..n] of 1..n ( c[i] - координаты ферзя на i-ой горизонтали). Предполагается, что все позиции допустимы (если убрать верхнего ферзя, остальные не бьют друг друга). const n=...;Литература: 1. Н.Я.Виленкин. Комбинаторика.Упражнения: 1. Приведенная программа тратит довольно много времени на выполнение проверки есть_сверху (проверка, находится ли верхний ферзь под боем, требует числа действий порядка n ). Изменить реализацию операций с деревом позиций так, чтобы все три проверки есть_сверху / справа / снизу и соответствующие команды требовали бы количества действий, ограниченного не зависящей от n константой. |