Напомним, что наша основная цель -- это поиск вывода заданного слова, или, другими словами, поиск успешного LR-процесса над ним. Во всех рассматриваемых нами грамматиках успешный LR-процесс (над данным словом) единствен. Искать этот единственный успешный процесс мы будем постепенно: в каждый момент мы смотрим, какой шаг возможен следующим. Для этого на грамматику надо наложить дополнительные требования, и сейчас мы рассмотрим простейший случай так называемых LR(0)-грамматик. Мы уже знаем:
(1) В успешном LR-процессе возможна свертка по правилуАналогичное утверждение про сдвиг гласит:при содержимом стека S тогда и только тогда, когда S принадлежит
или, другими словами, когда слово S согласовано с ситуацией
.
(2) В успешном LR-процессе при содержимом стека S возможен сдвиг с очередным символом a тогда и только тогда, когда S согласовано с некоторой ситуацией.
![]() 14.2.1. Докажите это.
14.2.1. Докажите это.
Рассмотрим некоторую грамматику и произвольное
слово S из терминалов и нетерминалов. Если множество
![]() содержит ситуацию, в которой справа от
подчеркивания стоит терминал, то говорят, что для слова
S возможен сдвиг. Если в
содержит ситуацию, в которой справа от
подчеркивания стоит терминал, то говорят, что для слова
S возможен сдвиг. Если в ![]() есть ситуация, в
которой справа от подчеркивания ничего нет, то говорят, что
для слова S возможна свертка (по соответствующему
правилу). Говорят, что для слова S возникает конфликт
типа сдвиг/свертка, если возможны и сдвиг, и свертка. Говорят,
что для слова S возникает конфликт типа свертка/свертка,
если есть несколько правил, по которым возможна свертка.
есть ситуация, в
которой справа от подчеркивания ничего нет, то говорят, что
для слова S возможна свертка (по соответствующему
правилу). Говорят, что для слова S возникает конфликт
типа сдвиг/свертка, если возможны и сдвиг, и свертка. Говорят,
что для слова S возникает конфликт типа свертка/свертка,
если есть несколько правил, по которым возможна свертка.
Грамматика называется LR(0)-грамматикой, если в ней нет конфликтов типа сдвиг/свертка и свертка/свертка ни для одного слова S.
![]() 14.2.2. Является ли приведенная выше грамматика
LR(0)-грамматикой?
14.2.2. Является ли приведенная выше грамматика
LR(0)-грамматикой?
![]() 14.2.3. Являются ли LR(0)-грамматиками такие:
14.2.3. Являются ли LR(0)-грамматиками такие:
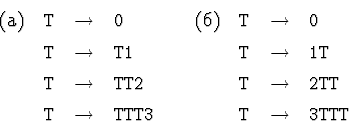 Решение. Являются, см. соответствующие таблицы (конфликтов
нет).
Решение. Являются, см. соответствующие таблицы (конфликтов
нет).



Эта задача показывает, что LR(0)-грамматики могут быть как леворекурсивными, так и праворекурсивными.
![]() 14.2.4. Пусть дана LR(0)-грамматика. Доказать, что у любого слова
существует не более одного правого вывода. Построить алгоритм
проверки выводимости в LR(0)-грамматике.
14.2.4. Пусть дана LR(0)-грамматика. Доказать, что у любого слова
существует не более одного правого вывода. Построить алгоритм
проверки выводимости в LR(0)-грамматике.
![]() 14.2.5. Что произойдет, если анализируемое слово не имеет
вывода в данной грамматике?
14.2.5. Что произойдет, если анализируемое слово не имеет
вывода в данной грамматике?
Замечания. 1. При реализации этого алгоритма нет
необходимости каждый раз заново вычислять множество
![]() для текущего значения S. Эти множества
можно также хранить в стеке (в каждый момент хранятся множества
для текущего значения S. Эти множества
можно также хранить в стеке (в каждый момент хранятся множества
 для всех начал T текущего слова S).
для всех начал T текущего слова S).
2. На самом деле само слово S можно не хранить --
достаточно хранить множества ситуаций  для всех
его начал T (включая само S).
для всех
его начал T (включая само S).
В алгоритме проверки выводимости в LR(0)-грамматике мы используем не всю информацию, которую могли бы. В этом алгоритме для каждого состояния известно заранее, что в нем возможен только сдвиг или только свертка (причем в последнем случае известно, по какому правилу). Более изощренный алгоритм мог бы принимать решение о выборе между сдвигом и сверткой, посмотрев на очередной символ (Next). Глядя на состояние, можно сказать, при каких значениях Next возможен сдвиг (это те терминалы, которые в ситуациях этого состояния стоят непосредственно за подчеркиванием). Сложнее воспользоваться информацией о символе Next для решения вопроса о том, возможна ли свертка. Для этого есть упрощенный метод (грамматики, к которым он применим, называют SLR(1)-грамматиками [сокращение от Simple LR(1)]) и полный метод (более сложный, но использующий всю возможную информацию; грамматики, к которым он применим, называют LR(1)-грамматиками). Есть и промежуточный класс грамматик, называемый LALR(1).