![]() 2.3.1. Перечислить все k-элементные подмножества множества
1..n.
2.3.1. Перечислить все k-элементные подмножества множества
1..n.
В каком случае s-ый член последовательности можно увеличить, не меняя предыдущие? Если x[s] меняется с 0 на 1, то для сохранения общего числа единиц нужно справа от х[s] заменить 1 на 0. Для этого надо, чтобы справа от x[s] единицы были. Если мы хотим перейти к непосредственно следующему, то x[s] должен быть первым справа нулем, за которым стоят единицы. Легко видеть, что х[s+1]=1 (иначе х[s] не первый). Таким образом надо искать наибольшее s, для которого х[s]=0, x[s+1]=1:
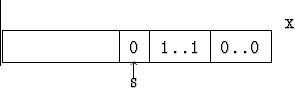
За х[s+1] могут идти еще несколько единиц, а после них несколько нулей. Заменив х[s] на 1, надо выбрать идущие за ним члены так, чтобы последовательность была бы минимальна с точки зрения нашего порядка, т.е. чтобы сначала шли нули, а потом единицы. Вот что получается:
первая последовательность: 0..01..1 (n-k нулей, k единиц)
последняя последовательность: 1..10..0 (k единиц, n-k нулей)
алгоритм перехода к следующей за х[1]..x[n] последовательности (предполагаем, что она есть):
s := n - 1;
while not ((x[s]=0) and (x[s+1]=1)) do begin
| s := s - 1;
end;
{s - член, подлежащий изменению с 0 на 1}
num:=0;
for k := s to n do begin
| num := num + x[k];
end;
{num - число единиц на участке x[s]...x[n],
число нулей равно (длина - число единиц),
т. е. (n-s+1) - num}
x[s]:=1;
for k := s+1 to n-num+1 do begin
| x[k] := 0;
end;
{осталось поместить num-1 единиц в конце}
for k := n-num+2 to n do begin
| x[k]:=1;
end;`
Другой способ представления подмножеств -- это перечисление их элементов. Чтобы каждое подмножество имело ровно одно представление, договоримся перечислять элементы в возрастающем порядке. Приходим к такой задаче.
![]() 2.3.2. Перечислить все возрастающие последовательности
длины k из чисел 1..n в лексикографическом
порядке. (Пример: при n=5, k=2 получаем:
12 13 14 15 23 24 25 34
35 45.)
2.3.2. Перечислить все возрастающие последовательности
длины k из чисел 1..n в лексикографическом
порядке. (Пример: при n=5, k=2 получаем:
12 13 14 15 23 24 25 34
35 45.)
s:=n;
while not (x[s] < n-k+s) do begin
| s:=s-1;
end;
{s - номер элемента, подлежащего увеличению};
x[s] := x[s]+1;
for i := s+1 to n do begin
| x[i] := x[i-1]+1;
end;`
![]() 2.3.3. Пусть мы решили представлять k-элементные
подмножества множества 1..n убывающими последовательностями
длины k, упорядоченными по-прежнему лексикографически.
(Пример:
21 31 32 41 42 43 51 52 53 54.) Как выглядит тогда алгоритм
перехода к следующей?
2.3.3. Пусть мы решили представлять k-элементные
подмножества множества 1..n убывающими последовательностями
длины k, упорядоченными по-прежнему лексикографически.
(Пример:
21 31 32 41 42 43 51 52 53 54.) Как выглядит тогда алгоритм
перехода к следующей?
![]() 2.3.4. Решить две предыдущие задачи, заменив
лексикографический порядок на обратный (раньше идут те, которые
больше в лексикографическом порядке).
2.3.4. Решить две предыдущие задачи, заменив
лексикографический порядок на обратный (раньше идут те, которые
больше в лексикографическом порядке).![]()
![]() 2.3.5. Перечислить все вложения (функции, переводящие
разные элементы в разные) множества 1..k в
1..n
(предполагается, что k
2.3.5. Перечислить все вложения (функции, переводящие
разные элементы в разные) множества 1..k в
1..n
(предполагается, что k![]() n). Порождение очередного элемента
должно требовать не более C
n). Порождение очередного элемента
должно требовать не более C![]() k действий.
k действий.