Чтобы определить то, что называют контекстно-свободной грамматикой (КС-грамматикой), надо:
Пусть фиксирована КС-грамматика (мы часто будем опускать
приставку << КС->>, так как других грамматик у нас не будет).
Выводом в этой грамматике называется последовательность слов
![]() , в которой X0 состоит из одного символа,
и этот символ -- начальный, а Xi+1 получается из Xi заменой
некоторого нетерминального символа K на слово X по одному из
правил грамматики. Слово, составленное из терминальных символов,
называется выводимым, если существует вывод, который им
кончается. Множество всех выводимых слов (из терминальных
символов) называется языком, порождаемым данной грамматикой.
, в которой X0 состоит из одного символа,
и этот символ -- начальный, а Xi+1 получается из Xi заменой
некоторого нетерминального символа K на слово X по одному из
правил грамматики. Слово, составленное из терминальных символов,
называется выводимым, если существует вывод, который им
кончается. Множество всех выводимых слов (из терминальных
символов) называется языком, порождаемым данной грамматикой.
В этой и следующей главе нас будет интересовать такой вопрос: дана КС-грамматика; построить алгоритм, который по любому слову проверяет, выводимо ли оно в этой грамматике.
![\begin{eqnarray*}
\mbox{\tt E} & \to & \mbox{\tt (E)}\\ \mbox{\tt E} & \to & \m...
...E]}\\ \mbox{\tt E} & \to & \mbox{\tt EE}\\ \mbox{\tt E} & \to &\end{eqnarray*}](img551.gif) (в последнем правиле справа стоит пустое слово).
(в последнем правиле справа стоит пустое слово).
Примеры выводимых слов:
Пример 2. Другая грамматика, порождающая тот же язык: Алфавит: ( ) [ ] T E
Правила:
![\begin{eqnarray*}
\mbox{\tt E} &\to&\\ \mbox{\tt E} &\to&\mbox{\tt TE}\\ \mbox{\tt T} &\to&\mbox{\tt (E)}\\ \mbox{\tt T} &\to&\mbox{\tt [E]}\end{eqnarray*}](img553.gif) Начальным символом во всех приводимых далее примерах будем
считать символ, стоящий в левой части первого правила (в данном
случае это символ E), не оговаривая этого особо.
Начальным символом во всех приводимых далее примерах будем
считать символ, стоящий в левой части первого правила (в данном
случае это символ E), не оговаривая этого особо.
Для каждого нетерминального символа можно рассмотреть множество всех слов из терминальных символов, которые из него выводятся (аналогично тому, как это сделано для начального символа в определении выводимости в грамматике). Каждое правило грамматики можно рассматривать как свойство этих множеств. Покажем это на примере только что приведенной грамматики. Пусть T и E -- множества слов (из скобок), выводимых из нетерминалов T и E соответственно. Тогда правилам грамматики соответствуют такие свойства:
=10000

Сформулированные свойства множеств E , T не определяют эти множества однозначно (например, они остаются верными, если в качестве E и T взять множество всех слов). Однако можно доказать, что множества, задаваемые грамматикой, являются минимальными среди удовлетворяющих этим условиям.
![]() 13.1.1. Сформулируйте точно и докажите это утверждение для
произвольной контекстно-свободной грамматики.
13.1.1. Сформулируйте точно и докажите это утверждение для
произвольной контекстно-свободной грамматики.![]()
![]() 13.1.2. Постройте грамматику, в которой выводимы слова
13.1.2. Постройте грамматику, в которой выводимы слова
(а) 00..0011..11 (число нулей равно числу единиц);
(б) 00..0011..11 (число нулей вдвое больше числа единиц);
(в) 00..0011..11 (число нулей больше числа единиц);
(и только они).![]()
![]() 13.1.3. Доказать, что не существует КС-грамматики, в которой
были бы выводимы слова вида 00..0011..1122..22, в которых
числа нулей, единиц и двоек равны, и только они.
13.1.3. Доказать, что не существует КС-грамматики, в которой
были бы выводимы слова вида 00..0011..1122..22, в которых
числа нулей, единиц и двоек равны, и только они.
Нетерминальный символ можно рассматривать как << родовое имя>> для выводимых из него слов. В следующем примере для наглядности в качестве нетерминальных символов использованы фрагменты русских слов, заключенные в угловые скобки. (С точки зрения грамматики каждый такой фрагмент -- один символ!)
 Согласно этой грамматике, выражение 32992 -- это
последовательность слагаемых 32993, разделенных плюсами,
слагаемое -- это последовательность множителей 32994,
разделенных звездочками (знаками умножения), а множитель -- это
либо буква x, либо выражение в скобках.
Согласно этой грамматике, выражение 32992 -- это
последовательность слагаемых 32993, разделенных плюсами,
слагаемое -- это последовательность множителей 32994,
разделенных звездочками (знаками умножения), а множитель -- это
либо буква x, либо выражение в скобках.
![]() 13.1.4. Приведите пример другой грамматики, задающей тот же
язык.
13.1.4. Приведите пример другой грамматики, задающей тот же
язык.
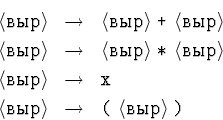 Эта грамматика хоть и проще, но в некоторых отношениях хуже, о
чем мы еще будем говорить.
Эта грамматика хоть и проще, но в некоторых отношениях хуже, о
чем мы еще будем говорить.
![]() 13.1.5. Дана произвольная КС-грамматика. Построить алгоритм
проверки принадлежности задаваемому ей языку, работающий
полиномиальное время (т.е. число действий не превосходит
полинома от длины проверяемого слова; полином может зависеть от
грамматики).
13.1.5. Дана произвольная КС-грамматика. Построить алгоритм
проверки принадлежности задаваемому ей языку, работающий
полиномиальное время (т.е. число действий не превосходит
полинома от длины проверяемого слова; полином может зависеть от
грамматики).
(1) Пусть в грамматике есть нетерминалы ![]() .Построим новую грамматику с нетерминалами
.Построим новую грамматику с нетерминалами ![]() так, чтобы выполнялось такое свойство: из Ki' выводятся (в
новой грамматике) те же слова, что из Ki в старой, за
исключением пустого слова, которое не выводится.
так, чтобы выполнялось такое свойство: из Ki' выводятся (в
новой грамматике) те же слова, что из Ki в старой, за
исключением пустого слова, которое не выводится.
Чтобы выполнить такое преобразование грамматики, надо выяснить, из каких нетерминалов исходной грамматики выводится пустое слово, а затем каждое правило заменить на совокупность правил, получающихся, если в правой части опустить какие-либо из нетерминалов, из которых выводится пустое слово, а у остальных поставить штрихи. Например, если в исходной грамматике было правило
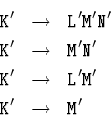
(2) Итак, мы свели дело к грамматике, где ни из одного нетерминала не выводится пустое слово. Теперь устраним << циклы>> вида
(3) Теперь проверка принадлежности какого-либо слова языку,
порожденному грамматикой, может выполняться так: для каждого
подслова проверяемого слова и для каждого нетерминала выясняем,
порождается ли это подслово этим нетерминалом. При этом подслова
проверяются в порядке возрастания длин, а нетерминалы -- в таком
порядке, чтобы при наличии правила ![]() нетерминал L
проверялся раньше нетерминала K . (Это возможно в силу отсутствия
циклов.) Поясним этот процесс на примере.
нетерминал L
проверялся раньше нетерминала K . (Это возможно в силу отсутствия
циклов.) Поясним этот процесс на примере.
Пусть в грамматике есть правила
Легко видеть, что число действий этого алгоритма
полиномиально. Степень полинома зависит от числа нетерминалов в
правых частях правил и может быть понижена, если грамматику
преобразовать к форме, в которой правая часть каждого правила
содержит 1 или 2 нетерминала (это легко сделать, вводя новые
нетерминалы: например, правило K ![]() LMK можно
заменить на K
LMK можно
заменить на K ![]() LN и N
LN и N ![]() MK, где
N -- новый нетерминал).
MK, где
N -- новый нетерминал).![]()
![]() 13.1.6. Рассмотрим грамматику с единственным нетерминалом
K, нетерминалами 1, 2, 3 и правилами
13.1.6. Рассмотрим грамматику с единственным нетерминалом
K, нетерминалами 1, 2, 3 и правилами
![]() 13.1.7. Тот же вопрос для грамматики
13.1.7. Тот же вопрос для грамматики