Пусть на множестве значений типа T фиксирован порядок.
Назовем T -дерево упорядоченным,
если выполнено такое свойство:
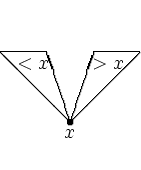
для любой вершины x все пометки в ее левом поддереве меньше
пометки в x , а все пометки в ее правом поддереве больше пометки
в x .
 12.1.1. Доказать, что в упорядоченном дереве все пометки
различны.
12.1.1. Доказать, что в упорядоченном дереве все пометки
различны.
[Указание. Индукция по высоте дерева.]
pvv
1/8/1999

![]() 12.1.1. Доказать, что в упорядоченном дереве все пометки
различны.
12.1.1. Доказать, что в упорядоченном дереве все пометки
различны.