Простейший пример

$\scriptstyle{\blacktriangleright}$ 10.1.1. Имеется последовательность символов ${\hbox{\tt x[1]}}\ldots{\hbox{\tt x[n]}}$ .Определить, имеются ли в ней идущие друг за другом символы abcd. (Другими словами, требуется выяснить, есть ли в слове ${\hbox{\tt x[1]}}\ldots{\hbox{\tt x[n]}}$ подслово abcd.)

Решение. Имеется примерно n (если быть точным, n-3) позиций, на которых может находиться искомое подслово в исходном слове. Для каждой из позиций можно проверить, действительно ли там оно находится, сравнив четыре символа. Однако есть более эффективный способ. Читая слово ${\hbox{\tt x[1]}}\ldots{\hbox{\tt x[n]}}$ слева направо, мы ожидаем появления буквы a. Как только она появилась, мы ищем за ней букву b, затем c, и, наконец, d. Если наши ожидания оправдываются, то слово abcd обнаружено. Если же какая-то из нужных букв не появляется, мы оказываемся у разбитого корыта и начинаем все сначала.

Этот простой алгоритм можно описать в разных терминах. Используя терминологию так называемых конечных автоматов, можно сказать, что при чтении слова x слева направо мы в каждый момент находимся в одном из следующих состояний: << начальное>> (0), << сразу после a>> (1), << сразу после ab>> (2), << сразу после abc>> (3) и << сразу после abcd>> (4). Читая очередную букву,

1cm

мы переходим в следующее состояние по правилу

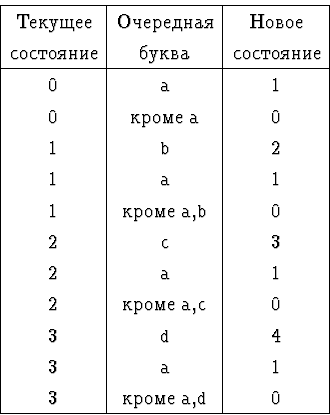
$\begin{displaymath} \begin{tabular} {\vert c\vert c\vert c\vert} \hline Текуще... ... кроме {\hbox{\tt a}},{\hbox{\tt d}} & 0 \\ \hline\end{tabular}\end{displaymath}$

Как только мы попадем в состояние 4, работа заканчивается.

Соответствующая программа очевидна (мы указываем новое состояние, даже если оно совпадает со старым; эти строки можно опустить):

        i:=1; state:=0;
        {i - первая непрочитанная буква, state - состояние}
        while (i <> n+1) and (state <> 4) do begin
        | if state = 0 then begin
        | | if x[i] = a then begin
        | | | state:= 1;
        | | end else begin
        | | | state:= 0;
        | | end;
        | end else if state = 1 then begin
        | | if x[i] = b then begin
        | | | state:= 2;
        | | end else if x[i] = a then begin
        | | | state:= 1;
        | | end else begin
        | | | state:= 0;
        | | end;
        | end else if state = 2 then begin
        | | if x[i] = c then begin
        | | | state:= 3;
        | | end else if x[i] = a then begin
        | | | state:= 1;
        | | end else begin
        | | | state:= 0;
        | | end;
        | end else if state = 3 then begin
        | | if x[i] = d then begin
        | | | state:= 4;
        | | end else if x[i] = a then begin
        | | | state:= 1;
        | | end else begin
        | | | state:= 0;
        | | end;
        | end;
        end;
        answer := (state = 4);

Иными словами, мы в каждый момент храним информацию о том, какое максимальное начало нашего образца abcd является концом прочитанной части. (Его длина и есть то << состояние>>, о котором шла речь.) $\scriptstyle\blacktriangleleft$

Терминология, нами используемая, такова. Слово -- это любая последовательность символов из некоторого фиксированного конечного множества. Это множество называется алфавитом, его элементы -- буквами. Если отбросить несколько букв с конца слова, останется другое слово, называемое началом первого. Любое слово также считается своим началом. Конец слова -- то, что останется, если отбросить несколько первых букв. Любое слово считается своим концом. Подслово -- то, что останется, если отбросить буквы и с начала, и с конца. (Другими словами, подслова -- это концы начал, или, что то же, начала концов.)

В терминах индуктивных функций (см. раздел 1.3) ситуацию можно описать так: рассмотрим функцию на словах, которая принимает два значения << истина>> и << ложь>> и истинна на словах, имеющих abcd своим подсловом. Эта функция не является индуктивной, но имеет индуктивное расширение $\begin{displaymath} \displaylines{ \qquad x \mapsto \hbox{длина максимального на... ...t abcd}},}\hfill\cr \hfill \hbox{являющегося концом $x$}\qquad}\end{displaymath}$

pvv
1/8/1999