 4.3.1. Найти количество различных чисел среди элементов данного
массива. Число действий порядка
4.3.1. Найти количество различных чисел среди элементов данного
массива. Число действий порядка 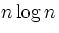 . (Эта задача уже была в
главе 1.)
. (Эта задача уже была в
главе 1.)
Решение. Отсортировать числа, а затем посчитать количество
различных, просматривая элементы массива по порядку.
 4.3.2. Дано n отрезков
4.3.2. Дано n отрезков ![$[{\hbox{\tt a[i]}},{\hbox{\tt b[i]}}]$](img261.gif) на прямой
(
на прямой
(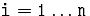 ). Найти максимальное k, для
которого существует точка прямой, покрытая k отрезками (<<
максимальное число слоев>>). Число действий -- порядка
). Найти максимальное k, для
которого существует точка прямой, покрытая k отрезками (<<
максимальное число слоев>>). Число действий -- порядка
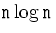 .
.
Решение. Упорядочим все левые и правые концы отрезков
вместе (при этом левый конец считается меньше правого конца,
расположенного в той же точке прямой). Далее двигаемся слева направо, считая число слоев. Встреченный левый конец увеличивает
число слоев на 1, правый -- уменьшает. Отметим, что примыкающие
друг к другу отрезки обрабатываются правильно: сначала идет
левый конец (правого отрезка), а затем -- правый (левого
отрезка).
 4.3.3. Дано n точек на плоскости. Указать (n-1) -звенную
несамопересекающуюся незамкнутую ломаную, проходящую через все
эти точки. (Соседним отрезкам ломаной разрешается лежать на
одной прямой.) Число действий порядка
4.3.3. Дано n точек на плоскости. Указать (n-1) -звенную
несамопересекающуюся незамкнутую ломаную, проходящую через все
эти точки. (Соседним отрезкам ломаной разрешается лежать на
одной прямой.) Число действий порядка 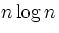 .
.
Решение. Упорядочим точки по x -координате, а при равных
x -координатах -- по y -координате. В таком порядке и можно
проводить ломаную.
 4.3.4. Та же задача, если ломаная должна быть замкнутой.
4.3.4. Та же задача, если ломаная должна быть замкнутой.
Решение. Возьмем самую левую точку (то есть точку с
наименьшей x -координатой) и проведем из нее лучи во все
остальные точки. Теперь упорядочим эти лучи снизу вверх,
а точки на одном
луче упорядочим по
расстоянию от начала луча (это делается для всех лучей, кроме
нижнего и верхнего).
Ломаная выходит из выбранной
(самой левой) точки по нижнему лучу, затем по всем остальным
лучам (в описанном порядке) и возвращается по верхнему лучу.
 4.3.5. Дано n точек на плоскости. Построить их выпуклую
оболочку -- минимальную выпуклую фигуру, их содержащую. (Резиновое
колечко, натянутое на вбитые в доску гвозди -- их выпуклая оболочка.)
Число операций не более
4.3.5. Дано n точек на плоскости. Построить их выпуклую
оболочку -- минимальную выпуклую фигуру, их содержащую. (Резиновое
колечко, натянутое на вбитые в доску гвозди -- их выпуклая оболочка.)
Число операций не более 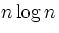 .
.
[Указание. Упорядочим точки -- годится любой из порядков,
использованных в двух предыдущих задачах. Затем, рассматривая
точки по очереди, будем строить выпуклую оболочку уже
рассмотренных точек. (Для хранения выпуклой оболочки полезно
использовать дек, см. главу 6. Впрочем, при
упорядочении точек по углам это излишне.)]
pvv
1/8/1999
![]() 4.3.1. Найти количество различных чисел среди элементов данного
массива. Число действий порядка
4.3.1. Найти количество различных чисел среди элементов данного
массива. Число действий порядка ![]() . (Эта задача уже была в
главе 1.)
. (Эта задача уже была в
главе 1.)
![]() 4.3.2. Дано n отрезков
4.3.2. Дано n отрезков ![]() на прямой
(
на прямой
(![]() ). Найти максимальное k, для
которого существует точка прямой, покрытая k отрезками (<<
максимальное число слоев>>). Число действий -- порядка
). Найти максимальное k, для
которого существует точка прямой, покрытая k отрезками (<<
максимальное число слоев>>). Число действий -- порядка
![]() .
.
![]() 4.3.3. Дано n точек на плоскости. Указать (n-1) -звенную
несамопересекающуюся незамкнутую ломаную, проходящую через все
эти точки. (Соседним отрезкам ломаной разрешается лежать на
одной прямой.) Число действий порядка
4.3.3. Дано n точек на плоскости. Указать (n-1) -звенную
несамопересекающуюся незамкнутую ломаную, проходящую через все
эти точки. (Соседним отрезкам ломаной разрешается лежать на
одной прямой.) Число действий порядка ![]() .
.![]() 4.3.4. Та же задача, если ломаная должна быть замкнутой.
4.3.4. Та же задача, если ломаная должна быть замкнутой.
![]() 4.3.5. Дано n точек на плоскости. Построить их выпуклую
оболочку -- минимальную выпуклую фигуру, их содержащую. (Резиновое
колечко, натянутое на вбитые в доску гвозди -- их выпуклая оболочка.)
Число операций не более
4.3.5. Дано n точек на плоскости. Построить их выпуклую
оболочку -- минимальную выпуклую фигуру, их содержащую. (Резиновое
колечко, натянутое на вбитые в доску гвозди -- их выпуклая оболочка.)
Число операций не более ![]() .
.