![]() 4.2.1. Предложить алгоритм сортировки, число действий которого
было бы порядка
4.2.1. Предложить алгоритм сортировки, число действий которого
было бы порядка ![]() , то есть не превосходило бы
, то есть не превосходило бы ![]() для некоторого C и для всех n .
для некоторого C и для всех n .
Пусть k -- положительное целое число. Разобьем массив
![]() на отрезки длины k. (Первый --
на отрезки длины k. (Первый --
![]() , затем
, затем ![]() и
так далее.) Последний отрезок будет неполным, если n не делится
на k. Назовем массив k-упорядоченным, если каждый из
этих отрезков в отдельности
упорядочен. Любой массив 1-упорядочен. Если
массив k-упорядочен и
и
так далее.) Последний отрезок будет неполным, если n не делится
на k. Назовем массив k-упорядоченным, если каждый из
этих отрезков в отдельности
упорядочен. Любой массив 1-упорядочен. Если
массив k-упорядочен и ![]() , то он упорядочен.
, то он упорядочен.
Мы опишем, как преобразовать k-упорядоченный массив в 2k-упорядоченный (из тех же элементов). С помощью этого преобразования алгоритм записывается так:
k:=1;
{массив x является k-упорядоченным}
while k < n do begin
| ..преобразовать k-упорядоченный массив в 2k-упорядоченный;
| k := 2 * k;
end;
Требуемое преобразование состоит в том,что мы многократно
<< сливаем>> два упорядоченных отрезка длины не больше k в
один упорядоченный отрезок. Пусть процедура
![]() при
при ![]() сливает отрезки
сливает отрезки
![]() и
и ![]() в
упорядоченный отрезок
в
упорядоченный отрезок ![]() (не затрагивая
других частей массива x).
(не затрагивая
других частей массива x).
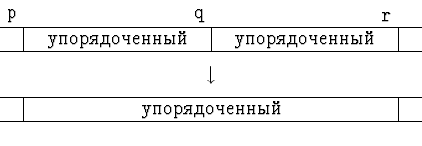 Тогда преобразование k-упорядоченного массива в
2k-упорядоченный
осуществляется так:
Тогда преобразование k-упорядоченного массива в
2k-упорядоченный
осуществляется так:
t:=0;
{t кратно 2k или t = n, x[1]..x[t] является
2k-упорядоченным; остаток массива x не изменился}
while t + k < n do begin
| p := t;
| q := t+k;
| ...r := min (t+2*k, n); {min(a,b) - минимум из a и b}
| слияние (p,q,r);
| t := r;
end;
Слияние требует вспомогательного массива для записи результатов
слияния -- обозначим его b. Через p0 и q0 обозначим номера
последних элементов участков, подвергшихся слиянию, s0
-- последний записанный в массив b элемент. На каждом шаге слияния
производится одно из двух действий:
b[s0+1]:=x[p0+1];
p0:=p0+1;
s0:=s0+1;
или
b[s0+1]:=x[q0+1];
q0:=q0+1;
s0:=s0+1;
Первое действие (взятие элемента из первого отрезка) может
производиться при одновременном выполнении двух условий:
(1) первый отрезок не кончился ( (2) второй отрезок кончился (![]() ) или не
кончился, но элемент в нем не меньше очередного элемента первого
отрезка [
) или не
кончился, но элемент в нем не меньше очередного элемента первого
отрезка [![]() ) и
(
) и
(![]() )].
)].
Аналогично для второго действия. Итак, получаем
p0 := p; q0 := q; s0 := p;
while (p0 <> q) or (q0 <> r) do begin
| if (p0 < q) and ((q0 = r) or ((q0 < r) and
| | (x[p0+1] <= x[q0+1]))) then begin
| | b [s0+1] := x [p0+1];
| | p0 := p0+1;
| | s0 := s0+1;
| end else begin
| | {(q0 < r) and ((p0 = q) or ((p0<q) and
| | (x[p0+1] >= x[q0+1])))}
| | b [s0+1] := x [q0+1];
| | q0 := q0 + 1;
| | s0 := s0 + 1;
| end;
end;
(Если оба отрезка не кончены и первые невыбранные элементы в них
равны, то допустимы оба действия; в программе выбрано первое.)
Остается лишь переписать результат слияния обратно в массив x.
Программа имеет привычный дефект: обращение к несуществующим элементам массива при вычислении булевских выражений.
Нарисуем << полное двоичное дерево>> -- картинку, в которой снизу один кружок, из него выходят стрелки в два других, из каждого -- в два других и так далее:

Будем говорить, что стрелки ведут << от отцов к
сыновьям>>: у каждого кружка два сына и один отец (если кружок
не в самом верху или низу).
Предположим для простоты, что количество подлежащих
сортировке чисел есть степень двойки, и они могут заполнить один
из рядов целиком. Запишем их туда. Затем заполним часть дерева
под ними по правилу:
![]() Тем самым в корне дерева (нижнем кружке) будет записано
минимальное число во всем массиве.
Тем самым в корне дерева (нижнем кружке) будет записано
минимальное число во всем массиве.
Изымем из сортируемого массива минимальный элемент. Для
этого его надо вначале найти. Это можно сделать, идя от корня:
от отца переходим к тому сыну, где записано то же число. Изъяв
минимальный элемент, заменим его символом ![]() и
скорректируем более низкие ярусы (для этого надо снова пройти
путь к корню). При этом считаем, что
и
скорректируем более низкие ярусы (для этого надо снова пройти
путь к корню). При этом считаем, что ![]() .Тогда в корне появится второй по величине
элемент, мы изымаем его, заменяя бесконечностью и корректируя
дерево. Так постепенно мы изымем все элементы в порядке
возрастания, пока в корне не останется бесконечность.
.Тогда в корне появится второй по величине
элемент, мы изымаем его, заменяя бесконечностью и корректируя
дерево. Так постепенно мы изымем все элементы в порядке
возрастания, пока в корне не останется бесконечность.
При записи этого алгоритма полезно нумеровать кружки
числами ![]() -- при этом
сыновьями кружка номер n
являются кружки 2n и
-- при этом
сыновьями кружка номер n
являются кружки 2n и ![]() . Подробное изложение
этого алгоритма мы опустим, поскольку мы изложим более
эффективный вариант, не требующий дополнительной памяти, кроме
конечного числа переменных (в дополнение к сортируемому массиву).
. Подробное изложение
этого алгоритма мы опустим, поскольку мы изложим более
эффективный вариант, не требующий дополнительной памяти, кроме
конечного числа переменных (в дополнение к сортируемому массиву).
Мы будем записывать сортируемые числа во всех вершинах
дерева, а не только на верхнем уровне. Пусть
![]() -- массив, подлежащий сортировке.
Вершинами дерева будут числа от 1 до n; о числе x[i] мы будем
говорить как о числе, стоящем в вершине i. В процессе сортировки
количество вершин дерева будет сокращаться. Число вершин
текущего дерева будем хранить в переменной k. Таким образом, в
процессе работы алгоритма массив
-- массив, подлежащий сортировке.
Вершинами дерева будут числа от 1 до n; о числе x[i] мы будем
говорить как о числе, стоящем в вершине i. В процессе сортировки
количество вершин дерева будет сокращаться. Число вершин
текущего дерева будем хранить в переменной k. Таким образом, в
процессе работы алгоритма массив ![]() делится на две части: в
делится на две части: в ![]() хранятся числа
на дереве, а в
хранятся числа
на дереве, а в ![]() хранится уже
отсортированная в порядке возрастания часть массива -- элементы,
уже занявшие свое законное место.
хранится уже
отсортированная в порядке возрастания часть массива -- элементы,
уже занявшие свое законное место.
На каждом шаге алгоритм будет изымать максимальный элемент дерева и помещать его в отсортированную часть, на освободившееся в результате сокращения дерева место.
Договоримся о терминологии. Вершинами дерева считаются
числа от 1 до текущего значения переменной k. У каждой
вершины s могут быть сыновья 2s и 2s+1. Если оба
этих числа больше k, то сыновей нет; такая вершина
называется листом. Если ![]() , то вершина s имеет
ровно одного сына (2s).
, то вершина s имеет
ровно одного сына (2s).
Для каждого s из ![]() рассмотрим
<< поддерево>> с корнем в s: оно содержит вершину s и
всех ее потомков (сыновей, внуков и так далее -- до
тех пор, пока мы не выйдем из отрезка
рассмотрим
<< поддерево>> с корнем в s: оно содержит вершину s и
всех ее потомков (сыновей, внуков и так далее -- до
тех пор, пока мы не выйдем из отрезка ![]() ).
Вершину s будем называть регулярной, если стоящее в ней
число -- максимальный элемент s-поддерева; s-поддерево
назовем регулярным, если все его вершины регулярны. (В
частности, любой лист образует регулярное одноэлементное
поддерево.)
).
Вершину s будем называть регулярной, если стоящее в ней
число -- максимальный элемент s-поддерева; s-поддерево
назовем регулярным, если все его вершины регулярны. (В
частности, любой лист образует регулярное одноэлементное
поддерево.)
Схема алгоритма такова:
k:= n
... Сделать 1-поддерево регулярным;
{x[1],..,x[k] <= x[k+1] <=..<= x[n]; 1-поддерево регулярно,
в частности, x[1] - максимальный элемент среди x[1]..x[k]}
while k <> 1 do begin
| ... обменять местами x[1] и x[k];
| k := k - 1;
| {x[1]..x[k-1] <= x[k] <=...<= x[n]; 1-поддерево регу-
| лярно везде, кроме, возможно, самого корня }
| ... восстановить регулярность 1-поддерева всюду
end;
В качестве вспомогательной процедуры нам понадобится процедура
восстановления регулярности s-поддерева в корне. Вот она:
{s-поддерево регулярно везде, кроме, возможно, корня}
t := s;
{s-поддерево регулярно везде, кроме, возможно, вершины t}
while ((2*t+1 <= k) and (x[2*t+1] > x[t])) or
| ((2*t <= k) and (x[2*t] > x[t])) do begin
| if (2*t+1 <= k) and (x[2*t+1] >= x[2*t]) then begin
| | ... обменять x[t] и x[2*t+1];
| | t := 2*t + 1;
| end else begin
| | ... обменять x[t] и x[2*t];
| | t := 2*t;
| end;
end;
Чтобы убедиться в правильности этой процедуры, посмотрим на нее повнимательнее. Пусть в s-поддереве все вершины, кроме разве что вершины t, регулярны. Рассмотрим сыновей вершины t. Они регулярны, и потому содержат наибольшие числа в своих поддеревьях. Таким образом, на роль наибольшего числа в t-поддереве могут претендовать число в самой вершине t и числа в ее сыновьях. (В первом случае вершина t регулярна, и все в порядке.) В этих терминах цикл можно записать так:
while наибольшее число не в t, а в одном из сыновей do begin
| if оно в правом сыне then begin
| | поменять t с ее правым сыном; t:= правый сын
| end else begin {наибольшее число - в левом сыне}
| | поменять t с ее левым сыном; t:= левый сын
| end
end
После обмена вершина t становится регулярной (в нее попадает
максимальное число t-поддерева). Не принявший участия в
обмене сын остается регулярным, а принявший участие может и не
быть регулярным. В остальных вершинах s-поддерева не изменились
ни числа, ни поддеревья их потомков (разве что два элемента
поддерева переставились), так что регулярность не нарушилась.
Эта же процедура может использоваться для того, чтобы сделать
1-поддерево регулярным на начальной стадии сортировки:
k := n;
u := n;
{все s-поддеревья с s>u регулярны }
while u<>0 do begin
| {u-поддерево регулярно везде, кроме разве что корня}
| ... восстановить регулярность u-поддерева в корне;
| u:=u-1;
end;
Теперь запишем процедуру сортировки на паскале (предполагая, что n -- константа, x имеет тип arr = array [1..n] of integer).
procedure sort (var x: arr); | var u, k: integer; | procedure exchange(i, j: integer); | | var tmp: integer; | | begin | | tmp := x[i]; | | x[i] := x[j]; | | x[j] := tmp; | end; | procedure restore (s: integer); | | var t: integer; | | begin | | t:=s; | | while ((2*t+1 <= k) and (x[2*t+1] > x[t])) or | | | ((2*t <= k) and (x[2*t] > x[t])) do begin | | | if (2*t+1 <= k) and (x[2*t+1] >= x[2*t]) then begin | | | | exchange (t, 2*t+1); | | | | t := 2*t+1; | | | end else begin | | | | exchange (t, 2*t); | | | | t := 2*t; | | | end; | | end; | end; begin | k:=n; | u:=n; | while u <> 0 do begin | | restore (u); | | u := u - 1; | end; | while k <> 1 do begin | | exchange (1, k); | | k := k - 1; | | restore (1); | end; end;`
Несколько замечаний
Метод, использованный при сортировке деревом, бывает полезным в других случах. (См. в главе 6 (о типах данных) об очереди с приоритетами.)
Сортировка слиянием хороша тем, что она на требует, чтобы весь сортируемый массив помещался в оперативной памяти. Можно сначала отсортировать такие куски, которые помещаются в памяти (например, с помощью дерева), а затем сливать полученные файлы.
Еще один практически важный алгоритм сортировки
(быстрая сортировка Хоара)
таков:
чтобы отсортировать массив, выберем случайный его элемент b , и
разобьем массив на три части: меньшие b , равные b и большие b . (Эта задача приведена в главе 1.) Теперь осталось
отсортировать первую и третью части: это делается тем же
способом. Время работы этого алгоритма -- случайная величина;
можно доказать, что в среднем он работает не больше ![]() .На практике -- он один из самых быстрых. (Мы еще вернемся к нему,
приведя его рекурсивную и нерекурсивную реализации.)
.На практике -- он один из самых быстрых. (Мы еще вернемся к нему,
приведя его рекурсивную и нерекурсивную реализации.)
Наконец, отметим, что сортировка за время порядка ![]() может быть выполнена с помощью техники сбалансированных деревьев
(см. главу 12), однако программы тут сложнее и
константа C довольно велика.
может быть выполнена с помощью техники сбалансированных деревьев
(см. главу 12), однако программы тут сложнее и
константа C довольно велика.